Question Number 116226 by bobhans last updated on 02/Oct/20
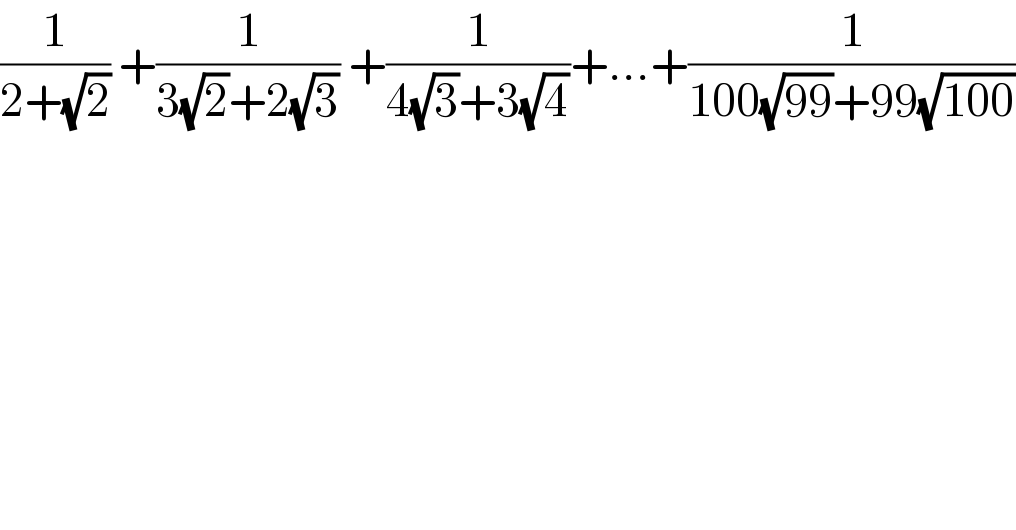
$$\frac{\mathrm{1}}{\mathrm{2}+\sqrt{\mathrm{2}}}\:+\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{2}}+\mathrm{2}\sqrt{\mathrm{3}}}\:+\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{3}}+\mathrm{3}\sqrt{\mathrm{4}}}+…+\frac{\mathrm{1}}{\mathrm{100}\sqrt{\mathrm{99}}+\mathrm{99}\sqrt{\mathrm{100}}} \\ $$
Commented by bemath last updated on 02/Oct/20

$$\mathrm{0}.\mathrm{9} \\ $$
Answered by john santu last updated on 02/Oct/20
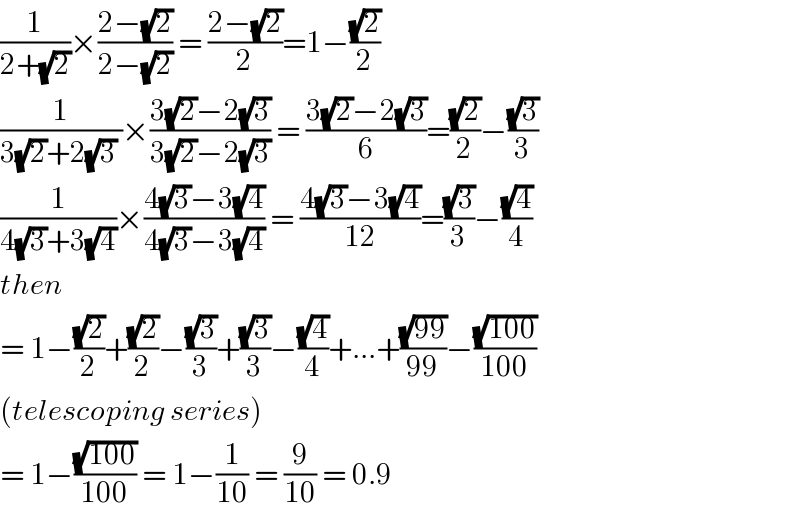
$$\frac{\mathrm{1}}{\mathrm{2}+\sqrt{\mathrm{2}}}×\frac{\mathrm{2}−\sqrt{\mathrm{2}}}{\mathrm{2}−\sqrt{\mathrm{2}}}\:=\:\frac{\mathrm{2}−\sqrt{\mathrm{2}}}{\mathrm{2}}=\mathrm{1}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{2}}+\mathrm{2}\sqrt{\mathrm{3}}\:}×\frac{\mathrm{3}\sqrt{\mathrm{2}}−\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}\sqrt{\mathrm{2}}−\mathrm{2}\sqrt{\mathrm{3}}}\:=\:\frac{\mathrm{3}\sqrt{\mathrm{2}}−\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{6}}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{3}}+\mathrm{3}\sqrt{\mathrm{4}}}×\frac{\mathrm{4}\sqrt{\mathrm{3}}−\mathrm{3}\sqrt{\mathrm{4}}}{\mathrm{4}\sqrt{\mathrm{3}}−\mathrm{3}\sqrt{\mathrm{4}}}\:=\:\frac{\mathrm{4}\sqrt{\mathrm{3}}−\mathrm{3}\sqrt{\mathrm{4}}}{\mathrm{12}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}−\frac{\sqrt{\mathrm{4}}}{\mathrm{4}} \\ $$$${then}\: \\ $$$$=\:\mathrm{1}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}−\frac{\sqrt{\mathrm{4}}}{\mathrm{4}}+…+\frac{\sqrt{\mathrm{99}}}{\mathrm{99}}−\frac{\sqrt{\mathrm{100}}}{\mathrm{100}} \\ $$$$\left({telescoping}\:{series}\right) \\ $$$$=\:\mathrm{1}−\frac{\sqrt{\mathrm{100}}}{\mathrm{100}}\:=\:\mathrm{1}−\frac{\mathrm{1}}{\mathrm{10}}\:=\:\frac{\mathrm{9}}{\mathrm{10}}\:=\:\mathrm{0}.\mathrm{9} \\ $$
Answered by Dwaipayan Shikari last updated on 02/Oct/20
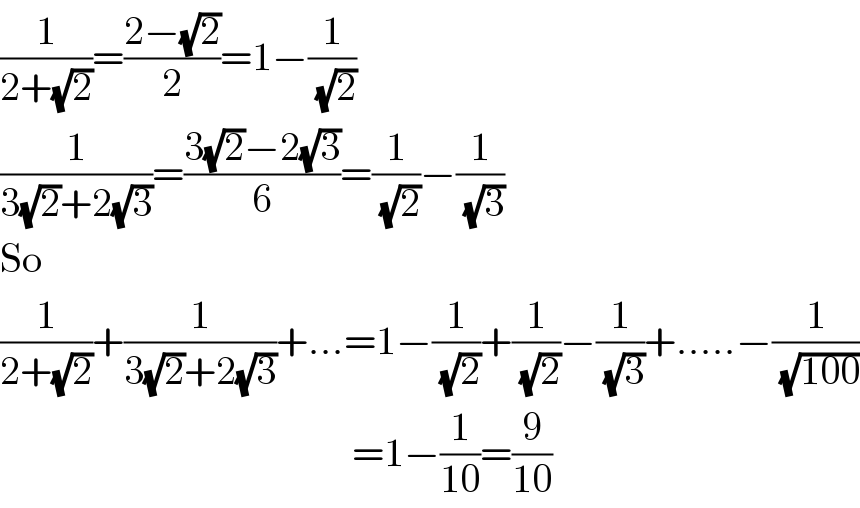
$$\frac{\mathrm{1}}{\mathrm{2}+\sqrt{\mathrm{2}}}=\frac{\mathrm{2}−\sqrt{\mathrm{2}}}{\mathrm{2}}=\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{2}}+\mathrm{2}\sqrt{\mathrm{3}}}=\frac{\mathrm{3}\sqrt{\mathrm{2}}−\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{6}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$$\mathrm{So} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}+\sqrt{\mathrm{2}}}+\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{2}}+\mathrm{2}\sqrt{\mathrm{3}}}+…=\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}+…..−\frac{\mathrm{1}}{\:\sqrt{\mathrm{100}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{10}}=\frac{\mathrm{9}}{\mathrm{10}} \\ $$
