Question Number 161800 by mathlove last updated on 22/Dec/21
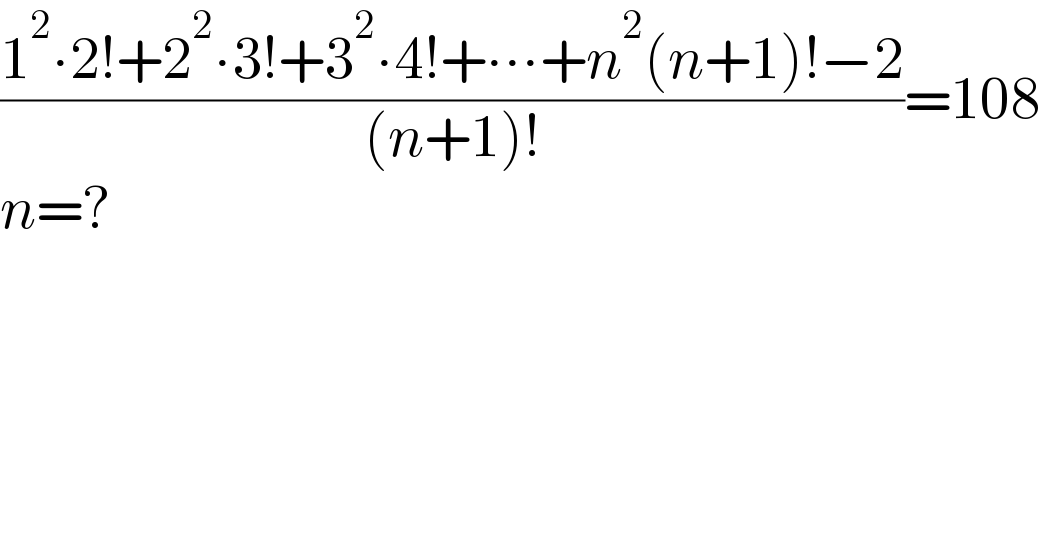
$$\frac{\mathrm{1}^{\mathrm{2}} \centerdot\mathrm{2}!+\mathrm{2}^{\mathrm{2}} \centerdot\mathrm{3}!+\mathrm{3}^{\mathrm{2}} \centerdot\mathrm{4}!+\centerdot\centerdot\centerdot+{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)!−\mathrm{2}}{\left({n}+\mathrm{1}\right)!}=\mathrm{108} \\ $$$${n}=? \\ $$
Commented by Rasheed.Sindhi last updated on 22/Dec/21

$${n}=\mathrm{10} \\ $$
Commented by mathlove last updated on 23/Dec/21

$${how}\:{solve}? \\ $$
Answered by Rasheed.Sindhi last updated on 24/Dec/21

$$\frac{\mathrm{1}^{\mathrm{2}} \centerdot\mathrm{2}!+\mathrm{2}^{\mathrm{2}} \centerdot\mathrm{3}!+\mathrm{3}^{\mathrm{2}} \centerdot\mathrm{4}!+\centerdot\centerdot\centerdot+{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)!−\mathrm{2}}{\left({n}+\mathrm{1}\right)!}=\mathrm{108} \\ $$$$\mathrm{LHS}\:\mathrm{can}\:\mathrm{be}\:\mathrm{proved}\:\mathrm{to}\:\mathrm{be}\:\mathrm{equal}\:\mathrm{to} \\ $$$$\mathrm{n}^{\mathrm{2}} +\mathrm{n}−\mathrm{2}\: \\ $$$$\left({For}\:{the}\:{proof}\:{see}\:{Q}#\mathrm{161860}\:\&\:\right. \\ $$$$\left.{Q}#\mathrm{161861}\right) \\ $$$$\:\:\therefore\:\:\:\:\:\:\:\:\mathrm{n}^{\mathrm{2}} +\mathrm{n}−\mathrm{2}=\mathrm{108} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{n}^{\mathrm{2}} +\mathrm{n}−\mathrm{110}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{n}−\mathrm{10}\right)\left(\mathrm{n}+\mathrm{11}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{n}=\mathrm{10}\:\:\mid\:\:\:\mathrm{n}=−\mathrm{11}\left(\mathrm{rejeted}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\: \\ $$
Commented by Rasheed.Sindhi last updated on 24/Dec/21

$${Q}#\mathrm{161861} \\ $$
