Question Number 176054 by BaliramKumar last updated on 11/Sep/22

$$\frac{\mathrm{1}}{\mathrm{2}!}\:+\:\frac{\mathrm{2}}{\mathrm{3}!}\:+\:\frac{\mathrm{3}}{\mathrm{4}!}\:+\:\frac{\mathrm{4}}{\mathrm{5}!}\:+\:………….\:\infty\:=\:? \\ $$
Answered by Ar Brandon last updated on 11/Sep/22
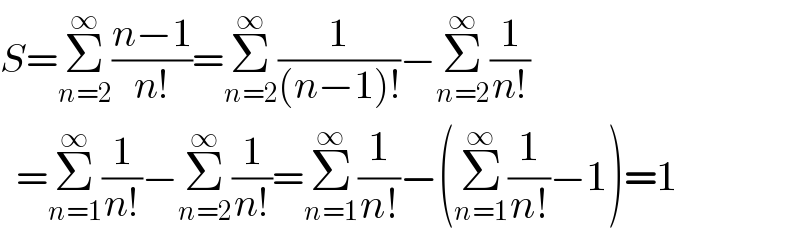
$${S}=\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{{n}−\mathrm{1}}{{n}!}=\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}−\mathrm{1}\right)!}−\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!} \\ $$$$\:\:=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}−\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}−\left(\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}−\mathrm{1}\right)=\mathrm{1} \\ $$
