Question Number 126617 by Khalmohmmad last updated on 22/Dec/20
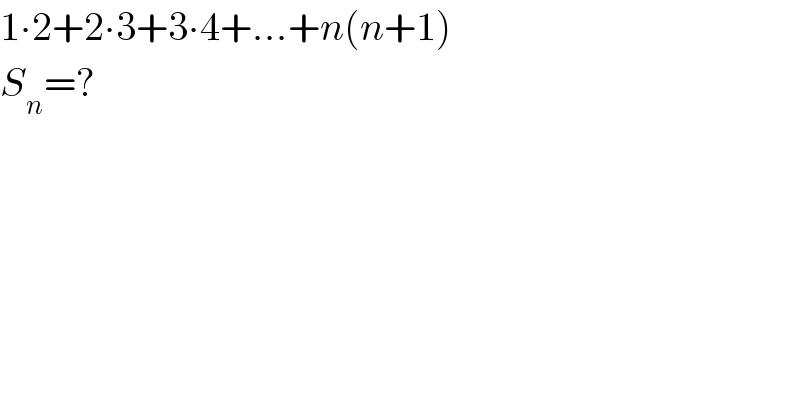
$$\mathrm{1}\centerdot\mathrm{2}+\mathrm{2}\centerdot\mathrm{3}+\mathrm{3}\centerdot\mathrm{4}+…+{n}\left({n}+\mathrm{1}\right) \\ $$$${S}_{{n}} =? \\ $$
Answered by Dwaipayan Shikari last updated on 22/Dec/20
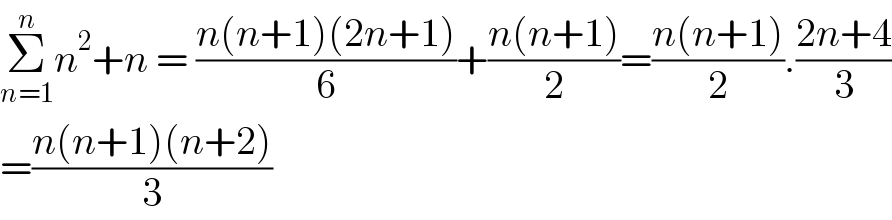
$$\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}{n}^{\mathrm{2}} +{n}\:=\:\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}}+\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}=\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}.\frac{\mathrm{2}{n}+\mathrm{4}}{\mathrm{3}} \\ $$$$=\frac{{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}{\mathrm{3}} \\ $$
Commented by JDamian last updated on 22/Dec/20
$${Review}\:{the}\:{sum}\:{index} \\ $$
Answered by Bird last updated on 23/Dec/20
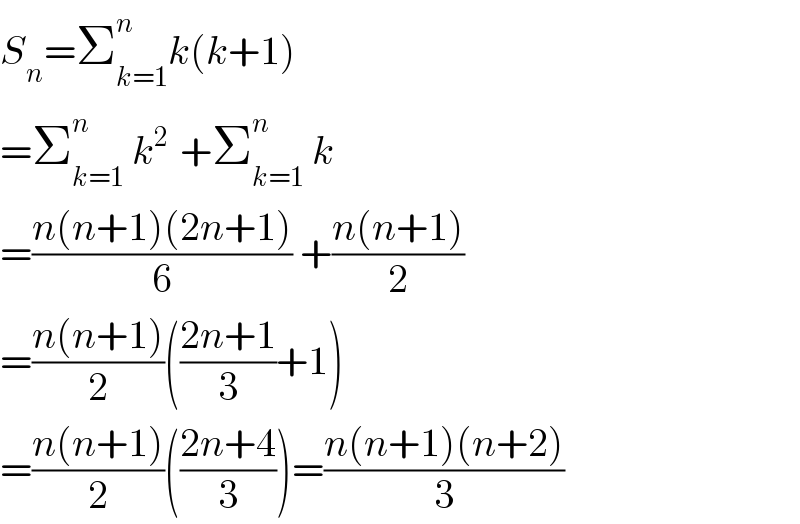
$${S}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} {k}\left({k}+\mathrm{1}\right) \\ $$$$=\sum_{{k}=\mathrm{1}} ^{{n}} \:{k}^{\mathrm{2}\:} \:+\sum_{{k}=\mathrm{1}} ^{{n}} \:{k} \\ $$$$=\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}}\:+\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$$=\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}\left(\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{3}}+\mathrm{1}\right) \\ $$$$=\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}\left(\frac{\mathrm{2}{n}+\mathrm{4}}{\mathrm{3}}\right)=\frac{{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}{\mathrm{3}} \\ $$
