Question Number 30245 by .none. last updated on 19/Feb/18
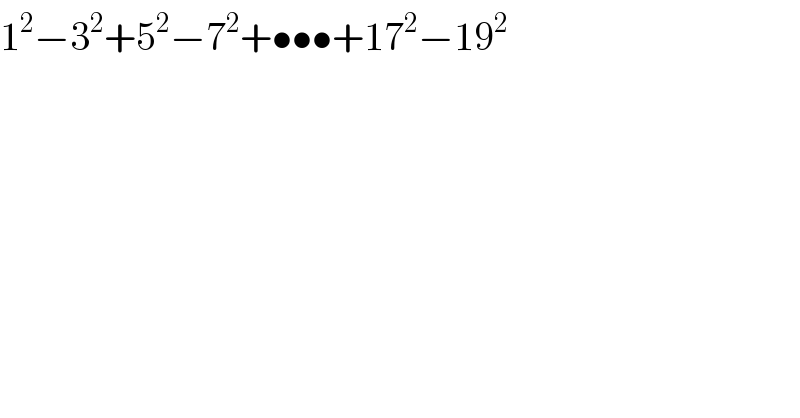
$$\mathrm{1}^{\mathrm{2}} −\mathrm{3}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} −\mathrm{7}^{\mathrm{2}} +\bullet\bullet\bullet+\mathrm{17}^{\mathrm{2}} −\mathrm{19}^{\mathrm{2}} \\ $$
Commented by Penguin last updated on 19/Feb/18
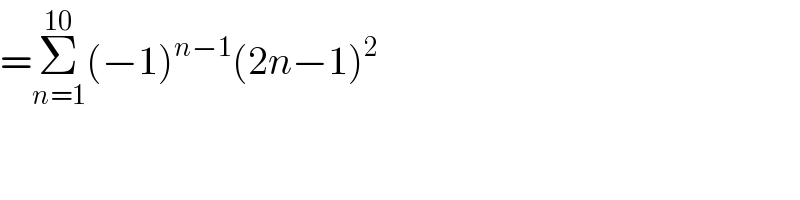
$$=\underset{{n}=\mathrm{1}} {\overset{\mathrm{10}} {\sum}}\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} \\ $$
Commented by abdo imad last updated on 20/Feb/18

$${let}\:{put}\:{S}_{{N}} \left({x}\right)=\sum_{{n}=\mathrm{1}} ^{{N}} \left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} {x}^{{n}} \:\:\:{and}\:{xfrom}\:{R}\:−\left\{\mathrm{1}\right\} \\ $$$${S}_{{N}} \left({x}\right)=\sum_{{n}=\mathrm{1}} ^{{N}} \left(\mathrm{4}{n}^{\mathrm{2}} \:−\mathrm{4}{n}\:+\mathrm{1}\right){x}^{{n}} \\ $$$$=\mathrm{4}\sum_{{n}=\mathrm{1}} ^{{N}} {n}^{\mathrm{2}} {x}^{{n}} \:−\mathrm{4}\sum_{{n}=} ^{{N}} \:{n}\:{x}^{{n}} \:+\:\sum_{{n}=\mathrm{1}} ^{{N}} \:{x}^{{n}} \\ $$$$=\mathrm{4}{A}_{{n}} \left({x}\right)\:−\mathrm{4}{B}_{{n}} \left({x}\right)\:+{C}_{{n}} \left({x}\right)\:{we}\:{have} \\ $$$${C}_{{n}} \left({x}\right)={x}\:\sum_{{n}=\mathrm{1}} ^{{N}} {x}^{{n}−\mathrm{1}} ={x}\sum_{{n}=\mathrm{0}} ^{{N}−\mathrm{1}} \:{x}^{{n}} ={x}\:\frac{\mathrm{1}−{x}^{{N}} }{\mathrm{1}−{x}} \\ $$$$\Rightarrow\frac{{dC}_{{n}} \left({x}\right)}{{dx}}=\:\frac{{d}}{{dx}}\left(\frac{{x}−{x}^{{N}+\mathrm{1}} }{\mathrm{1}−{x}}\right)=\sum_{{n}=\mathrm{1}} ^{{N}} {nx}^{{n}−\mathrm{1}} =\frac{{B}_{{n}} \left({x}\right)}{{x}}\:\Rightarrow \\ $$$${B}_{{n}} \left({x}\right)={x}\:\frac{{d}}{{dx}}\left(\:\frac{{x}\:−{x}^{{N}+\mathrm{1}} }{\mathrm{1}−{x}}\right)={x}\:\frac{\left(\mathrm{1}−\left({N}+\mathrm{1}\right){x}^{{N}} \:+\left({x}−{x}^{{N}+\mathrm{1}} \right)\right.}{\left(\mathrm{1}−{x}^{} \right)^{\mathrm{2}} }… \\ $$$${also}\:\frac{{dB}_{{n}} \left({x}\right)}{{dx}}=\sum_{{n}=\mathrm{1}} ^{{N}} {n}^{\mathrm{2}} \:{x}^{{n}−\mathrm{1}} =\frac{\mathrm{1}}{{x}}\sum_{{n}=\mathrm{1}} ^{{N}} {n}^{\mathrm{2}} {x}^{{n}} \:\Rightarrow \\ $$$${A}_{{n}} \left({x}\right)={x}\:\frac{{dB}_{{n}} \left({x}\right)}{{dx}}\:…{after}\:{finding}\:{A}_{{n}} \:,{B}_{{n}} ,{C}_{{n}} \:{take}\:{x}=−\mathrm{1} \\ $$$${and}\:{N}=\mathrm{20}\:…. \\ $$$$ \\ $$
Commented by abdo imad last updated on 20/Feb/18

$${N}=\mathrm{10}. \\ $$
Answered by ajfour last updated on 20/Feb/18
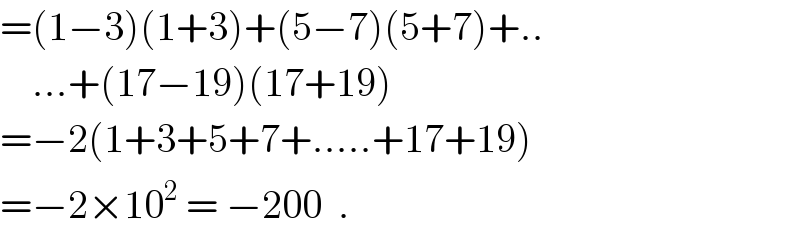
$$=\left(\mathrm{1}−\mathrm{3}\right)\left(\mathrm{1}+\mathrm{3}\right)+\left(\mathrm{5}−\mathrm{7}\right)\left(\mathrm{5}+\mathrm{7}\right)+.. \\ $$$$\:\:\:\:…+\left(\mathrm{17}−\mathrm{19}\right)\left(\mathrm{17}+\mathrm{19}\right) \\ $$$$=−\mathrm{2}\left(\mathrm{1}+\mathrm{3}+\mathrm{5}+\mathrm{7}+…..+\mathrm{17}+\mathrm{19}\right) \\ $$$$=−\mathrm{2}×\mathrm{10}^{\mathrm{2}} \:=\:−\mathrm{200}\:\:. \\ $$
Commented by abdo imad last updated on 20/Feb/18
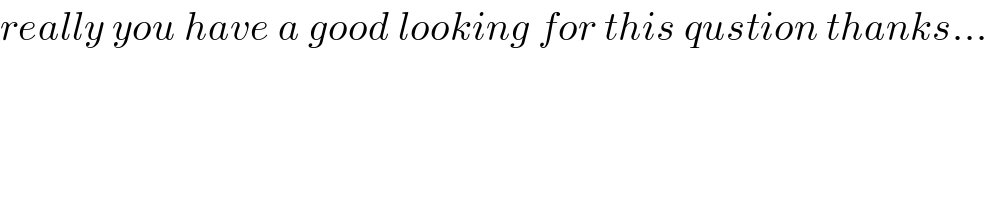
$${really}\:{you}\:{have}\:{a}\:{good}\:{looking}\:{for}\:{this}\:{qustion}\:{thanks}… \\ $$
