Menu Close

1-2-3-4-100-

Tinku Tara 0 Comments
Pin




Question Number 128112 by AgnibhoMukhopadhyay last updated on 04/Jan/21
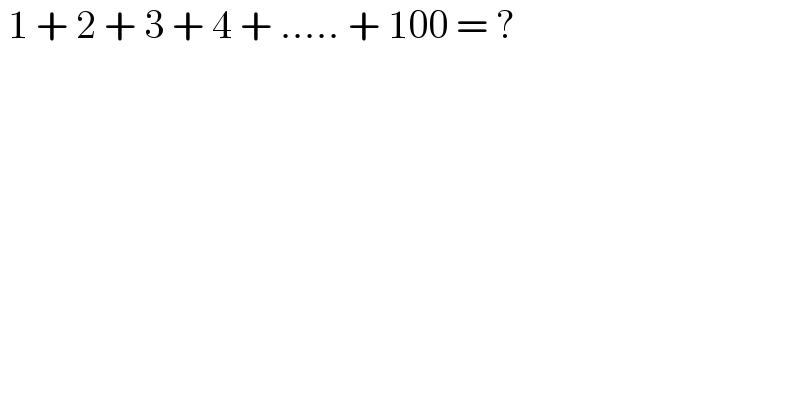
1 + 2 + 3 + 4 + ..... + 100 = ?
$$\:\mathrm{1}\:+\:\mathrm{2}\:+\:\mathrm{3}\:+\:\mathrm{4}\:+\:…..\:+\:\mathrm{100}\:=\:? \\ $$
Answered by Olaf last updated on 04/Jan/21
A (n+1)×(n+1) squared chess board contains (n+1)^2 squares. and : −Its diagonal contains n+1 squares −Its upper part contains n+(n−1)+ (n−2)+...+3+2+1 = S_n squares −Its lower part contains 1+2+3+...+ (n−2)+(n−1)+n = S_n squares ⇒ (n+1)^2 = (n+1)+2S_n ⇒ S_n = (((n+1)^2 −(n+1))/2) = ((n(n+1))/2)
$$\mathrm{A}\:\left({n}+\mathrm{1}\right)×\left({n}+\mathrm{1}\right)\:\mathrm{squared}\:\mathrm{chess}\:\mathrm{board} \\ $$$$\mathrm{contains}\:\left({n}+\mathrm{1}\right)^{\mathrm{2}} \:\mathrm{squares}. \\ $$$$ \\ $$$$\mathrm{and}\:: \\ $$$$ \\ $$$$−\mathrm{Its}\:\mathrm{diagonal}\:\mathrm{contains}\:{n}+\mathrm{1}\:\mathrm{squares} \\ $$$$−\mathrm{Its}\:\mathrm{upper}\:\mathrm{part}\:\mathrm{contains}\:{n}+\left({n}−\mathrm{1}\right)+ \\ $$$$\left({n}−\mathrm{2}\right)+…+\mathrm{3}+\mathrm{2}+\mathrm{1}\:=\:\mathrm{S}_{{n}} \:\mathrm{squares} \\ $$$$−\mathrm{Its}\:\mathrm{lower}\:\mathrm{part}\:\mathrm{contains}\:\mathrm{1}+\mathrm{2}+\mathrm{3}+…+ \\ $$$$\left({n}−\mathrm{2}\right)+\left({n}−\mathrm{1}\right)+{n}\:=\:\mathrm{S}_{{n}} \:\mathrm{squares} \\ $$$$ \\ $$$$\Rightarrow\:\left({n}+\mathrm{1}\right)^{\mathrm{2}} \:=\:\left({n}+\mathrm{1}\right)+\mathrm{2S}_{{n}} \\ $$$$\Rightarrow\:\mathrm{S}_{{n}} \:=\:\frac{\left({n}+\mathrm{1}\right)^{\mathrm{2}} −\left({n}+\mathrm{1}\right)}{\mathrm{2}}\:=\:\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}} \\ $$
Answered by Ar Brandon last updated on 04/Jan/21
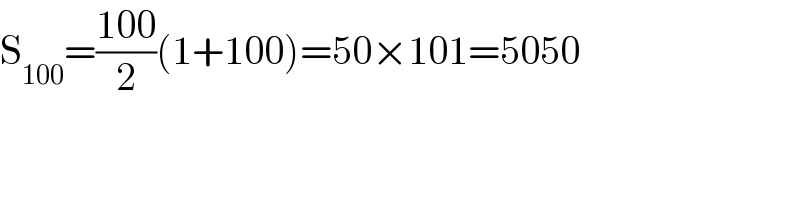
S_(100) =((100)/2)(1+100)=50×101=5050
$$\mathrm{S}_{\mathrm{100}} =\frac{\mathrm{100}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{100}\right)=\mathrm{50}×\mathrm{101}=\mathrm{5050} \\ $$
Answered by Geovanek last updated on 04/Jan/21
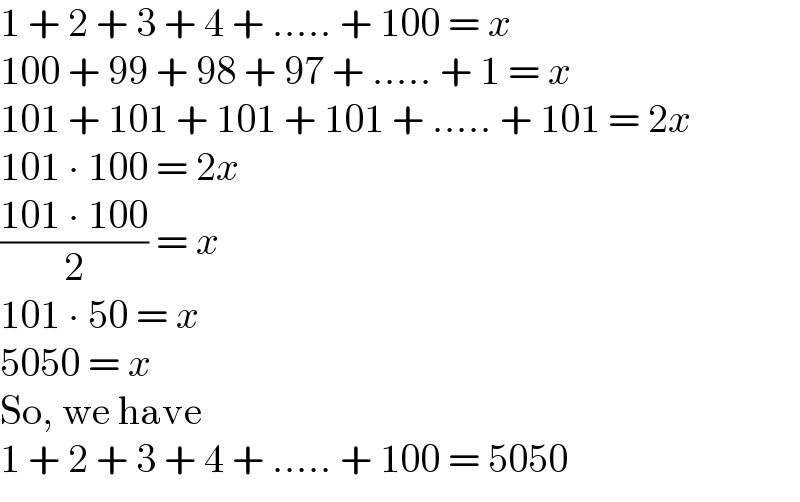
1 + 2 + 3 + 4 + ..... + 100 = x 100 + 99 + 98 + 97 + ..... + 1 = x 101 + 101 + 101 + 101 + ..... + 101 = 2x 101 ∙ 100 = 2x ((101 ∙ 100)/2) = x 101 ∙ 50 = x 5050 = x So, we have 1 + 2 + 3 + 4 + ..... + 100 = 5050
$$\mathrm{1}\:+\:\mathrm{2}\:+\:\mathrm{3}\:+\:\mathrm{4}\:+\:…..\:+\:\mathrm{100}\:=\:{x} \\ $$$$\mathrm{100}\:+\:\mathrm{99}\:+\:\mathrm{98}\:+\:\mathrm{97}\:+\:…..\:+\:\mathrm{1}\:=\:{x} \\ $$$$\mathrm{101}\:+\:\mathrm{101}\:+\:\mathrm{101}\:+\:\mathrm{101}\:+\:…..\:+\:\mathrm{101}\:=\:\mathrm{2}{x} \\ $$$$\mathrm{101}\:\centerdot\:\mathrm{100}\:=\:\mathrm{2}{x} \\ $$$$\frac{\mathrm{101}\:\centerdot\:\mathrm{100}}{\mathrm{2}}\:=\:{x} \\ $$$$\mathrm{101}\:\centerdot\:\mathrm{50}\:=\:{x} \\ $$$$\mathrm{5050}\:=\:{x} \\ $$$$\mathrm{So},\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{1}\:+\:\mathrm{2}\:+\:\mathrm{3}\:+\:\mathrm{4}\:+\:…..\:+\:\mathrm{100}\:=\:\mathrm{5050} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *