Question Number 100947 by bachamohamed last updated on 29/Jun/20

$$\sqrt{\mathrm{1}+\sqrt{\mathrm{2}+\sqrt{\mathrm{3}+\sqrt{\mathrm{4}+\sqrt{\mathrm{5}+…..\infty}}}}}=? \\ $$
Commented by bachamohamed last updated on 29/Jun/20
$$\mathrm{way}\:\mathrm{how}\:?\:\mathrm{solve}\:\mathrm{that} \\ $$
Commented by Dwaipayan Shikari last updated on 29/Jun/20
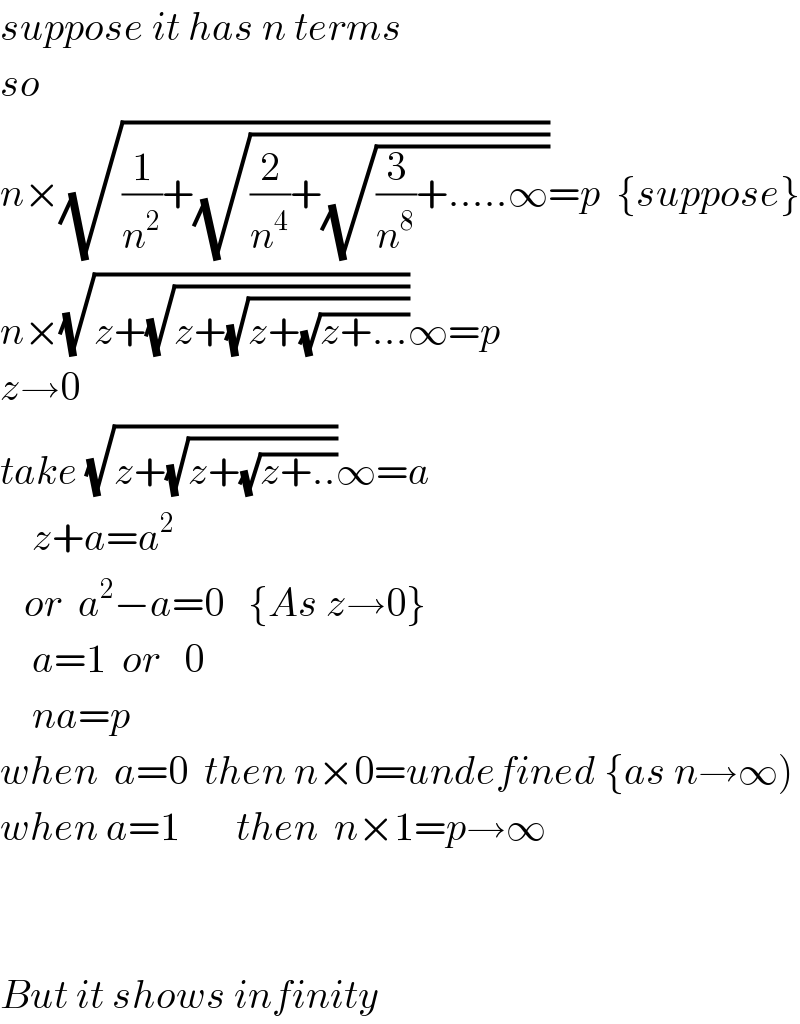
$${suppose}\:{it}\:{has}\:{n}\:{terms} \\ $$$${so} \\ $$$${n}×\sqrt{\frac{\mathrm{1}}{{n}^{\mathrm{2}} }+\sqrt{\frac{\mathrm{2}}{{n}^{\mathrm{4}} }+\sqrt{\frac{\mathrm{3}}{{n}^{\mathrm{8}} }+…..\infty}}}={p}\:\:\left\{{suppose}\right\} \\ $$$${n}×\sqrt{{z}+\sqrt{{z}+\sqrt{{z}+\sqrt{{z}+…}}}}\infty={p} \\ $$$${z}\rightarrow\mathrm{0} \\ $$$${take}\:\sqrt{{z}+\sqrt{{z}+\sqrt{{z}+..}}}\infty={a} \\ $$$$\:\:\:\:{z}+{a}={a}^{\mathrm{2}} \\ $$$$\:\:\:{or}\:\:{a}^{\mathrm{2}} −{a}=\mathrm{0}\:\:\:\left\{{As}\:{z}\rightarrow\mathrm{0}\right\} \\ $$$$\:\:\:\:{a}=\mathrm{1}\:\:{or}\:\:\:\mathrm{0} \\ $$$$\:\:\:\:{na}={p} \\ $$$${when}\:\:{a}=\mathrm{0}\:\:{then}\:{n}×\mathrm{0}={undefined}\:\left\{{as}\:{n}\rightarrow\infty\right) \\ $$$${when}\:{a}=\mathrm{1}\:\:\:\:\:\:\:{then}\:\:{n}×\mathrm{1}={p}\rightarrow\infty \\ $$$$ \\ $$$$ \\ $$$${But}\:{it}\:{shows}\:{infinity} \\ $$
