Question Number 100482 by Dwaipayan Shikari last updated on 26/Jun/20
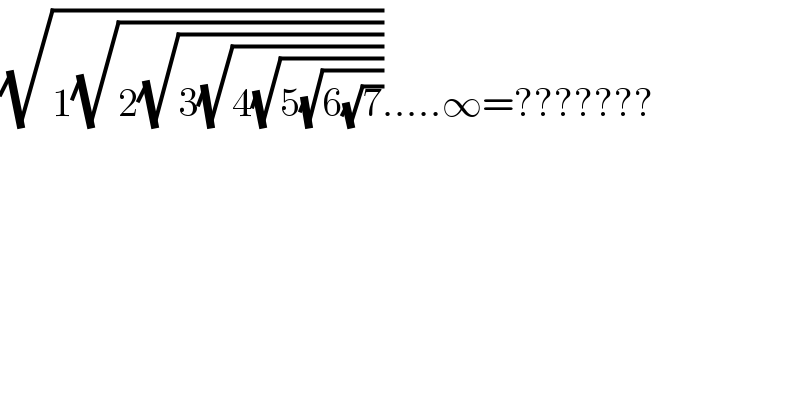
$$\sqrt{\mathrm{1}\sqrt{\mathrm{2}\sqrt{\mathrm{3}\sqrt{\mathrm{4}\sqrt{\mathrm{5}\sqrt{\mathrm{6}\sqrt{\mathrm{7}}}}}}}}…..\infty=??????? \\ $$
Answered by floor(10²Eta[1]) last updated on 27/Jun/20

$$\sqrt{\sqrt{\mathrm{1}.\mathrm{2}\sqrt{\mathrm{3}\sqrt{\mathrm{4}\sqrt{\mathrm{5}\sqrt{\mathrm{6}\sqrt{\mathrm{7}…\sqrt{{n}}}}}}}}} \\ $$$$\sqrt{\sqrt{\sqrt{\mathrm{1}.\mathrm{2}^{\mathrm{2}} .\mathrm{3}\sqrt{\mathrm{4}\sqrt{\mathrm{5}\sqrt{\mathrm{6}\sqrt{\mathrm{7}…\sqrt{{n}}}}}}}}} \\ $$$$\sqrt{\sqrt{\sqrt{\sqrt{\mathrm{1}.\mathrm{2}^{\mathrm{2}} .\mathrm{3}^{\mathrm{2}} .\mathrm{4}\sqrt{\mathrm{5}\sqrt{\mathrm{6}\sqrt{\mathrm{7}…\sqrt{{n}}}}}}}}} \\ $$$$…=^{\mathrm{2}^{{n}} } \sqrt{\mathrm{1}.\mathrm{2}^{\mathrm{2}} .\mathrm{3}^{\mathrm{2}} …\left({n}−\mathrm{1}\right)^{\mathrm{2}} {n}} \\ $$$$=^{\mathrm{2}^{{n}} } \sqrt{{n}!\left({n}−\mathrm{1}\right)!} \\ $$$${when}\:{you}\:{take}\:{the}\:{limit}\:{as}\:{n} \\ $$$${approaches}\:{infinite}\:{the}\:{result}\:{is}\:\mathrm{1} \\ $$$$\left({wolfram}\:{alpha}\right) \\ $$
Commented by bachamohamed last updated on 27/Jun/20

$${this}\:{solution}\:{is}\:{not}\:{correct}\:{because} \\ $$$${there}\:{is}\:{an}\:{error}\:{because}\: \\ $$$$\sqrt{\mathrm{1}\sqrt{\mathrm{2}\sqrt{\mathrm{3}\sqrt{\mathrm{4}\sqrt{\mathrm{5}\sqrt{…..}}}}}}\neq^{\mathrm{2}^{\mathrm{n}} } \sqrt{\mathrm{1}^{\mathrm{2}} .\mathrm{2}^{\mathrm{2}} .\mathrm{3}^{\mathrm{2}} ..\left({n}−\mathrm{1}\right)^{\mathrm{2}} {n}^{\mathrm{2}} } \\ $$$${but}\: \\ $$$$\sqrt{\mathrm{1}\sqrt{\mathrm{2}\sqrt{\mathrm{3}\sqrt{…\infty}}}}=^{\mathrm{2}^{{n}} } \sqrt{\mathrm{1}^{\mathrm{2}^{{n}−\mathrm{1}} } .\mathrm{2}^{\mathrm{2}^{{n}−\mathrm{2}} } .\mathrm{3}^{\mathrm{2}^{{n}−\mathrm{3}} } ….\left({n}−\mathrm{1}\right)^{\mathrm{2}^{} } .{n}} \\ $$
