Question Number 148154 by mathdanisur last updated on 25/Jul/21
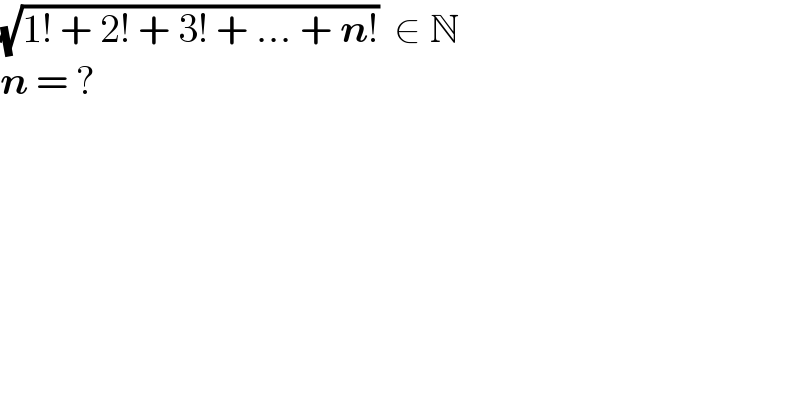
$$\sqrt{\mathrm{1}!\:+\:\mathrm{2}!\:+\:\mathrm{3}!\:+\:…\:+\:\boldsymbol{{n}}!}\:\:\in\:\mathbb{N} \\ $$$$\boldsymbol{{n}}\:=\:? \\ $$
Answered by puissant last updated on 25/Jul/21

$$\mathrm{n}=\mathrm{1} \\ $$
Commented by Olaf_Thorendsen last updated on 25/Jul/21

$$\mathrm{and}\:{n}\:=\:\mathrm{3} \\ $$
Commented by mathdanisur last updated on 25/Jul/21

$${Yes}\:{Ser},\:{but}\:{how} \\ $$
Commented by ajfour last updated on 25/Jul/21
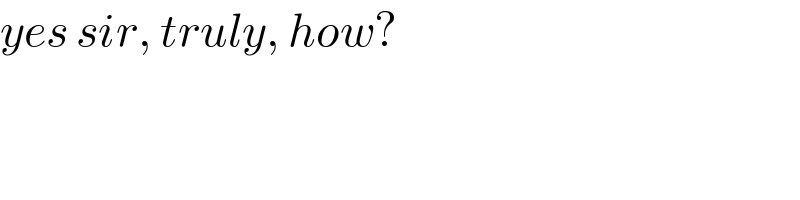
$${yes}\:{sir},\:{truly},\:{how}? \\ $$
Answered by mindispower last updated on 25/Jul/21
![Let n∈N suche Σ_(k=1) ^n k!=m^2 for n=1,n=3 we get solution ∀n≥4 Σ_(k=1) ^n k!=1+2!+3!+Σ_(k≥4) k!≡(1+2+6+24)[5] ≡3[5] n=5k,n^2 ≡0[5] n=(5k+_− 1)^2 ≡1[5] n=(5k+_− 2)≡4[5] so impossibl to get 3[5] ⇒∀n≥4; (√(Σ_(k=1) ^n k!))∉N n∈{1,3}](https://www.tinkutara.com/question/Q148178.png)
$${Let}\:{n}\in\mathbb{N}\:{suche} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}!={m}^{\mathrm{2}} \\ $$$${for}\:{n}=\mathrm{1},{n}=\mathrm{3}\:{we}\:{get}\:{solution} \\ $$$$\forall{n}\geqslant\mathrm{4} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}!=\mathrm{1}+\mathrm{2}!+\mathrm{3}!+\underset{{k}\geqslant\mathrm{4}} {\sum}{k}!\equiv\left(\mathrm{1}+\mathrm{2}+\mathrm{6}+\mathrm{24}\right)\left[\mathrm{5}\right] \\ $$$$\equiv\mathrm{3}\left[\mathrm{5}\right] \\ $$$${n}=\mathrm{5}{k},{n}^{\mathrm{2}} \equiv\mathrm{0}\left[\mathrm{5}\right] \\ $$$${n}=\left(\mathrm{5}{k}\underset{−} {+}\mathrm{1}\right)^{\mathrm{2}} \equiv\mathrm{1}\left[\mathrm{5}\right] \\ $$$${n}=\left(\mathrm{5}{k}\underset{−} {+}\mathrm{2}\right)\equiv\mathrm{4}\left[\mathrm{5}\right] \\ $$$${so}\:{impossibl}\:{to}\:{get}\:\mathrm{3}\left[\mathrm{5}\right] \\ $$$$\Rightarrow\forall{n}\geqslant\mathrm{4};\:\sqrt{\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}!}\notin\mathbb{N} \\ $$$${n}\in\left\{\mathrm{1},\mathrm{3}\right\} \\ $$
Commented by mathdanisur last updated on 26/Jul/21
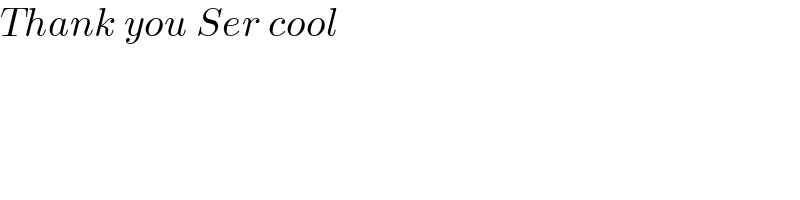
$${Thank}\:{you}\:{Ser}\:{cool} \\ $$
