Question Number 122108 by bemath last updated on 14/Nov/20
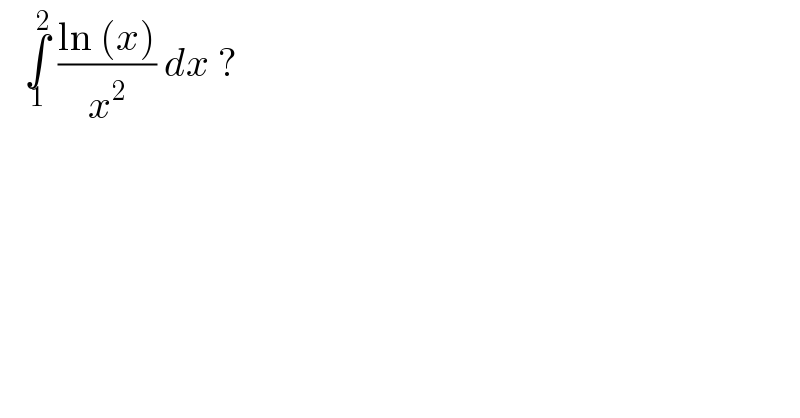
$$\:\:\:\underset{\mathrm{1}} {\overset{\mathrm{2}} {\int}}\:\frac{\mathrm{ln}\:\left({x}\right)}{{x}^{\mathrm{2}} }\:{dx}\:? \\ $$
Answered by Dwaipayan Shikari last updated on 14/Nov/20
![−[log(x)(1/x)]_1 ^2 +∫_1 ^2 (1/x^2 )dx =−((log2)/2)−((1/2)−1)=(1/2)(1−log(2))](https://www.tinkutara.com/question/Q122110.png)
$$−\left[{log}\left({x}\right)\frac{\mathrm{1}}{{x}}\right]_{\mathrm{1}} ^{\mathrm{2}} +\int_{\mathrm{1}} ^{\mathrm{2}} \frac{\mathrm{1}}{{x}^{\mathrm{2}} }{dx} \\ $$$$=−\frac{{log}\mathrm{2}}{\mathrm{2}}−\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−{log}\left(\mathrm{2}\right)\right) \\ $$
