Question Number 101793 by Dwaipayan Shikari last updated on 04/Jul/20
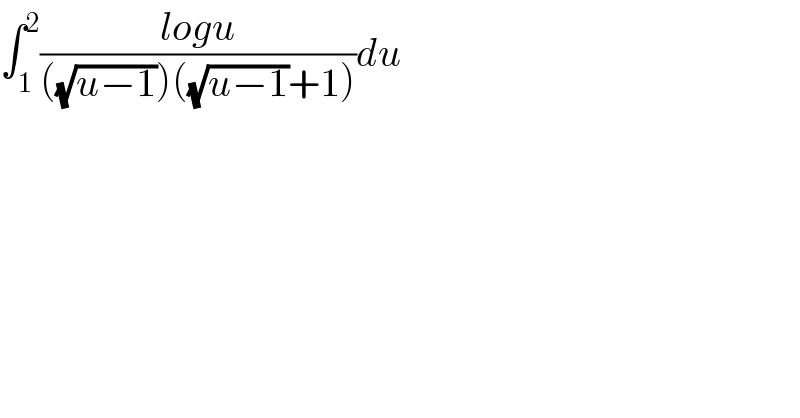
$$\int_{\mathrm{1}} ^{\mathrm{2}} \frac{{logu}}{\left(\sqrt{{u}−\mathrm{1}}\right)\left(\sqrt{{u}−\mathrm{1}}+\mathrm{1}\right)}{du} \\ $$
Answered by mathmax by abdo last updated on 05/Jul/20
![I =∫_1 ^(2 ) ((ln(u))/( (√(u−1))((√(u−1))+1)))du changement (√(u−1))=x give u−1 =x^2 ⇒ I =∫_0 ^1 ((ln(1+x^2 ))/(x(x+1))) (2x)dx =2 ∫_0 ^1 ((ln(1+x^2 ))/(1+x)) dx =2 ∫_0 ^1 ln(1+x^2 )Σ_(n=0) ^∞ (−1)^n x^n =2 Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 x^n ln(1+x^2 )dx =2 Σ_(n=0) ^∞ (−1)^n A_n with A_n =∫_0 ^1 x^n ln(1+x^2 )dx by parts we get A_n =[(x^(n+1) /(n+1))ln(1+x^2 )]_0 ^1 −∫_0 ^1 (x^(n+1) /(n+1))×((2x)/(1+x^2 ))dx =((ln(2))/(n+1))−(2/(n+1))∫_0 ^1 (x^(n+2) /(1+x^2 ))dx ∫_0 ^1 (x^(n+2) /(1+x^2 ))dx =∫_0 ^1 (((x^2 +1−1)x^n )/(1+x^2 ))dx =∫_0 ^1 x^n dx−∫_0 ^1 (x^n /(x^2 +1))dx =(1/(n+1))−∫_0 ^(1 ) (x^n /(x^2 +1))dx we have ∫_0 ^1 (x^n /(x^2 +1))dx =∫_0 ^1 x^n (Σ_(k=0) ^∞ (−1)^k x^(2k) ) =Σ_(k=0) ^∞ (−1)^k ∫_0 ^1 x^(n+2k) dx =Σ_(k=0) ^∞ (−1)^k ×(1/(n+2k+1)) ⇒ A_n =((ln2)/(n+1))−(2/(n+1)){(1/(n+1))−Σ_(k=0) ^∞ (((−1)^k )/(2k+n+1))} =((ln2)/(n+1))−(2/((n+1)^2 )) −(2/(n+1)) Σ_(k=0) ^∞ (((−1)^k )/(2k+n+1)) ⇒ I =2ln2 Σ_(n=0) ^∞ (((−1)^n )/(n+1))−4 Σ_(n=0) ^∞ (((−1)^n )/((n+1)^2 )) −4 Σ_(n=0) ^∞ (((−1)^n )/(n+1))(Σ_(k=0) ^∞ (((−1)^k )/(2k+n+1))) Σ_(n=0) ^∞ (((−1)^n )/(n+1)) =Σ_(n=1) ^∞ (((−1)^(n−1) )/n) =ln(2) Σ_(n=0) ^∞ (((−1)^n )/((n+1)^2 )) =Σ_(n=1) ^∞ (((−1)^(n−1) )/n^2 ) =−Σ_(n=1) ^∞ (((−1)^n )/n^2 ) =−{2^(1−2) −1)ξ(2) =−(−(1/2))×(π^2 /6) =(π^2 /(12)) Σ_(n=0) ^∞ (((−1)^n )/(n+1))Σ_(k=0) ^∞ (((−1)^k )/(2k+n+1)) =Σ_(n=0) ^∞ Σ_(k=0) ^∞ (((−1)^(n+k) )/((n+1)(2k+n+1))) ...be continued...](https://www.tinkutara.com/question/Q101829.png)
$$\mathrm{I}\:=\int_{\mathrm{1}} ^{\mathrm{2}\:} \:\frac{\mathrm{ln}\left(\mathrm{u}\right)}{\:\sqrt{\mathrm{u}−\mathrm{1}}\left(\sqrt{\mathrm{u}−\mathrm{1}}+\mathrm{1}\right)}\mathrm{du}\:\:\mathrm{changement}\:\sqrt{\mathrm{u}−\mathrm{1}}=\mathrm{x}\:\mathrm{give}\:\mathrm{u}−\mathrm{1}\:=\mathrm{x}^{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{x}\left(\mathrm{x}+\mathrm{1}\right)}\:\left(\mathrm{2x}\right)\mathrm{dx}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{1}+\mathrm{x}}\:\mathrm{dx} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{n}} \:=\mathrm{2}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{n}} \:\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\mathrm{dx} \\ $$$$=\mathrm{2}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{A}_{\mathrm{n}} \:\:\mathrm{with}\:\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{n}} \mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\mathrm{dx}\:\:\mathrm{by}\:\mathrm{parts}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{A}_{\mathrm{n}} =\left[\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}×\frac{\mathrm{2x}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\frac{\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{n}+\mathrm{1}}−\frac{\mathrm{2}}{\mathrm{n}+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{x}^{\mathrm{n}+\mathrm{2}} }{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\: \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{n}+\mathrm{2}} }{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}−\mathrm{1}\right)\mathrm{x}^{\mathrm{n}} }{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{n}} \:\mathrm{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}−\int_{\mathrm{0}} ^{\mathrm{1}\:} \:\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx}\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{n}} \left(\sum_{\mathrm{k}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{x}^{\mathrm{2k}} \right) \\ $$$$=\sum_{\mathrm{k}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{k}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{n}+\mathrm{2k}} \:\mathrm{dx}\:=\sum_{\mathrm{k}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{k}} \:×\frac{\mathrm{1}}{\mathrm{n}+\mathrm{2k}+\mathrm{1}}\:\Rightarrow \\ $$$$\mathrm{A}_{\mathrm{n}} =\frac{\mathrm{ln2}}{\mathrm{n}+\mathrm{1}}−\frac{\mathrm{2}}{\mathrm{n}+\mathrm{1}}\left\{\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}−\sum_{\mathrm{k}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} }{\mathrm{2k}+\mathrm{n}+\mathrm{1}}\right\} \\ $$$$=\frac{\mathrm{ln2}}{\mathrm{n}+\mathrm{1}}−\frac{\mathrm{2}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }\:−\frac{\mathrm{2}}{\mathrm{n}+\mathrm{1}}\:\sum_{\mathrm{k}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} }{\mathrm{2k}+\mathrm{n}+\mathrm{1}}\:\Rightarrow \\ $$$$\mathrm{I}\:=\mathrm{2ln2}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}+\mathrm{1}}−\mathrm{4}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }\:−\mathrm{4}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}+\mathrm{1}}\left(\sum_{\mathrm{k}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} }{\mathrm{2k}+\mathrm{n}+\mathrm{1}}\right) \\ $$$$\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}+\mathrm{1}}\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\:=\mathrm{ln}\left(\mathrm{2}\right) \\ $$$$\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}^{\mathrm{2}} }\:=−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}^{\mathrm{2}} }\:=−\left\{\mathrm{2}^{\mathrm{1}−\mathrm{2}} −\mathrm{1}\right)\xi\left(\mathrm{2}\right) \\ $$$$=−\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)×\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$$$\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}+\mathrm{1}}\sum_{\mathrm{k}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} }{\mathrm{2k}+\mathrm{n}+\mathrm{1}}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\sum_{\mathrm{k}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}+\mathrm{k}} }{\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{2k}+\mathrm{n}+\mathrm{1}\right)} \\ $$$$…\mathrm{be}\:\mathrm{continued}… \\ $$
Commented by 1549442205 last updated on 06/Jul/20
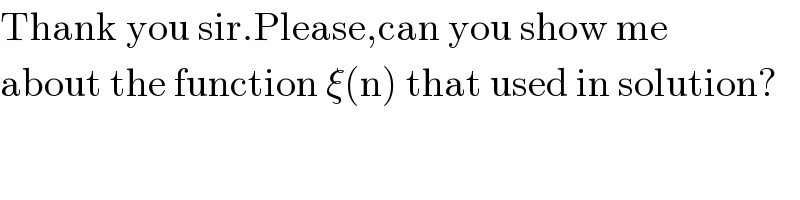
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}.\mathrm{Please},\mathrm{can}\:\mathrm{you}\:\mathrm{show}\:\mathrm{me} \\ $$$$\mathrm{about}\:\mathrm{the}\:\mathrm{function}\:\xi\left(\mathrm{n}\right)\:\mathrm{that}\:\mathrm{used}\:\mathrm{in}\:\mathrm{solution}? \\ $$
