Question Number 55360 by rahul 19 last updated on 22/Feb/19
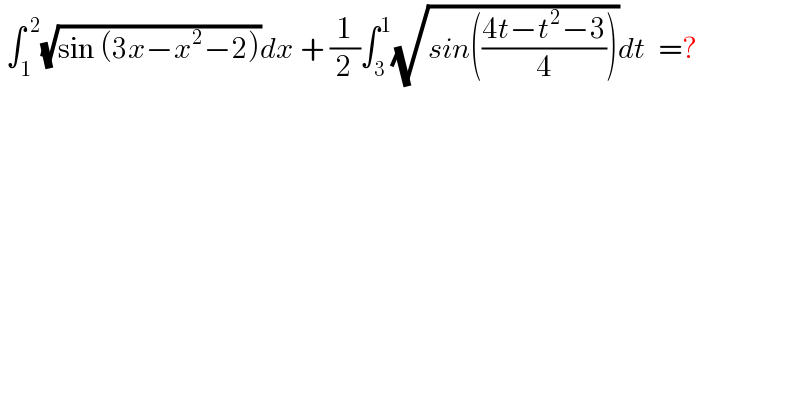
$$\:\int_{\mathrm{1}} ^{\:\mathrm{2}} \sqrt{\mathrm{sin}\:\left(\mathrm{3}{x}−{x}^{\mathrm{2}} −\mathrm{2}\right)}{dx}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{3}} ^{\mathrm{1}} \sqrt{{sin}\left(\frac{\mathrm{4}{t}−{t}^{\mathrm{2}} −\mathrm{3}}{\mathrm{4}}\right)}{dt}\:\:=? \\ $$
Commented by rahul 19 last updated on 22/Feb/19

$${Ans}:\:\mathrm{0}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 23/Feb/19
![−x^2 +3x−2→p(x) −x^2 +x+2x−2 −x(x−1)+2(x−1) (x−1)(2−x) p(x)=0 at x=1 and x=2 p(x)=+ve when 2>x>1 so (√(sinp(x))) making a loop with x axis ((4t−t^2 −3)/4)→q(t) ((−t^2 +t+3t−3)/4) ((−t(t−1)+3(t−1))/4) (((t−1)(3−t))/4) q(t)=0 when t=1and t=3 q(t)=+ve when 3>t>1 so sin((√((q(t))/4)) ) make a loop ∫_b ^a f(t)dt=∫_a ^b f(x)dx (1/2)∫_3 ^1 (√(sinq(t))) dt=(1/2)∫_3 ^1 (√(sinq(x))) dx now ∫_1 ^2 (√(sinp(x))) dx+(1/2)∫_3 ^1 (√(sinq(x))) dx =∫_1 ^2 (√(sinp(x))) dx−(1/2)∫_1 ^3 (√(sinq(x))) dx =[∫_1 ^2 (√(sknp(x))) −(1/2)(√(sinq(x))) dx]−(1/2)∫_2 ^3 (√(sinq(x))) dx wait...](https://www.tinkutara.com/question/Q55389.png)
$$−{x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{2}\rightarrow{p}\left({x}\right) \\ $$$$−{x}^{\mathrm{2}} +{x}+\mathrm{2}{x}−\mathrm{2} \\ $$$$−{x}\left({x}−\mathrm{1}\right)+\mathrm{2}\left({x}−\mathrm{1}\right) \\ $$$$\left({x}−\mathrm{1}\right)\left(\mathrm{2}−{x}\right) \\ $$$${p}\left({x}\right)=\mathrm{0}\:{at}\:{x}=\mathrm{1}\:{and}\:{x}=\mathrm{2} \\ $$$${p}\left({x}\right)=+{ve}\:\:\:{when}\:\mathrm{2}>{x}>\mathrm{1} \\ $$$${so}\:\sqrt{{sinp}\left({x}\right)}\:{making}\:{a}\:{loop}\:{with}\:{x}\:{axis} \\ $$$$\frac{\mathrm{4}{t}−{t}^{\mathrm{2}} −\mathrm{3}}{\mathrm{4}}\rightarrow{q}\left({t}\right) \\ $$$$\frac{−{t}^{\mathrm{2}} +{t}+\mathrm{3}{t}−\mathrm{3}}{\mathrm{4}} \\ $$$$\frac{−{t}\left({t}−\mathrm{1}\right)+\mathrm{3}\left({t}−\mathrm{1}\right)}{\mathrm{4}} \\ $$$$\frac{\left({t}−\mathrm{1}\right)\left(\mathrm{3}−{t}\right)}{\mathrm{4}} \\ $$$${q}\left({t}\right)=\mathrm{0}\:\:{when}\:{t}=\mathrm{1}{and}\:{t}=\mathrm{3} \\ $$$${q}\left({t}\right)=+{ve}\:{when}\:\:\mathrm{3}>{t}>\mathrm{1} \\ $$$${so}\:{sin}\left(\sqrt{\frac{{q}\left({t}\right)}{\mathrm{4}}}\:\right)\:{make}\:{a}\:{loop}\: \\ $$$$\int_{{b}} ^{{a}} {f}\left({t}\right){dt}=\int_{{a}} ^{{b}} {f}\left({x}\right){dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{3}} ^{\mathrm{1}} \sqrt{{sinq}\left({t}\right)}\:{dt}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{3}} ^{\mathrm{1}} \sqrt{{sinq}\left({x}\right)}\:{dx} \\ $$$${now} \\ $$$$\int_{\mathrm{1}} ^{\mathrm{2}} \sqrt{{sinp}\left({x}\right)}\:{dx}+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{3}} ^{\mathrm{1}} \sqrt{{sinq}\left({x}\right)}\:{dx} \\ $$$$=\int_{\mathrm{1}} ^{\mathrm{2}} \sqrt{{sinp}\left({x}\right)}\:{dx}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\mathrm{3}} \sqrt{{sinq}\left({x}\right)}\:{dx} \\ $$$$=\left[\int_{\mathrm{1}} ^{\mathrm{2}} \sqrt{{sknp}\left({x}\right)}\:−\frac{\mathrm{1}}{\mathrm{2}}\sqrt{{sinq}\left({x}\right)}\:{dx}\right]−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{2}} ^{\mathrm{3}} \sqrt{{sinq}\left({x}\right)}\:{dx} \\ $$$${wait}… \\ $$$$ \\ $$$$ \\ $$
Answered by MJS last updated on 25/Feb/19
![∫_1 ^2 (√(sin (3x−x^2 −2)))dx=∫_1 ^2 (√(−sin ((x−1)(x−2))))dx= [t=x−(3/2) → dx=dt] =∫_(−1/2) ^(1/2) (√(−sin (t^2 −(1/4))))dt=2∫_0 ^(1/2) (√(−sin (t^2 −(1/4))))dt= [u=t^2 −(1/4) → dt=(du/(2t))] =2∫_(−1/4) ^0 (√(−((sin u)/(4u+1))))du=I_1 (1/2)∫_3 ^1 (√(sin (((4x−x^2 −3)/4))))dx=−(1/2)∫_1 ^3 (√(−sin (((x−1)(x−3))/4)))dx= [t=x−2 → dx=dt] =−(1/2)∫_(−1) ^1 (√(−sin ((t^2 −1)/4)))dt=−∫_0 ^1 (√(−sin ((t^2 −1)/4)))dt= [u=((t^2 −1)/4) → dt=((2du)/t)] =−2∫_(−1/4) ^0 (√(−((sin u)/(4u+1))))du=I_2 I_1 +I_2 =0](https://www.tinkutara.com/question/Q55481.png)
$$\underset{\mathrm{1}} {\overset{\mathrm{2}} {\int}}\sqrt{\mathrm{sin}\:\left(\mathrm{3}{x}−{x}^{\mathrm{2}} −\mathrm{2}\right)}{dx}=\underset{\mathrm{1}} {\overset{\mathrm{2}} {\int}}\sqrt{−\mathrm{sin}\:\left(\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)\right)}{dx}= \\ $$$$\:\:\:\:\:\left[{t}={x}−\frac{\mathrm{3}}{\mathrm{2}}\:\rightarrow\:{dx}={dt}\right] \\ $$$$=\underset{−\mathrm{1}/\mathrm{2}} {\overset{\mathrm{1}/\mathrm{2}} {\int}}\sqrt{−\mathrm{sin}\:\left({t}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}\right)}{dt}=\mathrm{2}\underset{\mathrm{0}} {\overset{\mathrm{1}/\mathrm{2}} {\int}}\sqrt{−\mathrm{sin}\:\left({t}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}\right)}{dt}= \\ $$$$\:\:\:\:\:\left[{u}={t}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}\:\rightarrow\:{dt}=\frac{{du}}{\mathrm{2}{t}}\right] \\ $$$$=\mathrm{2}\underset{−\mathrm{1}/\mathrm{4}} {\overset{\mathrm{0}} {\int}}\sqrt{−\frac{\mathrm{sin}\:{u}}{\mathrm{4}{u}+\mathrm{1}}}{du}={I}_{\mathrm{1}} \\ $$$$ \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{3}} {\overset{\mathrm{1}} {\int}}\sqrt{\mathrm{sin}\:\left(\frac{\mathrm{4}{x}−{x}^{\mathrm{2}} −\mathrm{3}}{\mathrm{4}}\right)}{dx}=−\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{1}} {\overset{\mathrm{3}} {\int}}\sqrt{−\mathrm{sin}\:\frac{\left({x}−\mathrm{1}\right)\left({x}−\mathrm{3}\right)}{\mathrm{4}}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}={x}−\mathrm{2}\:\rightarrow\:{dx}={dt}\right] \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\underset{−\mathrm{1}} {\overset{\mathrm{1}} {\int}}\sqrt{−\mathrm{sin}\:\frac{{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{4}}}{dt}=−\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\sqrt{−\mathrm{sin}\:\frac{{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{4}}}{dt}= \\ $$$$\:\:\:\:\:\left[{u}=\frac{{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{4}}\:\rightarrow\:{dt}=\frac{\mathrm{2}{du}}{{t}}\right] \\ $$$$=−\mathrm{2}\underset{−\mathrm{1}/\mathrm{4}} {\overset{\mathrm{0}} {\int}}\sqrt{−\frac{\mathrm{sin}\:{u}}{\mathrm{4}{u}+\mathrm{1}}}{du}={I}_{\mathrm{2}} \\ $$$$ \\ $$$${I}_{\mathrm{1}} +{I}_{\mathrm{2}} =\mathrm{0} \\ $$
Commented by rahul 19 last updated on 25/Feb/19

$${thank}\:{you}\:{Sir}! \\ $$
