Menu Close

1-2-x-gt-1-x-1-

Tinku Tara 0 Comments
Pin




Question Number 164568 by leonhard77 last updated on 19/Jan/22
(1/( (√(2−x)))) > (1/(x−1))
$$\:\:\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}−{x}}}\:>\:\frac{\mathrm{1}}{{x}−\mathrm{1}} \\ $$
Answered by TheSupreme last updated on 19/Jan/22
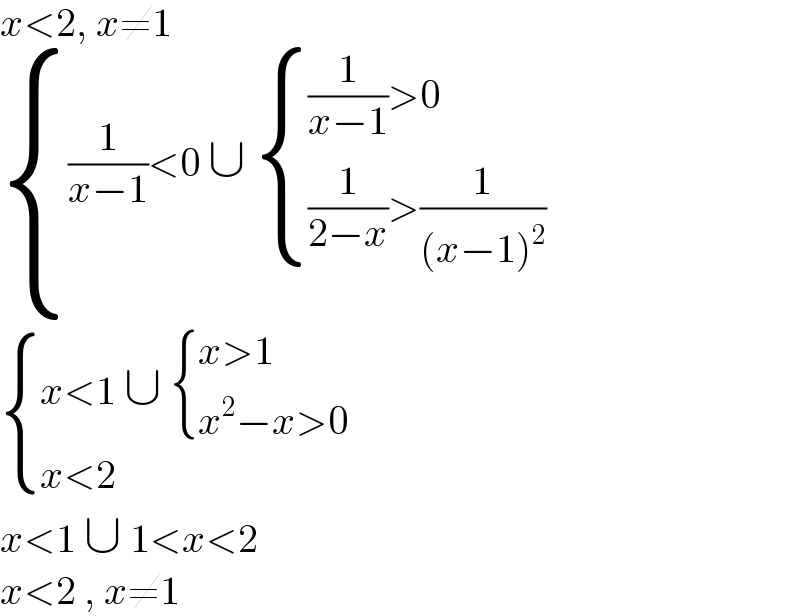
x<2, x≠1 { (((1/(x−1))<0 ∪ { (((1/(x−1))>0)),(((1/(2−x))>(1/((x−1)^2 )))) :})),() :} { ((x<1 ∪ { ((x>1)),((x^2 −x>0)) :})),((x<2 )) :} x<1 ∪ 1<x<2 x<2 , x≠1
$${x}<\mathrm{2},\:{x}\neq\mathrm{1} \\ $$$$\begin{cases}{\frac{\mathrm{1}}{{x}−\mathrm{1}}<\mathrm{0}\:\cup\:\begin{cases}{\frac{\mathrm{1}}{{x}−\mathrm{1}}>\mathrm{0}}\\{\frac{\mathrm{1}}{\mathrm{2}−{x}}>\frac{\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }}\end{cases}}\\{}\end{cases} \\ $$$$\begin{cases}{{x}<\mathrm{1}\:\cup\:\begin{cases}{{x}>\mathrm{1}}\\{{x}^{\mathrm{2}} −{x}>\mathrm{0}}\end{cases}}\\{{x}<\mathrm{2}\:}\end{cases} \\ $$$${x}<\mathrm{1}\:\cup\:\mathrm{1}<{x}<\mathrm{2} \\ $$$${x}<\mathrm{2}\:,\:{x}\neq\mathrm{1} \\ $$
Answered by alephzero last updated on 19/Jan/22
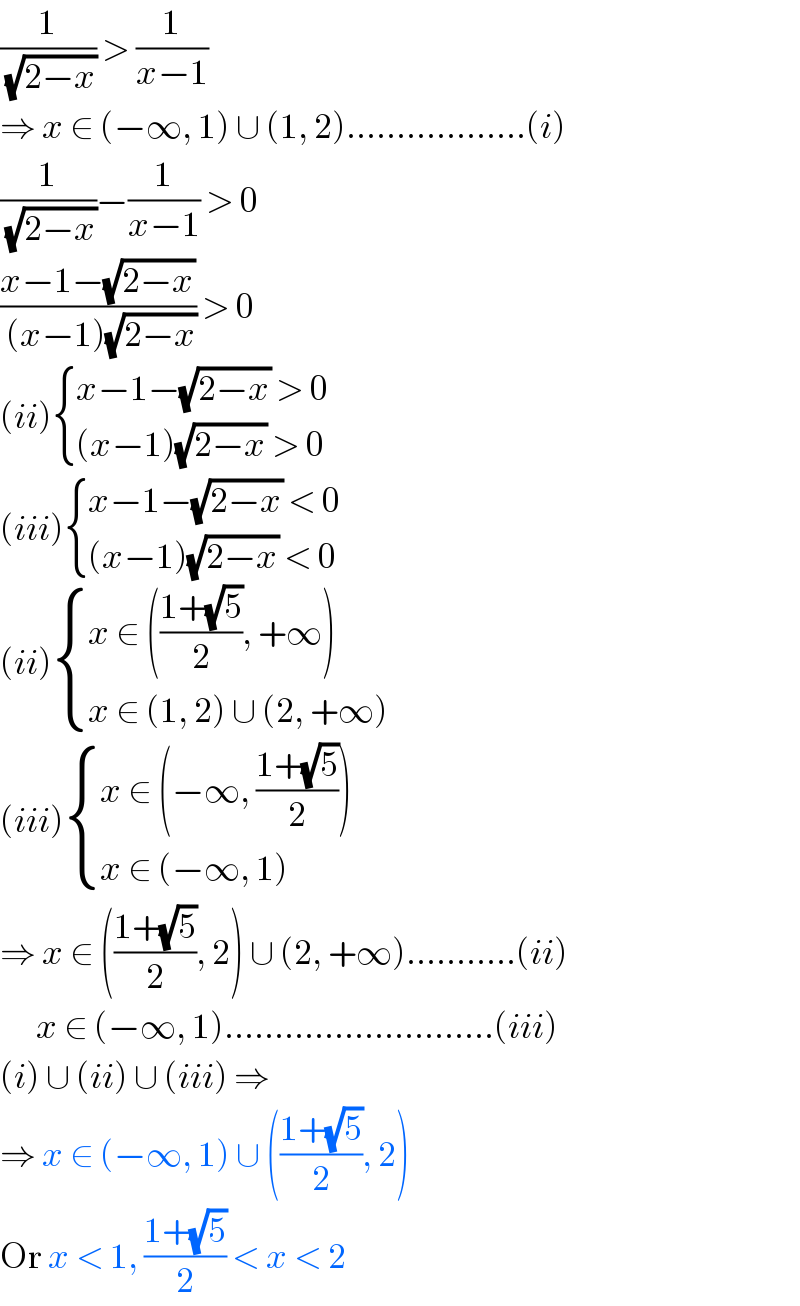
(1/( (√(2−x)))) > (1/(x−1)) ⇒ x ∈ (−∞, 1) ∪ (1, 2)..................(i) (1/( (√(2−x))))−(1/(x−1)) > 0 ((x−1−(√(2−x)))/( (x−1)(√(2−x)))) > 0 (ii) { ((x−1−(√(2−x)) > 0)),(((x−1)(√(2−x)) > 0)) :} (iii) { ((x−1−(√(2−x)) < 0)),(((x−1)(√(2−x)) < 0)) :} (ii) { ((x ∈ (((1+(√5))/2), +∞))),((x ∈ (1, 2) ∪ (2, +∞))) :} (iii) { ((x ∈ (−∞, ((1+(√5))/2)))),((x ∈ (−∞, 1))) :} ⇒ x ∈ (((1+(√5))/2), 2) ∪ (2, +∞)...........(ii) x ∈ (−∞, 1)...........................(iii) (i) ∪ (ii) ∪ (iii) ⇒ ⇒ x ∈ (−∞, 1) ∪ (((1+(√5))/2), 2) Or x < 1, ((1+(√5))/2) < x < 2
$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}−{x}}}\:>\:\frac{\mathrm{1}}{{x}−\mathrm{1}} \\ $$$$\Rightarrow\:{x}\:\in\:\left(−\infty,\:\mathrm{1}\right)\:\cup\:\left(\mathrm{1},\:\mathrm{2}\right)………………\left({i}\right) \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}−{x}}}−\frac{\mathrm{1}}{{x}−\mathrm{1}}\:>\:\mathrm{0} \\ $$$$\frac{{x}−\mathrm{1}−\sqrt{\mathrm{2}−{x}}}{\:\left({x}−\mathrm{1}\right)\sqrt{\mathrm{2}−{x}}}\:>\:\mathrm{0} \\ $$$$\left({ii}\right)\begin{cases}{{x}−\mathrm{1}−\sqrt{\mathrm{2}−{x}}\:>\:\mathrm{0}}\\{\left({x}−\mathrm{1}\right)\sqrt{\mathrm{2}−{x}}\:>\:\mathrm{0}}\end{cases} \\ $$$$\left({iii}\right)\begin{cases}{{x}−\mathrm{1}−\sqrt{\mathrm{2}−{x}}\:<\:\mathrm{0}}\\{\left({x}−\mathrm{1}\right)\sqrt{\mathrm{2}−{x}}\:<\:\mathrm{0}}\end{cases} \\ $$$$\left({ii}\right)\begin{cases}{{x}\:\in\:\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}},\:+\infty\right)}\\{{x}\:\in\:\left(\mathrm{1},\:\mathrm{2}\right)\:\cup\:\left(\mathrm{2},\:+\infty\right)}\end{cases} \\ $$$$\left({iii}\right)\begin{cases}{{x}\:\in\:\left(−\infty,\:\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)}\\{{x}\:\in\:\left(−\infty,\:\mathrm{1}\right)}\end{cases} \\ $$$$\Rightarrow\:{x}\:\in\:\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}},\:\mathrm{2}\right)\:\cup\:\left(\mathrm{2},\:+\infty\right)………..\left({ii}\right) \\ $$$$\:\:\:\:\:\:{x}\:\in\:\left(−\infty,\:\mathrm{1}\right)………………………\left({iii}\right) \\ $$$$\left({i}\right)\:\cup\:\left({ii}\right)\:\cup\:\left({iii}\right)\:\Rightarrow \\ $$$$\Rightarrow\:{x}\:\in\:\left(−\infty,\:\mathrm{1}\right)\:\cup\:\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}},\:\mathrm{2}\right) \\ $$$$\mathrm{Or}\:{x}\:<\:\mathrm{1},\:\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\:<\:{x}\:<\:\mathrm{2} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *