Question Number 57329 by naka3546 last updated on 02/Apr/19
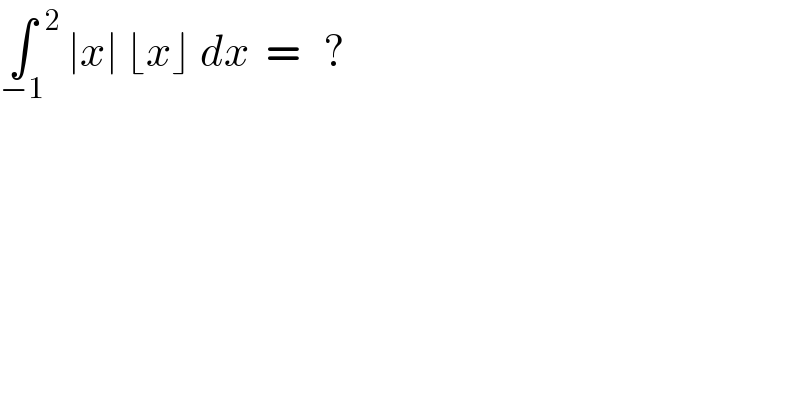
$$\underset{−\mathrm{1}} {\int}\overset{\mathrm{2}} {\:}\:\mid{x}\mid\:\lfloor{x}\rfloor\:{dx}\:\:=\:\:\:? \\ $$
Commented by turbo msup by abdo last updated on 02/Apr/19
![I=∫_(−1) ^0 ∣x∣[x]dx +∫_0 ^1 ∣x∣[x]dx/+∫_1 ^2 ∣x∣[x]dx =∫_(−1) ^0 −x(−1)dx +0 +∫_1 ^2 xdx =[(x^2 /2)]_(−1) ^0 +[(x^2 /2)]_1 ^2 =−(1/2) +2−(1/2) ⇒I=1 .](https://www.tinkutara.com/question/Q57334.png)
$${I}=\int_{−\mathrm{1}} ^{\mathrm{0}} \mid{x}\mid\left[{x}\right]{dx}\:+\int_{\mathrm{0}} ^{\mathrm{1}} \mid{x}\mid\left[{x}\right]{dx}/+\int_{\mathrm{1}} ^{\mathrm{2}} \mid{x}\mid\left[{x}\right]{dx} \\ $$$$=\int_{−\mathrm{1}} ^{\mathrm{0}} −{x}\left(−\mathrm{1}\right){dx}\:+\mathrm{0}\:+\int_{\mathrm{1}} ^{\mathrm{2}} {xdx} \\ $$$$=\left[\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right]_{−\mathrm{1}} ^{\mathrm{0}} \:+\left[\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{1}} ^{\mathrm{2}} \:=−\frac{\mathrm{1}}{\mathrm{2}}\:+\mathrm{2}−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{I}=\mathrm{1}\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 02/Apr/19
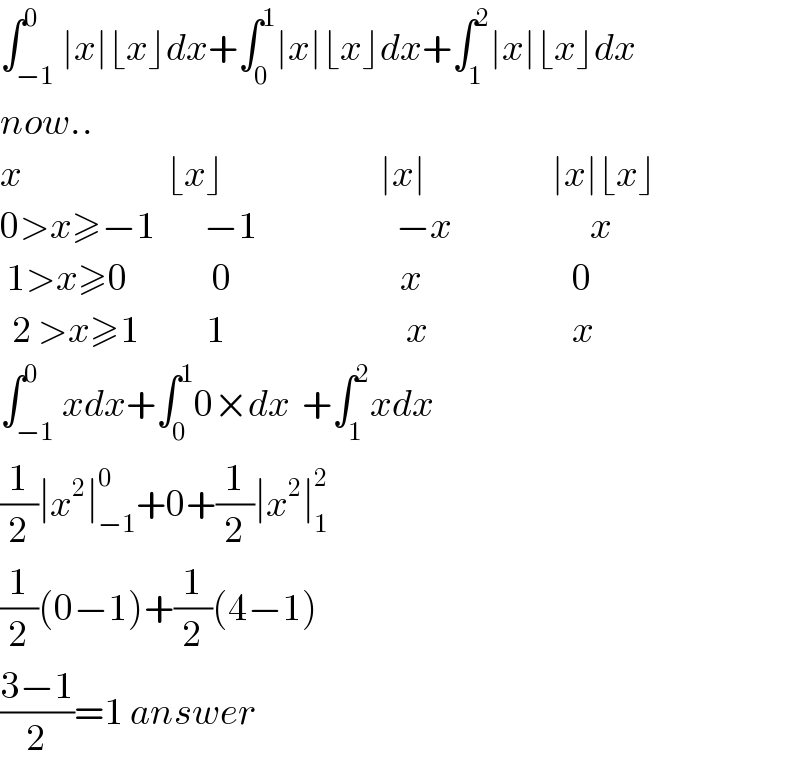
$$\int_{−\mathrm{1}} ^{\mathrm{0}} \mid{x}\mid\lfloor{x}\rfloor{dx}+\int_{\mathrm{0}} ^{\mathrm{1}} \mid{x}\mid\lfloor{x}\rfloor{dx}+\int_{\mathrm{1}} ^{\mathrm{2}} \mid{x}\mid\lfloor{x}\rfloor{dx} \\ $$$${now}.. \\ $$$${x}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\lfloor{x}\rfloor\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid{x}\mid\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid{x}\mid\lfloor{x}\rfloor \\ $$$$\mathrm{0}>{x}\geqslant−\mathrm{1}\:\:\:\:\:\:\:\:−\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−{x}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x} \\ $$$$\:\mathrm{1}>{x}\geqslant\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0} \\ $$$$\:\:\mathrm{2}\:>{x}\geqslant\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x} \\ $$$$\int_{−\mathrm{1}} ^{\mathrm{0}} {xdx}+\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{0}×{dx}\:\:+\int_{\mathrm{1}} ^{\mathrm{2}} {xdx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\mid{x}^{\mathrm{2}} \mid_{−\mathrm{1}} ^{\mathrm{0}} +\mathrm{0}+\frac{\mathrm{1}}{\mathrm{2}}\mid{x}^{\mathrm{2}} \mid_{\mathrm{1}} ^{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{0}−\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{4}−\mathrm{1}\right) \\ $$$$\frac{\mathrm{3}−\mathrm{1}}{\mathrm{2}}=\mathrm{1}\:{answer} \\ $$
