Question Number 157546 by naka3546 last updated on 24/Oct/21

$$\left(\underset{\mathrm{1}} {\overset{\mathrm{2002}} {\:}}\right)\:+\:\left(\underset{\mathrm{4}} {\overset{\mathrm{2002}} {\:}}\right)\:+\:\left(\underset{\mathrm{7}} {\overset{\mathrm{2002}} {\:}}\right)\:+\:\ldots+\:\left(\underset{\mathrm{2002}} {\overset{\mathrm{2002}} {\:}}\right)\:\:=\:? \\ $$$${Thank}\:\:{you}\:\:{so}\:\:{much}\:. \\ $$
Commented by mr W last updated on 24/Oct/21

$${please}\:{check}\:{the}\:{question}! \\ $$$${something}\:{is}\:{not}\:{proper}: \\ $$$$\mathrm{1},\mathrm{4},\mathrm{7},\mathrm{10},…,\mathrm{1999},\mathrm{2002} \\ $$$${so}\:{term}\:\begin{pmatrix}{\mathrm{2003}}\\{\mathrm{2003}}\end{pmatrix}\:{doesn}'{t}\:{match}. \\ $$
Commented by naka3546 last updated on 24/Oct/21

$${yes},\:{sir}.\:\:{But}\:\:{the}\:\:{question}\:\:{like}\:\:{that}\:. \\ $$$${What}\:\:{method}\:\:{should}\:\:{I}\:\:{use}\:\:{for}\:\:{solving}\:\:{it}\:. \\ $$$${Any}\:\:{method}\:\:{to}\:\:{solve}\:\:{it}\:\:{if}\:\:{the}\:\:{term}\:\:{doesn}'{t}\:\:{match}\:\:? \\ $$
Commented by naka3546 last updated on 24/Oct/21

$${I}\:'{ve}\:\:{changed}\:\:{the}\:\:{question}\:\:{just}\:\:{now}\:,\:{sir}. \\ $$
Commented by mr W last updated on 24/Oct/21

$${i}\:{got} \\ $$$$\left(\underset{\mathrm{1}} {\overset{\mathrm{2002}} {\:}}\right)\:+\:\left(\underset{\mathrm{4}} {\overset{\mathrm{2002}} {\:}}\right)\:+\:\left(\underset{\mathrm{7}} {\overset{\mathrm{2002}} {\:}}\right)\:+\:\ldots+\:\left(\underset{\mathrm{2002}} {\overset{\mathrm{2002}} {\:}}\right)\:\:=\:\frac{\mathrm{2}^{\mathrm{2002}} −\mathrm{1}}{\mathrm{3}} \\ $$$${right}? \\ $$
Commented by mr W last updated on 24/Oct/21
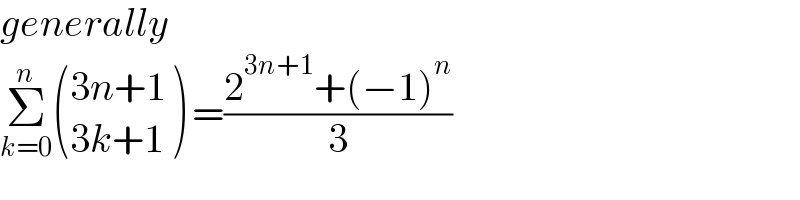
$${generally} \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{\mathrm{3}{n}+\mathrm{1}}\\{\mathrm{3}{k}+\mathrm{1}}\end{pmatrix}\:=\frac{\mathrm{2}^{\mathrm{3}{n}+\mathrm{1}} +\left(−\mathrm{1}\right)^{{n}} }{\mathrm{3}} \\ $$
Answered by mr W last updated on 24/Oct/21
![find Σ_(k=0) ^n (((3n+1)),((3k+1)) ) =? (1+x)^(3n+1) =Σ_(r=0) ^(3n+1) (((3n+1)),(r) ) x^r (1+x)^(3n+1) =Σ_(k=0) ^n (((3n+1)),((3k)) ) x^(3k) +Σ_(k=0) ^n (((3n+1)),((3k+1)) ) x^(3k+1) +Σ_(k=0) ^(n−1) (((3n+1)),((3k+2)) ) x^(3k+2) let x=1 (1+1)^(3n+1) =Σ_(k=0) ^n (((3n+1)),((3k)) ) _(−A −) +Σ_(k=0) ^n (((3n+1)),((3k+1)) ) _(−B −) +Σ_(k=0) ^(n−1) (((3n+1)),((3k+2)) ) _(− C −) ⇒ 2^(3n+1) =A +B+C ...(I) let x=ω (1+ω)^(3n+1) =Σ_(k=0) ^n (((3n+1)),((3k)) ) +ωΣ_(k=0) ^n (((3n+1)),((3k+1)) ) +ω^2 Σ_(k=0) ^(n−1) (((3n+1)),((3k+2)) ) ⇒ (1+ω)^(3n+1) =A+ωB+ω^2 C ...(II) let x=ω^2 (1+ω^2 )^(3n+1) =Σ_(k=0) ^n (((3n+1)),((3k)) ) +ω^2 Σ_(k=0) ^n (((3n+1)),((3k+1)) ) +ωΣ_(k=0) ^(n−1) (((3n+1)),((3k+2)) ) ⇒(1+ω^2 )^(3n+1) =A+ω^2 B+ωC ...(III) (II)−(I): (ω−1)B+(ω^2 −1)C=(1+ω)^(3n+1) −2^(3n+1) (ω−1)B+(ω^2 −1)C=−(−1)^n ω^2 −2^(3n+1) ...(IV) (III)−(I): (ω^2 −1)B+(ω−1)C=−(−1)^n ω−2^(3n+1) (ω^2 −1)(ω+1)B+(ω^2 −1)C=−(−1)^n ω(ω+1)−2^(3n+1) (ω+1) ...(V) (V)−(IV): (ω−1)[(ω+1)^2 −1]B=−(−1)^n ω−2^(3n+1) ω (ω−1)(ω+2)B=−(−1)^n −2^(3n+1) (−3)B=−(−1)^n −2^(3n+1) ⇒B=(((−1)^n +2^(3n+1) )/3) i.e. Σ_(k=0) ^n (((3n+1)),((3k+1)) ) =((2^(3n+1) +(−1)^n )/3) with n=667 ⇒Σ_(k=0) ^(667) (((2002)),((3k+1)) ) =((2^(2002) −1)/3)](https://www.tinkutara.com/question/Q157579.png)
$${find}\:\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{\mathrm{3}{n}+\mathrm{1}}\\{\mathrm{3}{k}+\mathrm{1}}\end{pmatrix}\:=? \\ $$$$ \\ $$$$\left(\mathrm{1}+{x}\right)^{\mathrm{3}{n}+\mathrm{1}} =\underset{{r}=\mathrm{0}} {\overset{\mathrm{3}{n}+\mathrm{1}} {\sum}}\begin{pmatrix}{\mathrm{3}{n}+\mathrm{1}}\\{{r}}\end{pmatrix}\:{x}^{{r}} \\ $$$$\left(\mathrm{1}+{x}\right)^{\mathrm{3}{n}+\mathrm{1}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{\mathrm{3}{n}+\mathrm{1}}\\{\mathrm{3}{k}}\end{pmatrix}\:{x}^{\mathrm{3}{k}} +\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{\mathrm{3}{n}+\mathrm{1}}\\{\mathrm{3}{k}+\mathrm{1}}\end{pmatrix}\:{x}^{\mathrm{3}{k}+\mathrm{1}} +\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\begin{pmatrix}{\mathrm{3}{n}+\mathrm{1}}\\{\mathrm{3}{k}+\mathrm{2}}\end{pmatrix}\:{x}^{\mathrm{3}{k}+\mathrm{2}} \\ $$$${let}\:{x}=\mathrm{1} \\ $$$$\left(\mathrm{1}+\mathrm{1}\right)^{\mathrm{3}{n}+\mathrm{1}} =\underset{−{A}\:−} {\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{\mathrm{3}{n}+\mathrm{1}}\\{\mathrm{3}{k}}\end{pmatrix}\:}+\underset{−{B}\:−} {\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{\mathrm{3}{n}+\mathrm{1}}\\{\mathrm{3}{k}+\mathrm{1}}\end{pmatrix}\:}+\underset{−\:{C}\:−} {\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\begin{pmatrix}{\mathrm{3}{n}+\mathrm{1}}\\{\mathrm{3}{k}+\mathrm{2}}\end{pmatrix}\:} \\ $$$$\Rightarrow\:\mathrm{2}^{\mathrm{3}{n}+\mathrm{1}} ={A}\:+{B}+{C}\:\:\:…\left({I}\right) \\ $$$${let}\:{x}=\omega \\ $$$$\left(\mathrm{1}+\omega\right)^{\mathrm{3}{n}+\mathrm{1}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{\mathrm{3}{n}+\mathrm{1}}\\{\mathrm{3}{k}}\end{pmatrix}\:+\omega\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{\mathrm{3}{n}+\mathrm{1}}\\{\mathrm{3}{k}+\mathrm{1}}\end{pmatrix}\:+\omega^{\mathrm{2}} \underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\begin{pmatrix}{\mathrm{3}{n}+\mathrm{1}}\\{\mathrm{3}{k}+\mathrm{2}}\end{pmatrix}\: \\ $$$$\Rightarrow\:\left(\mathrm{1}+\omega\right)^{\mathrm{3}{n}+\mathrm{1}} ={A}+\omega{B}+\omega^{\mathrm{2}} {C}\:\:\:…\left({II}\right) \\ $$$${let}\:{x}=\omega^{\mathrm{2}} \\ $$$$\left(\mathrm{1}+\omega^{\mathrm{2}} \right)^{\mathrm{3}{n}+\mathrm{1}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{\mathrm{3}{n}+\mathrm{1}}\\{\mathrm{3}{k}}\end{pmatrix}\:+\omega^{\mathrm{2}} \underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{\mathrm{3}{n}+\mathrm{1}}\\{\mathrm{3}{k}+\mathrm{1}}\end{pmatrix}\:+\omega\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\begin{pmatrix}{\mathrm{3}{n}+\mathrm{1}}\\{\mathrm{3}{k}+\mathrm{2}}\end{pmatrix}\: \\ $$$$\Rightarrow\left(\mathrm{1}+\omega^{\mathrm{2}} \right)^{\mathrm{3}{n}+\mathrm{1}} ={A}+\omega^{\mathrm{2}} {B}+\omega{C}\:\:\:\:…\left({III}\right) \\ $$$$ \\ $$$$\left({II}\right)−\left({I}\right): \\ $$$$\left(\omega−\mathrm{1}\right){B}+\left(\omega^{\mathrm{2}} −\mathrm{1}\right){C}=\left(\mathrm{1}+\omega\right)^{\mathrm{3}{n}+\mathrm{1}} −\mathrm{2}^{\mathrm{3}{n}+\mathrm{1}} \\ $$$$\left(\omega−\mathrm{1}\right){B}+\left(\omega^{\mathrm{2}} −\mathrm{1}\right){C}=−\left(−\mathrm{1}\right)^{{n}} \omega^{\mathrm{2}} −\mathrm{2}^{\mathrm{3}{n}+\mathrm{1}} \:\:\:…\left({IV}\right) \\ $$$$\left({III}\right)−\left({I}\right): \\ $$$$\left(\omega^{\mathrm{2}} −\mathrm{1}\right){B}+\left(\omega−\mathrm{1}\right){C}=−\left(−\mathrm{1}\right)^{{n}} \omega−\mathrm{2}^{\mathrm{3}{n}+\mathrm{1}} \\ $$$$\left(\omega^{\mathrm{2}} −\mathrm{1}\right)\left(\omega+\mathrm{1}\right){B}+\left(\omega^{\mathrm{2}} −\mathrm{1}\right){C}=−\left(−\mathrm{1}\right)^{{n}} \omega\left(\omega+\mathrm{1}\right)−\mathrm{2}^{\mathrm{3}{n}+\mathrm{1}} \left(\omega+\mathrm{1}\right)\:\:\:…\left({V}\right) \\ $$$$\left({V}\right)−\left({IV}\right): \\ $$$$\left(\omega−\mathrm{1}\right)\left[\left(\omega+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}\right]{B}=−\left(−\mathrm{1}\right)^{{n}} \omega−\mathrm{2}^{\mathrm{3}{n}+\mathrm{1}} \omega \\ $$$$\left(\omega−\mathrm{1}\right)\left(\omega+\mathrm{2}\right){B}=−\left(−\mathrm{1}\right)^{{n}} −\mathrm{2}^{\mathrm{3}{n}+\mathrm{1}} \\ $$$$\left(−\mathrm{3}\right){B}=−\left(−\mathrm{1}\right)^{{n}} −\mathrm{2}^{\mathrm{3}{n}+\mathrm{1}} \\ $$$$\Rightarrow{B}=\frac{\left(−\mathrm{1}\right)^{{n}} +\mathrm{2}^{\mathrm{3}{n}+\mathrm{1}} }{\mathrm{3}} \\ $$$${i}.{e}.\:\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{\mathrm{3}{n}+\mathrm{1}}\\{\mathrm{3}{k}+\mathrm{1}}\end{pmatrix}\:=\frac{\mathrm{2}^{\mathrm{3}{n}+\mathrm{1}} +\left(−\mathrm{1}\right)^{{n}} }{\mathrm{3}} \\ $$$${with}\:{n}=\mathrm{667} \\ $$$$\Rightarrow\underset{{k}=\mathrm{0}} {\overset{\mathrm{667}} {\sum}}\begin{pmatrix}{\mathrm{2002}}\\{\mathrm{3}{k}+\mathrm{1}}\end{pmatrix}\:=\frac{\mathrm{2}^{\mathrm{2002}} −\mathrm{1}}{\mathrm{3}} \\ $$
Commented by Tawa11 last updated on 25/Oct/21

$$\mathrm{Great} \\ $$
