Menu Close

1-2014-2-2014-3-2014-1007-2014-

Tinku Tara 0 Comments
Pin




Question Number 162035 by naka3546 last updated on 25/Dec/21
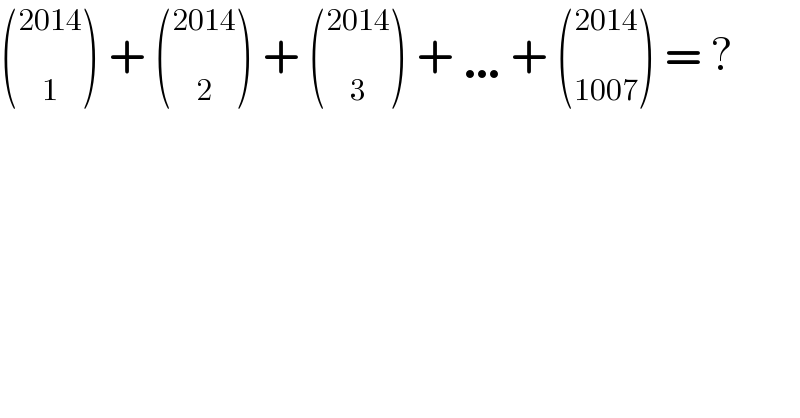
( _1 ^(2014) ) + ( _2 ^(2014) ) + ( _3 ^(2014) ) + …+ ( _(1007) ^(2014) ) = ?
$$\left(\underset{\mathrm{1}} {\overset{\mathrm{2014}} {\:}}\right)\:+\:\left(\underset{\mathrm{2}} {\overset{\mathrm{2014}} {\:}}\right)\:+\:\left(\underset{\mathrm{3}} {\overset{\mathrm{2014}} {\:}}\right)\:+\:\ldots+\:\left(\underset{\mathrm{1007}} {\overset{\mathrm{2014}} {\:}}\right)\:=\:? \\ $$
Answered by Rasheed.Sindhi last updated on 26/Dec/21
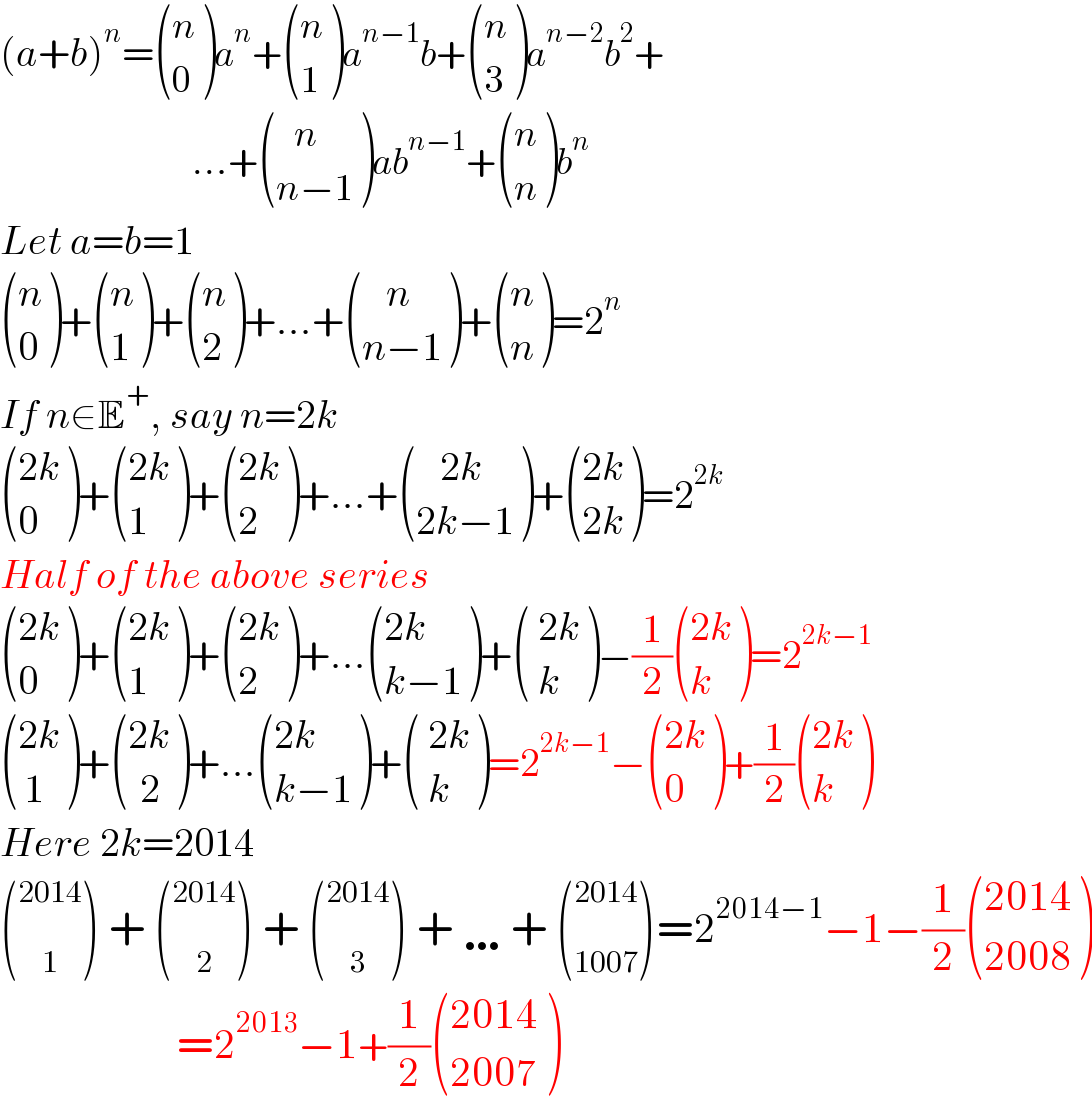
(a+b)^n = ((n),(0) )a^n + ((n),(1) )a^(n−1) b+ ((n),(3) )a^(n−2) b^2 + ...+ ((( n)),((n−1)) )ab^(n−1) + ((n),(n) )b^n Let a=b=1 ((n),(0) )+ ((n),(1) )+ ((n),(2) )+...+ ((( n)),((n−1)) )+ ((n),(n) )=2^n If n∈E^+ , say n=2k (((2k)),(0) )+ (((2k)),(1) )+ (((2k)),(2) )+...+ ((( 2k)),((2k−1)) )+ (((2k)),((2k)) )=2^(2k) Half of the above series (((2k)),(0) )+ (((2k)),(1) )+ (((2k)),(2) )+... (((2k)),((k−1)) )+ ((( 2k)),(( k)) )−(1/2) (((2k)),(k) )=2^(2k−1) (((2k)),(( 1)) )+ (((2k)),(( 2)) )+... (((2k)),((k−1)) )+ ((( 2k)),(( k)) )=2^(2k−1) − (((2k)),(0) )+(1/2) (((2k)),(k) ) Here 2k=2014 ( _1 ^(2014) ) + ( _2 ^(2014) ) + ( _3 ^(2014) ) + …+ ( _(1007) ^(2014) )=2^(2014−1) −1−(1/2) (((2014)),((2008)) ) =2^(2013) −1+(1/2) (((2014)),((2007)) )
$$\left({a}+{b}\right)^{{n}} =\begin{pmatrix}{{n}}\\{\mathrm{0}}\end{pmatrix}{a}^{{n}} +\begin{pmatrix}{{n}}\\{\mathrm{1}}\end{pmatrix}{a}^{{n}−\mathrm{1}} {b}+\begin{pmatrix}{{n}}\\{\mathrm{3}}\end{pmatrix}{a}^{{n}−\mathrm{2}} {b}^{\mathrm{2}} + \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…+\begin{pmatrix}{\:\:\:{n}}\\{{n}−\mathrm{1}}\end{pmatrix}{ab}^{{n}−\mathrm{1}} +\begin{pmatrix}{{n}}\\{{n}}\end{pmatrix}{b}^{{n}} \\ $$$${Let}\:{a}={b}=\mathrm{1} \\ $$$$\begin{pmatrix}{{n}}\\{\mathrm{0}}\end{pmatrix}+\begin{pmatrix}{{n}}\\{\mathrm{1}}\end{pmatrix}+\begin{pmatrix}{{n}}\\{\mathrm{2}}\end{pmatrix}+…+\begin{pmatrix}{\:\:\:{n}}\\{{n}−\mathrm{1}}\end{pmatrix}+\begin{pmatrix}{{n}}\\{{n}}\end{pmatrix}=\mathrm{2}^{{n}} \\ $$$${If}\:{n}\in\mathbb{E}^{+} ,\:{say}\:{n}=\mathrm{2}{k} \\ $$$$\begin{pmatrix}{\mathrm{2}{k}}\\{\mathrm{0}}\end{pmatrix}+\begin{pmatrix}{\mathrm{2}{k}}\\{\mathrm{1}}\end{pmatrix}+\begin{pmatrix}{\mathrm{2}{k}}\\{\mathrm{2}}\end{pmatrix}+…+\begin{pmatrix}{\:\:\:\mathrm{2}{k}}\\{\mathrm{2}{k}−\mathrm{1}}\end{pmatrix}+\begin{pmatrix}{\mathrm{2}{k}}\\{\mathrm{2}{k}}\end{pmatrix}=\mathrm{2}^{\mathrm{2}{k}} \\ $$$${Half}\:{of}\:{the}\:{above}\:{series} \\ $$$$\begin{pmatrix}{\mathrm{2}{k}}\\{\mathrm{0}}\end{pmatrix}+\begin{pmatrix}{\mathrm{2}{k}}\\{\mathrm{1}}\end{pmatrix}+\begin{pmatrix}{\mathrm{2}{k}}\\{\mathrm{2}}\end{pmatrix}+…\begin{pmatrix}{\mathrm{2}{k}}\\{{k}−\mathrm{1}}\end{pmatrix}+\begin{pmatrix}{\:\mathrm{2}{k}}\\{\:{k}}\end{pmatrix}−\frac{\mathrm{1}}{\mathrm{2}}\begin{pmatrix}{\mathrm{2}{k}}\\{{k}}\end{pmatrix}=\mathrm{2}^{\mathrm{2}{k}−\mathrm{1}} \\ $$$$\begin{pmatrix}{\mathrm{2}{k}}\\{\:\mathrm{1}}\end{pmatrix}+\begin{pmatrix}{\mathrm{2}{k}}\\{\:\:\mathrm{2}}\end{pmatrix}+…\begin{pmatrix}{\mathrm{2}{k}}\\{{k}−\mathrm{1}}\end{pmatrix}+\begin{pmatrix}{\:\mathrm{2}{k}}\\{\:{k}}\end{pmatrix}=\mathrm{2}^{\mathrm{2}{k}−\mathrm{1}} −\begin{pmatrix}{\mathrm{2}{k}}\\{\mathrm{0}}\end{pmatrix}+\frac{\mathrm{1}}{\mathrm{2}}\begin{pmatrix}{\mathrm{2}{k}}\\{{k}}\end{pmatrix} \\ $$$${Here}\:\mathrm{2}{k}=\mathrm{2014} \\ $$$$\left(\underset{\mathrm{1}} {\overset{\mathrm{2014}} {\:}}\right)\:+\:\left(\underset{\mathrm{2}} {\overset{\mathrm{2014}} {\:}}\right)\:+\:\left(\underset{\mathrm{3}} {\overset{\mathrm{2014}} {\:}}\right)\:+\:\ldots+\:\left(\underset{\mathrm{1007}} {\overset{\mathrm{2014}} {\:}}\right)=\mathrm{2}^{\mathrm{2014}−\mathrm{1}} −\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\begin{pmatrix}{\mathrm{2014}}\\{\mathrm{2008}}\end{pmatrix} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}^{\mathrm{2013}} −\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\begin{pmatrix}{\mathrm{2014}}\\{\mathrm{2007}}\end{pmatrix} \\ $$
Commented by Tawa11 last updated on 25/Dec/21
Great sir.
$$\mathrm{Great}\:\mathrm{sir}. \\ $$
Commented by naka3546 last updated on 25/Dec/21
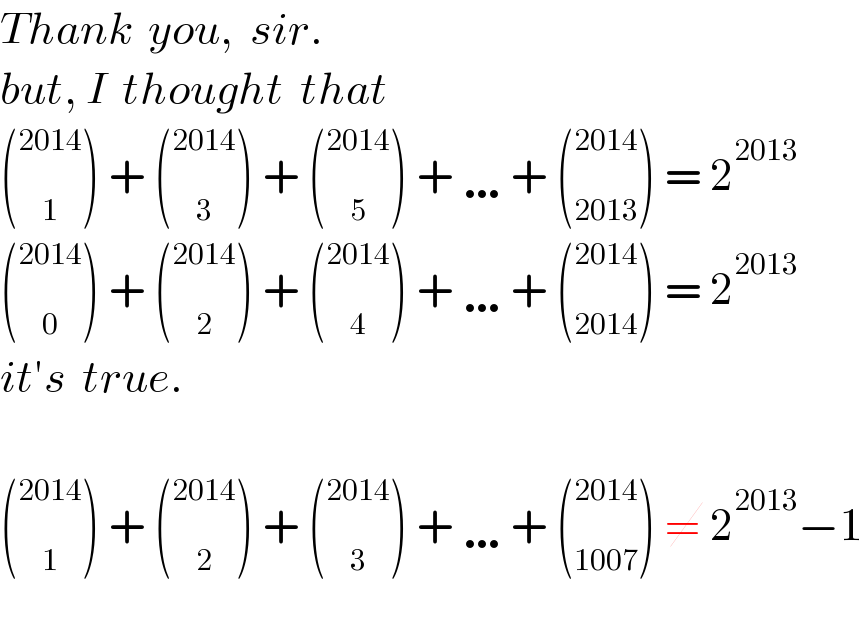
Thank you, sir. but, I thought that ( _1 ^(2014) ) + ( _3 ^(2014) ) + ( _5 ^(2014) ) + …+ ( _(2013) ^(2014) ) = 2^(2013) ( _0 ^(2014) ) + ( _2 ^(2014) ) + ( _4 ^(2014) ) + …+ ( _(2014) ^(2014) ) = 2^(2013) it′s true. ( _1 ^(2014) ) + ( _2 ^(2014) ) + ( _3 ^(2014) ) + …+ ( _(1007) ^(2014) ) ≠ 2^(2013) −1
$${Thank}\:\:{you},\:\:{sir}. \\ $$$${but},\:{I}\:\:{thought}\:\:{that} \\ $$$$\left(\underset{\mathrm{1}} {\overset{\mathrm{2014}} {\:}}\right)\:+\:\left(\underset{\mathrm{3}} {\overset{\mathrm{2014}} {\:}}\right)\:+\:\left(\underset{\mathrm{5}} {\overset{\mathrm{2014}} {\:}}\right)\:+\:\ldots+\:\left(\underset{\mathrm{2013}} {\overset{\mathrm{2014}} {\:}}\right)\:=\:\mathrm{2}^{\mathrm{2013}} \\ $$$$\left(\underset{\mathrm{0}} {\overset{\mathrm{2014}} {\:}}\right)\:+\:\left(\underset{\mathrm{2}} {\overset{\mathrm{2014}} {\:}}\right)\:+\:\left(\underset{\mathrm{4}} {\overset{\mathrm{2014}} {\:}}\right)\:+\:\ldots+\:\left(\underset{\mathrm{2014}} {\overset{\mathrm{2014}} {\:}}\right)\:=\:\mathrm{2}^{\mathrm{2013}} \\ $$$${it}'{s}\:\:{true}. \\ $$$$ \\ $$$$\left(\underset{\mathrm{1}} {\overset{\mathrm{2014}} {\:}}\right)\:+\:\left(\underset{\mathrm{2}} {\overset{\mathrm{2014}} {\:}}\right)\:+\:\left(\underset{\mathrm{3}} {\overset{\mathrm{2014}} {\:}}\right)\:+\:\ldots+\:\left(\underset{\mathrm{1007}} {\overset{\mathrm{2014}} {\:}}\right)\:\neq\:\mathrm{2}^{\mathrm{2013}} −\mathrm{1} \\ $$$$ \\ $$
Commented by Rasheed.Sindhi last updated on 26/Dec/21
naka sir, you′re right! Actually I thought that (a+b)^n ,where n is even has n terms in its expansion whereas in fact it has n+1 terms! Now I′m going to correct my answer!
$${naka}\:{sir},\:{you}'{re}\:{right}! \\ $$$${Actually}\:{I}\:{thought}\:{that}\:\left({a}+{b}\right)^{{n}} ,{where} \\ $$$${n}\:{is}\:{even}\:{has}\:{n}\:{terms}\:{in}\:{its}\:{expansion} \\ $$$${whereas}\:\:{in}\:{fact}\:{it}\:{has}\:{n}+\mathrm{1}\:{terms}! \\ $$$${Now}\:{I}'{m}\:{going}\:{to}\:{correct}\:{my}\:{answer}! \\ $$
Answered by mr W last updated on 26/Dec/21
((n),(k) ) = ((n),((n−k)) ) S= (((2014)),(1) )+ (((2014)),(2) )+ (((2014)),(3) )+... (((2014)),((1006)) )+ (((2014)),((1007)) ) S= (((2014)),((2013)) )+ (((2014)),((2012)) )+ (((2014)),((2011)) )+...+ (((2014)),((1008)) )+ (((2014)),((1007)) ) 2S= (((2014)),(1) )+ (((2014)),(2) )+ (((2014)),(3) )+... (((2014)),((1006)) )+ (((2014)),((1007)) ) + (((2014)),((1008)) )+ (((2014)),((1009)) )+ (((2014)),((1010)) )+...+ (((2014)),((2013)) )+ (((2014)),((1007)) ) 2S+2= (((2014)),(0) )+ (((2014)),(1) )+ (((2014)),(2) )+...+ (((2014)),((2013)) )+ (((2014)),((2014)) )+ (((2014)),((1007)) ) 2S+2=2^(2014) + (((2014)),((1007)) ) ⇒S=2^(2013) +(1/2) (((2014)),((1007)) )−1
$$\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}\:=\begin{pmatrix}{{n}}\\{{n}−{k}}\end{pmatrix} \\ $$$${S}=\begin{pmatrix}{\mathrm{2014}}\\{\mathrm{1}}\end{pmatrix}+\begin{pmatrix}{\mathrm{2014}}\\{\mathrm{2}}\end{pmatrix}+\begin{pmatrix}{\mathrm{2014}}\\{\mathrm{3}}\end{pmatrix}+…\begin{pmatrix}{\mathrm{2014}}\\{\mathrm{1006}}\end{pmatrix}+\begin{pmatrix}{\mathrm{2014}}\\{\mathrm{1007}}\end{pmatrix} \\ $$$${S}=\begin{pmatrix}{\mathrm{2014}}\\{\mathrm{2013}}\end{pmatrix}+\begin{pmatrix}{\mathrm{2014}}\\{\mathrm{2012}}\end{pmatrix}+\begin{pmatrix}{\mathrm{2014}}\\{\mathrm{2011}}\end{pmatrix}+…+\begin{pmatrix}{\mathrm{2014}}\\{\mathrm{1008}}\end{pmatrix}+\begin{pmatrix}{\mathrm{2014}}\\{\mathrm{1007}}\end{pmatrix} \\ $$$$ \\ $$$$\mathrm{2}{S}=\begin{pmatrix}{\mathrm{2014}}\\{\mathrm{1}}\end{pmatrix}+\begin{pmatrix}{\mathrm{2014}}\\{\mathrm{2}}\end{pmatrix}+\begin{pmatrix}{\mathrm{2014}}\\{\mathrm{3}}\end{pmatrix}+…\begin{pmatrix}{\mathrm{2014}}\\{\mathrm{1006}}\end{pmatrix}+\begin{pmatrix}{\mathrm{2014}}\\{\mathrm{1007}}\end{pmatrix} \\ $$$$\:\:\:\:\:\:+\begin{pmatrix}{\mathrm{2014}}\\{\mathrm{1008}}\end{pmatrix}+\begin{pmatrix}{\mathrm{2014}}\\{\mathrm{1009}}\end{pmatrix}+\begin{pmatrix}{\mathrm{2014}}\\{\mathrm{1010}}\end{pmatrix}+…+\begin{pmatrix}{\mathrm{2014}}\\{\mathrm{2013}}\end{pmatrix}+\begin{pmatrix}{\mathrm{2014}}\\{\mathrm{1007}}\end{pmatrix} \\ $$$$\mathrm{2}{S}+\mathrm{2}=\begin{pmatrix}{\mathrm{2014}}\\{\mathrm{0}}\end{pmatrix}+\begin{pmatrix}{\mathrm{2014}}\\{\mathrm{1}}\end{pmatrix}+\begin{pmatrix}{\mathrm{2014}}\\{\mathrm{2}}\end{pmatrix}+…+\begin{pmatrix}{\mathrm{2014}}\\{\mathrm{2013}}\end{pmatrix}+\begin{pmatrix}{\mathrm{2014}}\\{\mathrm{2014}}\end{pmatrix}+\begin{pmatrix}{\mathrm{2014}}\\{\mathrm{1007}}\end{pmatrix} \\ $$$$\mathrm{2}{S}+\mathrm{2}=\mathrm{2}^{\mathrm{2014}} +\begin{pmatrix}{\mathrm{2014}}\\{\mathrm{1007}}\end{pmatrix} \\ $$$$\Rightarrow{S}=\mathrm{2}^{\mathrm{2013}} +\frac{\mathrm{1}}{\mathrm{2}}\begin{pmatrix}{\mathrm{2014}}\\{\mathrm{1007}}\end{pmatrix}−\mathrm{1} \\ $$
Commented by naka3546 last updated on 25/Dec/21
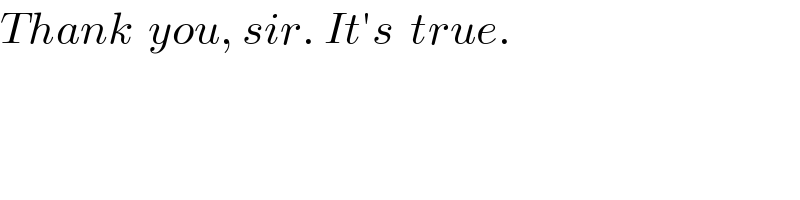
Thank you, sir. It′s true.
$${Thank}\:\:{you},\:{sir}.\:{It}'{s}\:\:{true}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *