Question Number 56104 by problem solverd last updated on 10/Mar/19
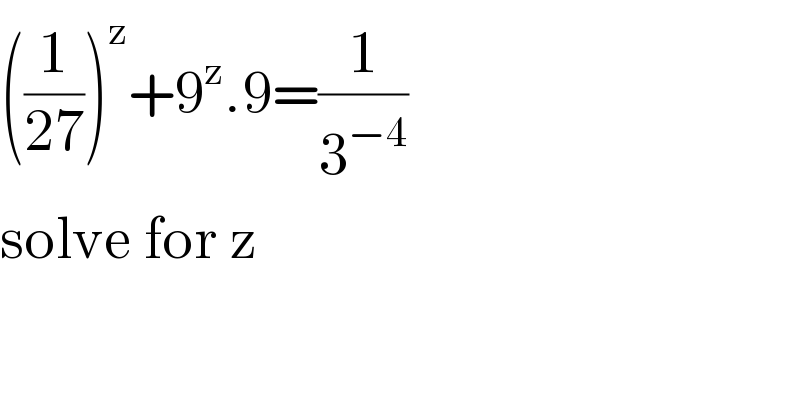
$$\left(\frac{\mathrm{1}}{\mathrm{27}}\right)^{\mathrm{z}} +\mathrm{9}^{\mathrm{z}} .\mathrm{9}=\frac{\mathrm{1}}{\mathrm{3}^{−\mathrm{4}} } \\ $$$$\mathrm{solve}\:\mathrm{for}\:\mathrm{z} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 10/Mar/19

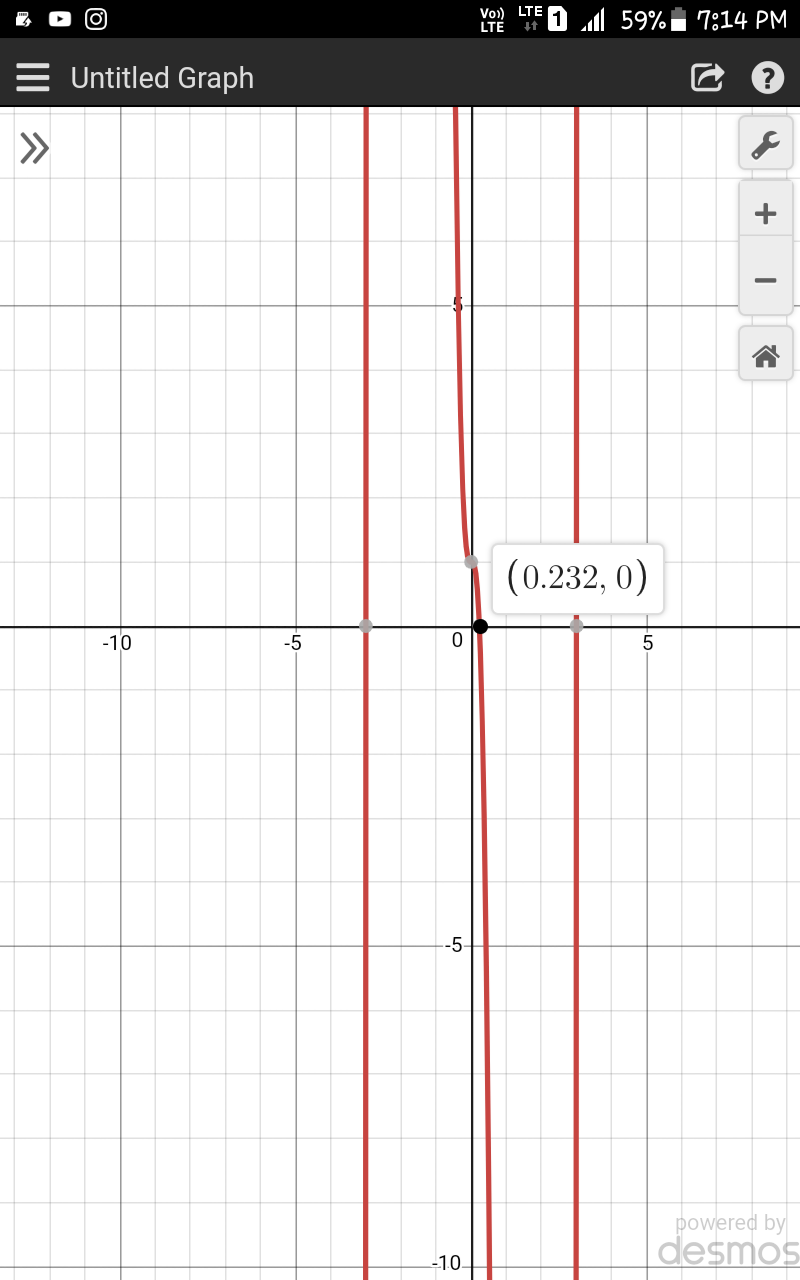
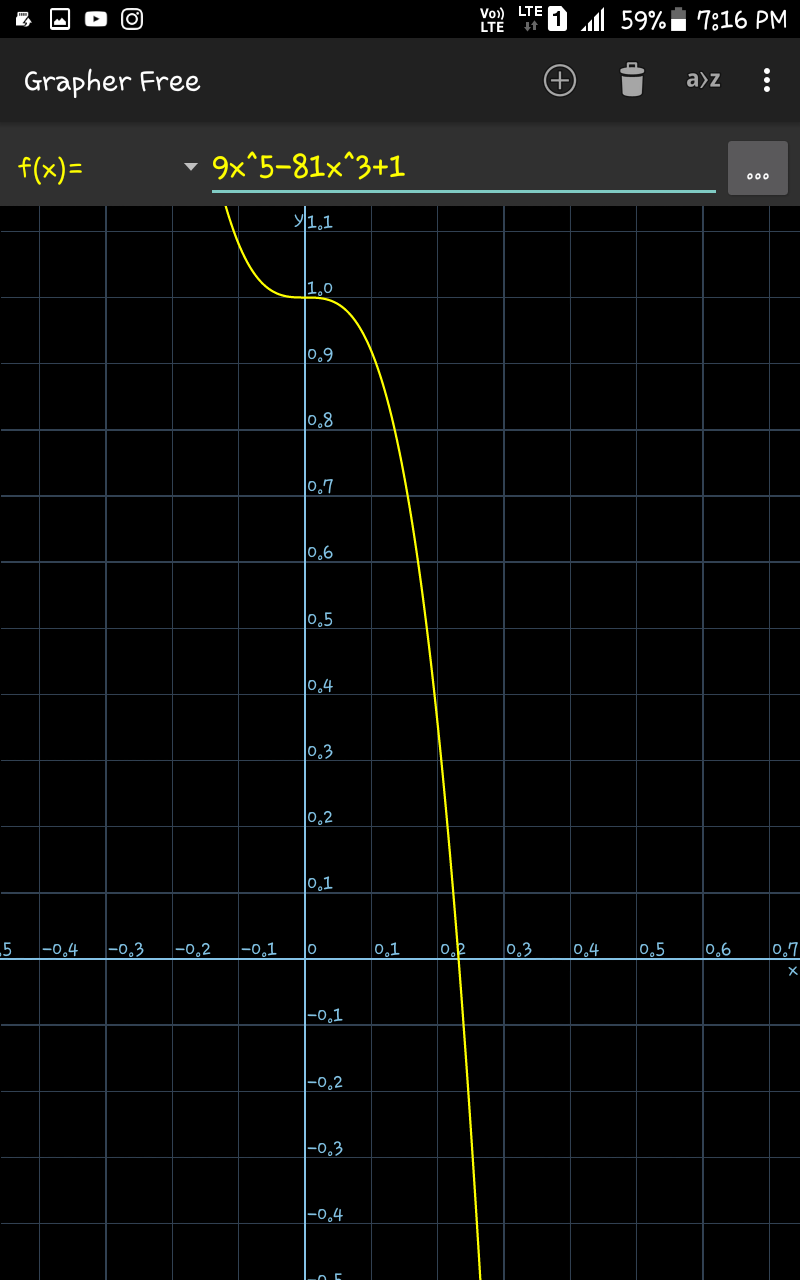
$$\mathrm{3}^{−\mathrm{3}{z}} +\mathrm{3}^{\mathrm{2}{z}+\mathrm{2}} =\mathrm{3}^{\mathrm{4}} \\ $$$$\mathrm{3}^{{z}} ={a} \\ $$$$\frac{\mathrm{1}}{{a}^{\mathrm{3}} }+{a}^{\mathrm{2}} ×\mathrm{9}=\mathrm{81} \\ $$$$\mathrm{9}{a}^{\mathrm{5}} −\mathrm{81}{a}^{\mathrm{3}} +\mathrm{1}=\mathrm{0} \\ $$$${f}\left({a}\right)=\mathrm{9}{a}^{\mathrm{5}} −\mathrm{81}{a}^{\mathrm{3}} +\mathrm{1} \\ $$$${f}\left(\mathrm{0}\right)>\mathrm{0} \\ $$$${f}\left(\mathrm{1}\right)<\mathrm{0} \\ $$$${so}\:{one}\:{root}\:{of}\:{eqn}\:{lies}\:{between}\:\left(\mathrm{0},\mathrm{1}\right) \\ $$$${now}\:{using}\:{graph}\:{finding}\:{the}\:{value}… \\ $$$${a}=\mathrm{0}.\mathrm{2316} \\ $$$$\mathrm{3}^{{z}} =\mathrm{0}.\mathrm{2316}\:\:\: \\ $$$$ \\ $$$$ \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 10/Mar/19
Commented by tanmay.chaudhury50@gmail.com last updated on 10/Mar/19
Commented by problem solverd last updated on 11/Mar/19
$$\mathrm{sir}\:\mathrm{which}\:\mathrm{programe}\:\mathrm{used}\:\mathrm{for}\:\mathrm{drawing}\:\mathrm{graph}? \\ $$
Answered by MJS last updated on 10/Mar/19
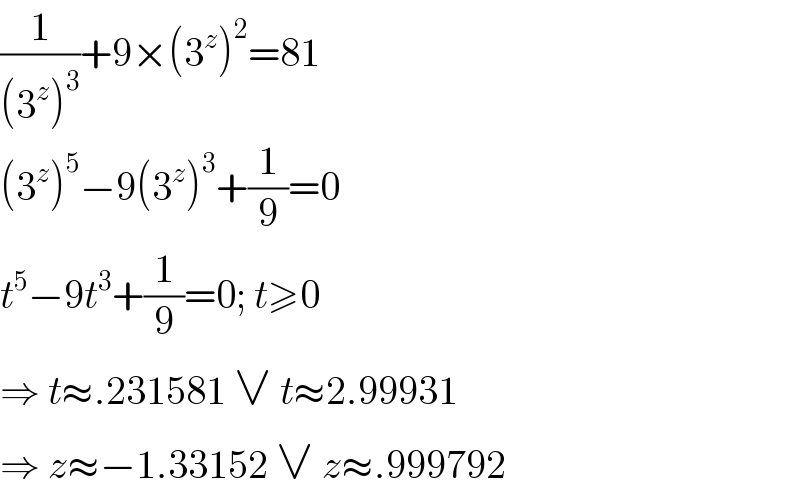
$$\frac{\mathrm{1}}{\left(\mathrm{3}^{{z}} \right)^{\mathrm{3}} }+\mathrm{9}×\left(\mathrm{3}^{{z}} \right)^{\mathrm{2}} =\mathrm{81} \\ $$$$\left(\mathrm{3}^{{z}} \right)^{\mathrm{5}} −\mathrm{9}\left(\mathrm{3}^{{z}} \right)^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{9}}=\mathrm{0} \\ $$$${t}^{\mathrm{5}} −\mathrm{9}{t}^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{9}}=\mathrm{0};\:{t}\geqslant\mathrm{0} \\ $$$$\Rightarrow\:{t}\approx.\mathrm{231581}\:\vee\:{t}\approx\mathrm{2}.\mathrm{99931} \\ $$$$\Rightarrow\:{z}\approx−\mathrm{1}.\mathrm{33152}\:\vee\:{z}\approx.\mathrm{999792} \\ $$
