Question Number 43481 by kumar123 last updated on 11/Sep/18

$$\frac{\left(\mathrm{1}+\mathrm{2}{i}\right)^{\mathrm{3}} }{\left(\mathrm{3}+{i}\right)}= \\ $$
Answered by Joel578 last updated on 11/Sep/18
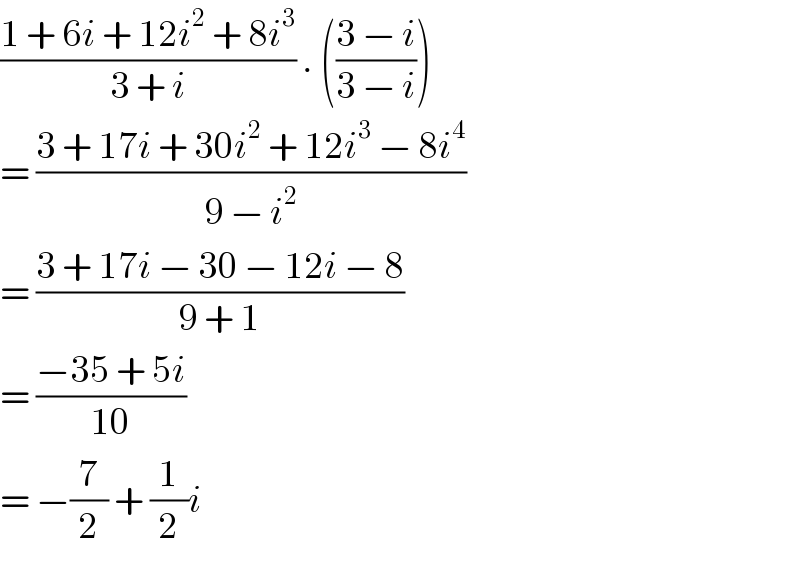
$$\frac{\mathrm{1}\:+\:\mathrm{6}{i}\:+\:\mathrm{12}{i}^{\mathrm{2}} \:+\:\mathrm{8}{i}^{\mathrm{3}} }{\mathrm{3}\:+\:{i}}\:.\:\left(\frac{\mathrm{3}\:−\:{i}}{\mathrm{3}\:−\:{i}}\right) \\ $$$$=\:\frac{\mathrm{3}\:+\:\mathrm{17}{i}\:+\:\mathrm{30}{i}^{\mathrm{2}} \:+\:\mathrm{12}{i}^{\mathrm{3}} \:−\:\mathrm{8}{i}^{\mathrm{4}} }{\mathrm{9}\:−\:{i}^{\mathrm{2}} } \\ $$$$=\:\frac{\mathrm{3}\:+\:\mathrm{17}{i}\:−\:\mathrm{30}\:−\:\mathrm{12}{i}\:−\:\mathrm{8}}{\mathrm{9}\:+\:\mathrm{1}} \\ $$$$=\:\frac{−\mathrm{35}\:+\:\mathrm{5}{i}}{\mathrm{10}} \\ $$$$=\:−\frac{\mathrm{7}}{\mathrm{2}}\:+\:\frac{\mathrm{1}}{\mathrm{2}}{i} \\ $$
