Question Number 27611 by NECx last updated on 10/Jan/18
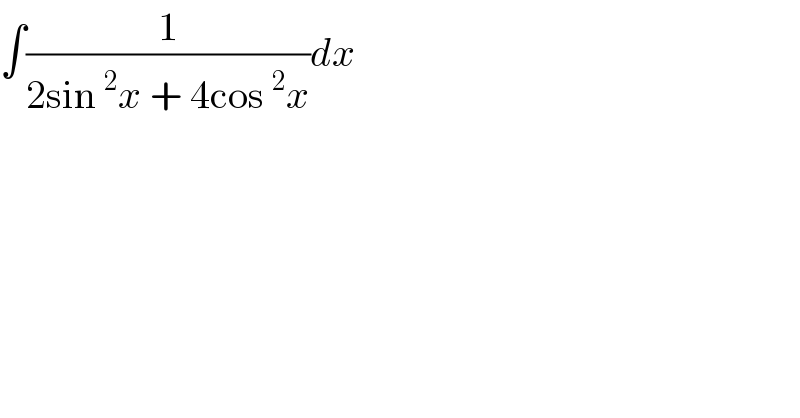
$$\int\frac{\mathrm{1}}{\mathrm{2sin}\:^{\mathrm{2}} {x}\:+\:\mathrm{4cos}\:^{\mathrm{2}} {x}}{dx} \\ $$
Answered by ajfour last updated on 11/Jan/18

$$=\int\frac{\mathrm{sec}\:^{\mathrm{2}} {xdx}}{\mathrm{2tan}\:^{\mathrm{2}} {x}+\mathrm{4}}=\int\frac{{dt}}{\mathrm{2}{t}^{\mathrm{2}} +\mathrm{4}}\:\:;\left({t}=\mathrm{tan}\:{x}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dt}}{{t}^{\mathrm{2}} +\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{tan}\:{x}}{\:\sqrt{\mathrm{2}}}\right)+{c}\:. \\ $$
