1-2sin-4x-lt-cos-2-4x-solve-

Question Number 57357 by ANTARES VY last updated on 03/Apr/19

1 - 2 \sin (4 x) < \cos^{2} (4 x)

solve .

Commented by bshahid010@gmail.com last updated on 03/Apr/19

1 - 2 \sin (4 x) < \cos^{2} (4 x)

1 - 2 \sin (4 x) - \cos^{2} (4 x) < 0

1 - 2 \sin (4 x) - 1 + \sin^{2} (4 x) < 0

\sin^{2} 4 x - 2 \sin 4 x < 0

\sin 4 x (\sin 4 x - 2) < 0

\sin 4 x \in (0, 2) so \sin 4 x \in (0, 1)

x \in (0, \sin 1)

Commented by tanmay.chaudhury50@gmail.com last updated on 03/Apr/19

m a x v a l u e o f s i n θ = 1

s o i t h i n k s i n 4 x \in (0, 1) b u t

s i n 4 x \notin (0, 2)

l e t o t h e r c o m m e n t \dots

Answered by tanmay.chaudhury50@gmail.com last updated on 03/Apr/19

s i n 4 x = a

1 - 2 a < 1 - a^{2}

a^{2} - 2 a < 0

a (a - 2) < 0

a \neq 2 a_{m a x} = 1

1 > a > 0 i s t h e r e a u i r e d s o l u t i o n

1 > s i n 4 x > 0

s i n \frac{π}{2} > s i n 4 x > s i n 0

\frac{π}{8} > x > 0

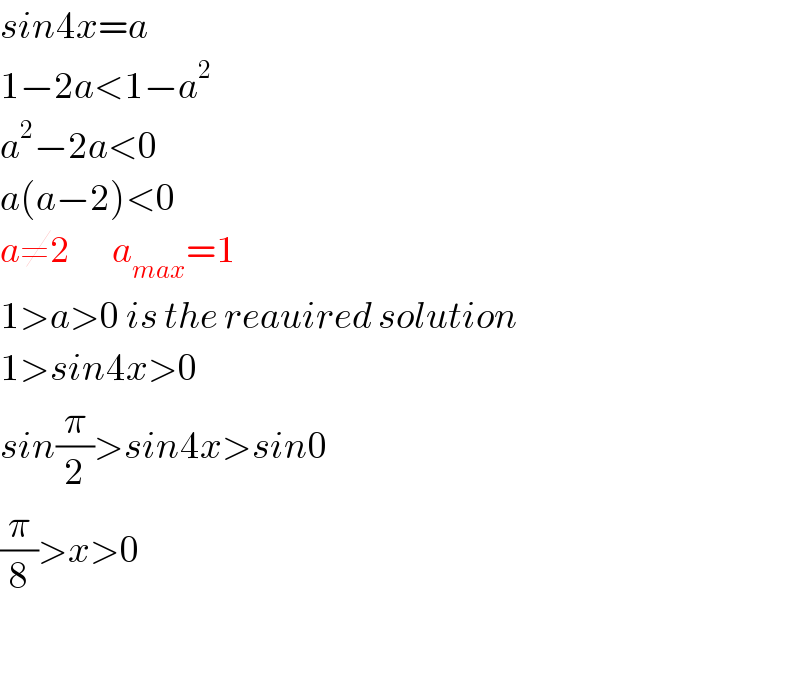
Commented by ANTARES VY last updated on 03/Apr/19

? ? ?

Answered by einsteindrmaths@hotmail.fr last updated on 03/Apr/19

c os^{2} (4 x) = 1 - {s i n}^{2} (4 x) ====> 1 - \sin (4 x) < 1 - {s i n}^{2} (4 x)

==> {s i n}^{2} (4 x) - s i n (4 x) < 0 ==> s i n (4 x) (1 - s i n (4 x)) < 0 ==>

s i n (4 x) > 0 & 1 - s i n (4 x) \neq 0 ===> x \neq {\frac{π}{8} + \frac{k π}{2} / k \in I Z} \cup] \frac{k π}{2}; \frac{(2 k + 1) π}{4} [

Answered by mr W last updated on 03/Apr/19

1 - 2 \sin (4 x) < 1 - \sin^{2} (4 x)

\sin (4 x) {\sin (4 x) - 2} < 0

s i n c e \sin (4 x) - 2 < 0

\Rightarrow \sin (4 x) > 0

o r

\Rightarrow 0 < \sin (4 x) ⩽ 1

\Rightarrow 4 x \in (2 n π, 2 n π + π)

\Rightarrow x \in (\frac{n π}{2}, \frac{n π}{2} + \frac{π}{4}) w i t h n \in W

Facebook Tweet Pin