Question Number 95888 by i jagooll last updated on 28/May/20
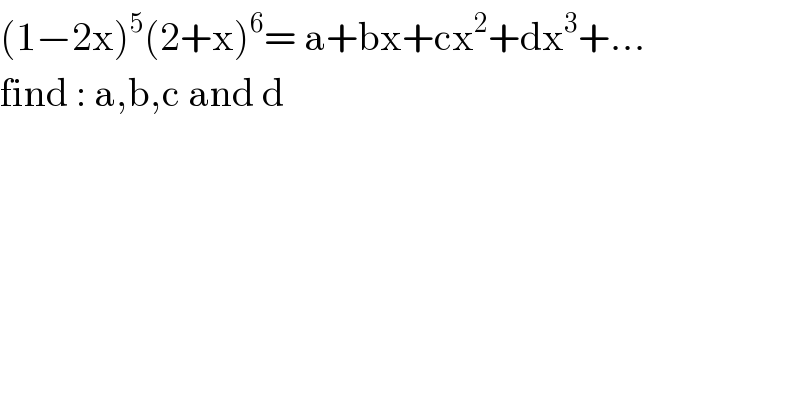
$$\left(\mathrm{1}−\mathrm{2x}\right)^{\mathrm{5}} \left(\mathrm{2}+\mathrm{x}\right)^{\mathrm{6}} =\:\mathrm{a}+\mathrm{bx}+\mathrm{cx}^{\mathrm{2}} +\mathrm{dx}^{\mathrm{3}} +… \\ $$$$\mathrm{find}\::\:\mathrm{a},\mathrm{b},\mathrm{c}\:\mathrm{and}\:\mathrm{d}\: \\ $$
Answered by john santu last updated on 28/May/20

$$\Rightarrow\left(\mathrm{2}+\mathrm{x}\right)\:\underset{\mathrm{k}\:=\:\mathrm{0}} {\overset{\mathrm{5}} {\sum}}\mathrm{C}\left(\mathrm{5},\mathrm{k}\right)\:\left(\mathrm{2}\right)^{\mathrm{5}−\mathrm{k}} \:\left(−\left(\mathrm{3x}+\mathrm{2x}^{\mathrm{2}} \right)\right)^{\mathrm{k}} \\ $$$$\mathrm{clearly}\:\mathrm{a}\:=\:\mathrm{64}\: \\ $$$$\mathrm{term}\:\mathrm{containing}\:\:\mathrm{x}\:\Rightarrow\left(\mathrm{2}+\mathrm{x}\right)\mathrm{C}\left(\mathrm{5},\mathrm{1}\right)\:\mathrm{2}^{\mathrm{4}} \:\left(−\mathrm{3x}−\mathrm{2x}^{\mathrm{2}} \right)\: \\ $$$$=\:\mathrm{80}\left(\mathrm{2}+\mathrm{x}\right)\left(−\mathrm{3x}−\mathrm{2x}^{\mathrm{2}} \right)\: \\ $$$$=\:−\mathrm{480x}−\mathrm{560x}^{\mathrm{2}} −\mathrm{160x}^{\mathrm{3}} \\ $$$$\mathrm{so}\:\mathrm{b}\:=\:−\mathrm{480} \\ $$$$\mathrm{term}\:\mathrm{containing}\:\mathrm{x}^{\mathrm{2}} \\ $$$$=\:\left(\mathrm{2}+\mathrm{x}\right)\mathrm{C}\left(\mathrm{5},\mathrm{2}\right)\:\mathrm{2}^{\mathrm{3}} \:\left(\mathrm{3x}+\mathrm{2x}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$=\:\mathrm{80}\left(\mathrm{2}+\mathrm{x}\right)\left(\mathrm{9x}^{\mathrm{2}} +\mathrm{12x}^{\mathrm{3}} +\mathrm{4x}^{\mathrm{4}} \right) \\ $$$$\mathrm{so}\:\mathrm{term}\:\mathrm{x}^{\mathrm{2}} \:=\:\mathrm{560x}^{\mathrm{2}} +\mathrm{1440x}^{\mathrm{2}} \\ $$$$\mathrm{then}\:\mathrm{we}\:\mathrm{get}\:\mathrm{c}\:=\:\mathrm{2000} \\ $$$$\mathrm{term}\:\mathrm{containing}\:\mathrm{x}^{\mathrm{3}} \\ $$$$=\:\left(\mathrm{2}+\mathrm{x}\right)\:\mathrm{C}\left(\mathrm{5},\mathrm{3}\right)\:\mathrm{2}^{\mathrm{2}\:} \left(−\mathrm{3x}−\mathrm{2x}^{\mathrm{2}} \right)^{\mathrm{3}} \\ $$$$=\:\mathrm{40}\left(\mathrm{2}+\mathrm{x}\right)\left(−\mathrm{27x}^{\mathrm{3}} +…\right) \\ $$$$=\:−\mathrm{2160x}^{\mathrm{3}} +… \\ $$$$\mathrm{so}\:\mathrm{term}\:\mathrm{x}^{\mathrm{3}} \:=\:−\mathrm{160x}^{\mathrm{3}} +\mathrm{1920x}^{\mathrm{3}} +\mathrm{720x}^{\mathrm{3}} −\mathrm{2160x}^{\mathrm{3}} \\ $$$$=\:\mathrm{320x}^{\mathrm{3}} \\ $$$$\mathrm{then}\:\mathrm{d}\:=\:\mathrm{320} \\ $$$$ \\ $$
