Menu Close

1-2x-y-y-1-y-2x-y-6-

Tinku Tara 0 Comments
Pin




Question Number 100954 by bobhans last updated on 29/Jun/20
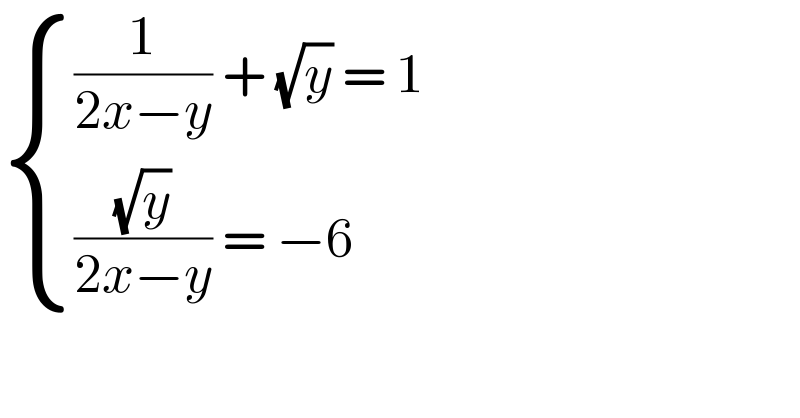
{ (((1/(2x−y)) + (√y) = 1)),((((√y)/(2x−y)) = −6)) :}
$$\begin{cases}{\frac{\mathrm{1}}{\mathrm{2}{x}−{y}}\:+\:\sqrt{{y}}\:=\:\mathrm{1}}\\{\frac{\sqrt{{y}}}{\mathrm{2}{x}−{y}}\:=\:−\mathrm{6}}\end{cases} \\ $$
Commented by Dwaipayan Shikari last updated on 29/Jun/20
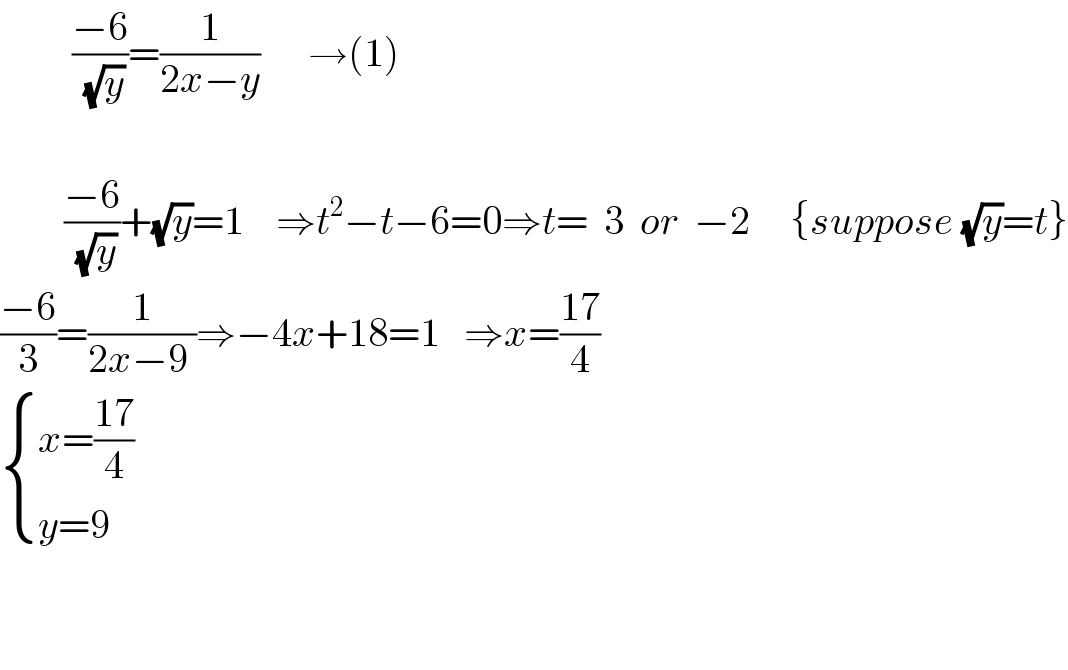
((−6)/( (√y)))=(1/(2x−y)) →(1) ((−6)/( (√y)))+(√y)=1 ⇒t^2 −t−6=0⇒t= 3 or −2 {suppose (√y)=t} ((−6)/3)=(1/(2x−9 ))⇒−4x+18=1 ⇒x=((17)/4) { ((x=((17)/4))),((y=9)) :}
$$\:\:\:\:\:\:\:\:\:\frac{−\mathrm{6}}{\:\sqrt{{y}}}=\frac{\mathrm{1}}{\mathrm{2}{x}−{y}}\:\:\:\:\:\:\rightarrow\left(\mathrm{1}\right) \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\frac{−\mathrm{6}}{\:\sqrt{{y}}}+\sqrt{{y}}=\mathrm{1}\:\:\:\:\Rightarrow{t}^{\mathrm{2}} −{t}−\mathrm{6}=\mathrm{0}\Rightarrow{t}=\:\:\mathrm{3}\:\:{or}\:\:−\mathrm{2}\:\:\:\:\:\left\{{suppose}\:\sqrt{{y}}={t}\right\} \\ $$$$\frac{−\mathrm{6}}{\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{2}{x}−\mathrm{9}\:}\Rightarrow−\mathrm{4}{x}+\mathrm{18}=\mathrm{1}\:\:\:\Rightarrow{x}=\frac{\mathrm{17}}{\mathrm{4}}\:\: \\ $$$$\begin{cases}{{x}=\frac{\mathrm{17}}{\mathrm{4}}}\\{{y}=\mathrm{9}}\end{cases} \\ $$$$ \\ $$$$ \\ $$
Answered by ajfour last updated on 29/Jun/20
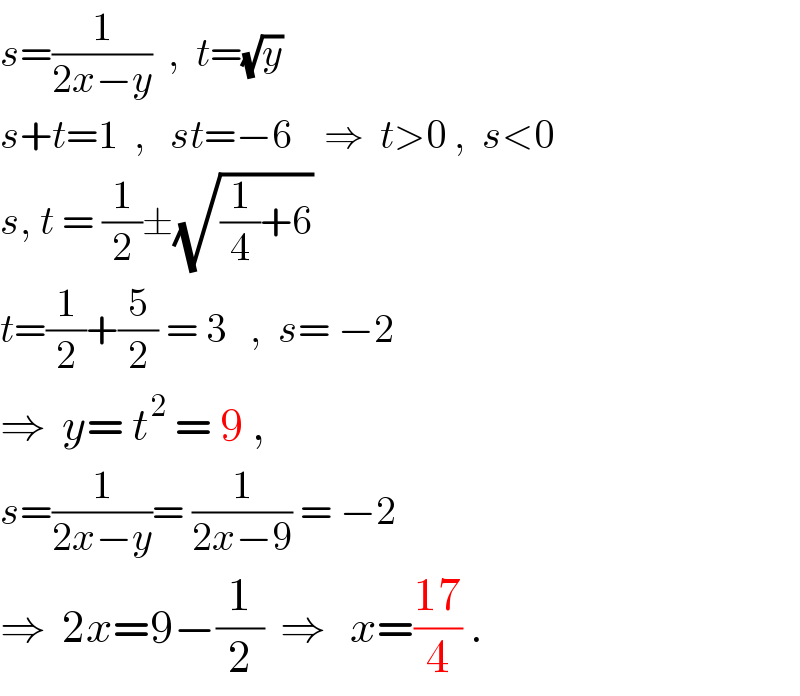
s=(1/(2x−y)) , t=(√y) s+t=1 , st=−6 ⇒ t>0 , s<0 s, t = (1/2)±(√((1/4)+6)) t=(1/2)+(5/2) = 3 , s= −2 ⇒ y= t^2 = 9 , s=(1/(2x−y))= (1/(2x−9)) = −2 ⇒ 2x=9−(1/2) ⇒ x=((17)/4) .
$${s}=\frac{\mathrm{1}}{\mathrm{2}{x}−{y}}\:\:,\:\:{t}=\sqrt{{y}} \\ $$$${s}+{t}=\mathrm{1}\:\:,\:\:\:{st}=−\mathrm{6}\:\:\:\:\Rightarrow\:\:{t}>\mathrm{0}\:,\:\:{s}<\mathrm{0} \\ $$$${s},\:{t}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\pm\sqrt{\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{6}}\: \\ $$$${t}=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{5}}{\mathrm{2}}\:=\:\mathrm{3}\:\:\:,\:\:{s}=\:−\mathrm{2} \\ $$$$\Rightarrow\:\:{y}=\:{t}^{\mathrm{2}} \:=\:\mathrm{9}\:,\: \\ $$$${s}=\frac{\mathrm{1}}{\mathrm{2}{x}−{y}}=\:\frac{\mathrm{1}}{\mathrm{2}{x}−\mathrm{9}}\:=\:−\mathrm{2} \\ $$$$\Rightarrow\:\:\mathrm{2}{x}=\mathrm{9}−\frac{\mathrm{1}}{\mathrm{2}}\:\:\Rightarrow\:\:\:{x}=\frac{\mathrm{17}}{\mathrm{4}}\:. \\ $$
Answered by john santu last updated on 29/Jun/20
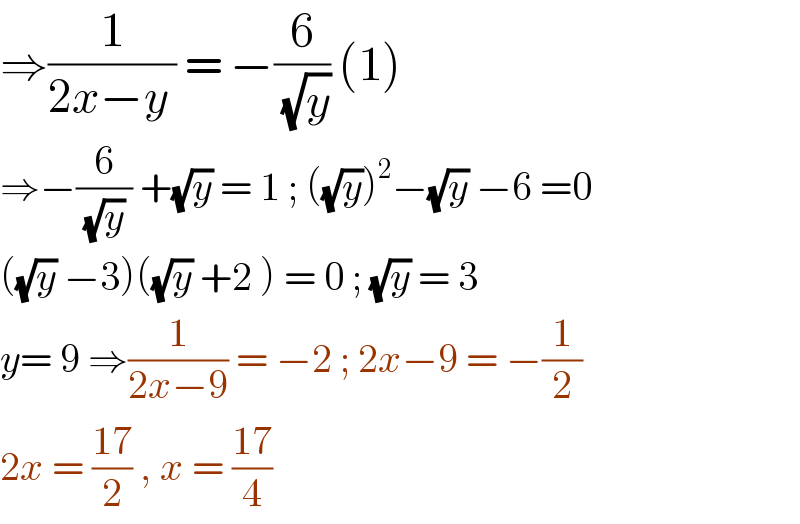
⇒(1/(2x−y )) = −(6/( (√y))) (1) ⇒−(6/( (√y) )) +(√y) = 1 ; ((√y))^2 −(√y) −6 =0 ((√y) −3)((√y) +2 ) = 0 ; (√y) = 3 y= 9 ⇒(1/(2x−9)) = −2 ; 2x−9 = −(1/2) 2x = ((17)/2) , x = ((17)/4)
$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2}{x}−{y}\:}\:=\:−\frac{\mathrm{6}}{\:\sqrt{{y}}}\:\left(\mathrm{1}\right) \\ $$$$\Rightarrow−\frac{\mathrm{6}}{\:\sqrt{{y}}\:}\:+\sqrt{{y}}\:=\:\mathrm{1}\:;\:\left(\sqrt{{y}}\right)^{\mathrm{2}} −\sqrt{{y}}\:−\mathrm{6}\:=\mathrm{0} \\ $$$$\left(\sqrt{{y}}\:−\mathrm{3}\right)\left(\sqrt{{y}}\:+\mathrm{2}\:\right)\:=\:\mathrm{0}\:;\:\sqrt{{y}}\:=\:\mathrm{3} \\ $$$${y}=\:\mathrm{9}\:\Rightarrow\frac{\mathrm{1}}{\mathrm{2}{x}−\mathrm{9}}\:=\:−\mathrm{2}\:;\:\mathrm{2}{x}−\mathrm{9}\:=\:−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{2}{x}\:=\:\frac{\mathrm{17}}{\mathrm{2}}\:,\:{x}\:=\:\frac{\mathrm{17}}{\mathrm{4}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *