Question Number 96117 by bobhans last updated on 30/May/20
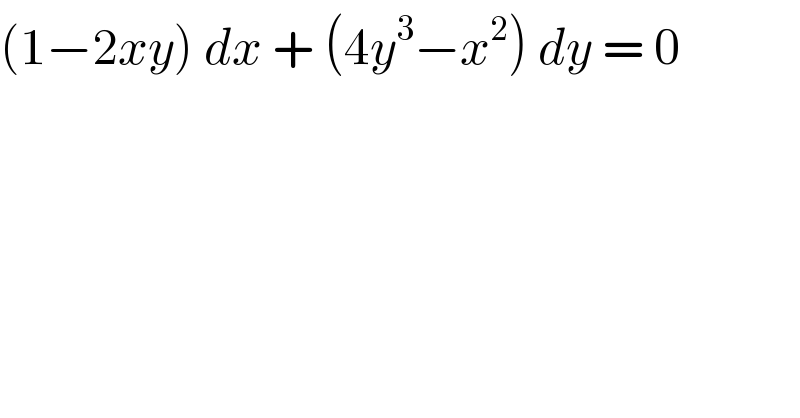
$$\left(\mathrm{1}−\mathrm{2}{xy}\right)\:{dx}\:+\:\left(\mathrm{4}{y}^{\mathrm{3}} −{x}^{\mathrm{2}} \right)\:{dy}\:=\:\mathrm{0}\: \\ $$
Answered by john santu last updated on 30/May/20
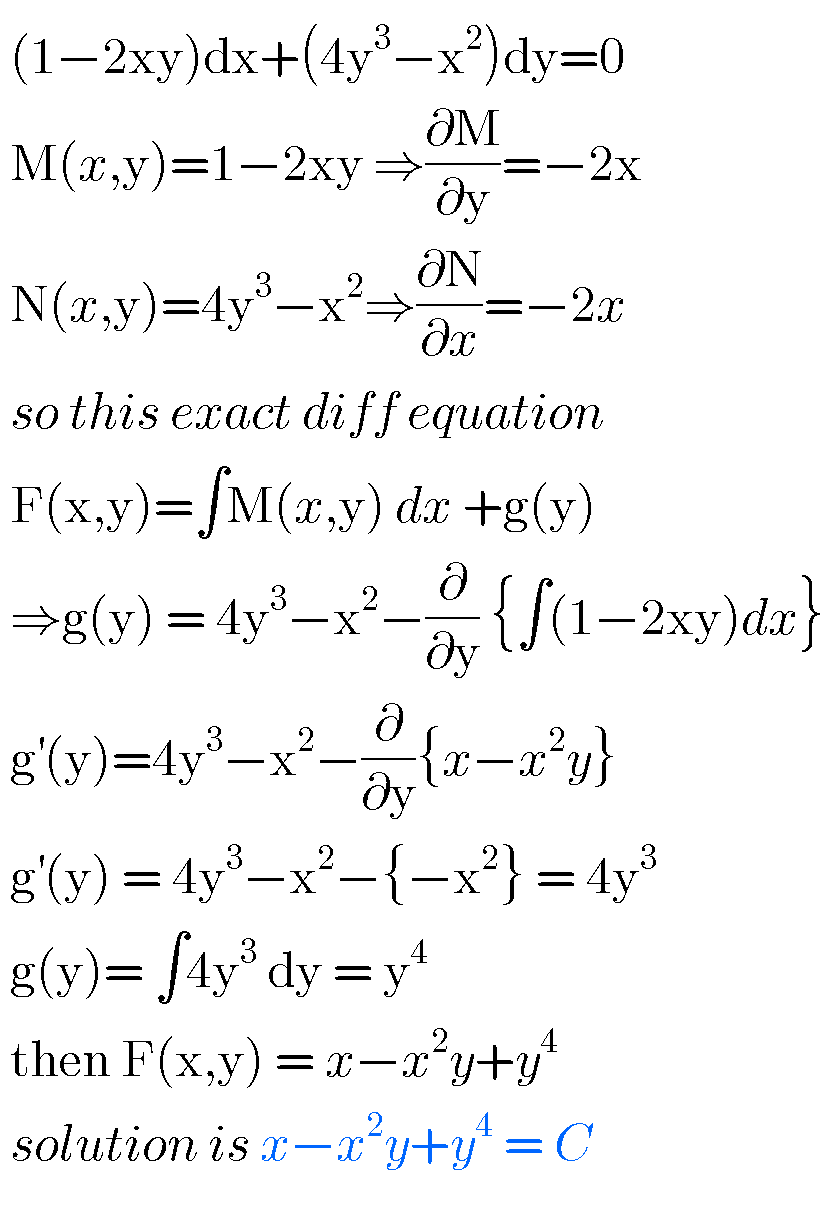
Commented by john santu last updated on 30/May/20
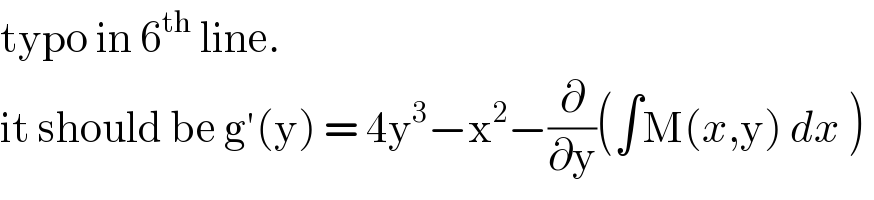
$$\mathrm{typo}\:\mathrm{in}\:\mathrm{6}^{\mathrm{th}} \:\mathrm{line}. \\ $$$$\mathrm{it}\:\mathrm{should}\:\mathrm{be}\:\mathrm{g}'\left(\mathrm{y}\right)\:=\:\mathrm{4y}^{\mathrm{3}} −\mathrm{x}^{\mathrm{2}} −\frac{\partial}{\partial\mathrm{y}}\left(\int\mathrm{M}\left({x},\mathrm{y}\right)\:{dx}\:\right)\: \\ $$
Commented by bobhans last updated on 30/May/20

$$\mathrm{thank}\:\mathrm{you} \\ $$
Commented by i jagooll last updated on 30/May/20
yeahhh
Commented by Tinku Tara last updated on 02/Jun/20
$$\mathrm{Hi}\:\mathrm{jagooll} \\ $$$$\mathrm{Are}\:\mathrm{you}\:\mathrm{able}\:\mathrm{to}\:\mathrm{post}\:\mathrm{questions} \\ $$$$\mathrm{now}. \\ $$
Answered by bemath last updated on 30/May/20
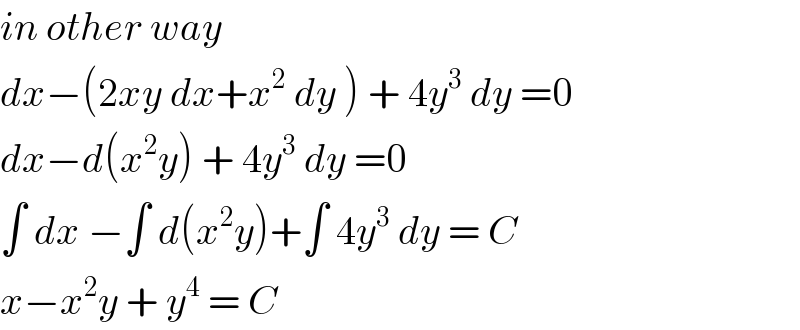
$${in}\:{other}\:{way}\: \\ $$$${dx}−\left(\mathrm{2}{xy}\:{dx}+{x}^{\mathrm{2}} \:{dy}\:\right)\:+\:\mathrm{4}{y}^{\mathrm{3}} \:{dy}\:=\mathrm{0} \\ $$$${dx}−{d}\left({x}^{\mathrm{2}} {y}\right)\:+\:\mathrm{4}{y}^{\mathrm{3}} \:{dy}\:=\mathrm{0} \\ $$$$\int\:{dx}\:−\int\:{d}\left({x}^{\mathrm{2}} {y}\right)+\int\:\mathrm{4}{y}^{\mathrm{3}} \:{dy}\:=\:{C} \\ $$$${x}−{x}^{\mathrm{2}} {y}\:+\:{y}^{\mathrm{4}} \:=\:{C}\: \\ $$
