Question Number 101808 by Ar Brandon last updated on 04/Jul/20
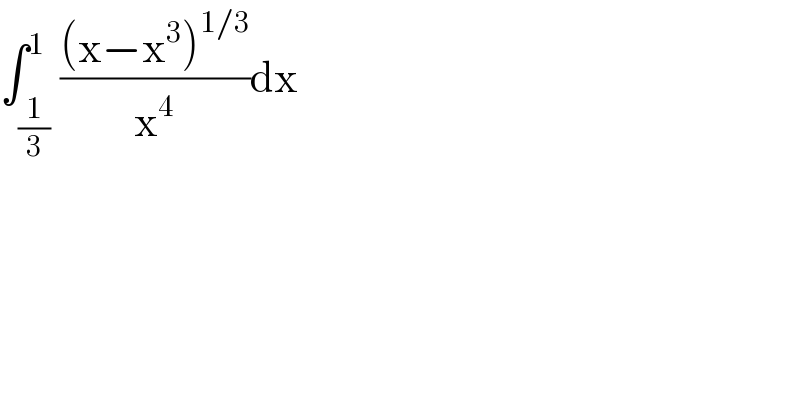
$$\int_{\frac{\mathrm{1}}{\mathrm{3}}} ^{\mathrm{1}} \frac{\left(\mathrm{x}−\mathrm{x}^{\mathrm{3}} \right)^{\mathrm{1}/\mathrm{3}} }{\mathrm{x}^{\mathrm{4}} }\mathrm{dx} \\ $$
Answered by Dwaipayan Shikari last updated on 04/Jul/20
![∫_(1/3) ^1 ((x((1/x^2 )−1)^(1/3) dx)/x^4 )=−(1/2)∫_(1/3) ^1 ((−2)/x^3 )((1/x^2 )−1)^(1/3) dx=(1/2)∫_0 ^8 t^(1/3) dt=(3/8)[t^(4/3) ]_0 ^8 =6 {Assuming ((1/x^2 )−1)=t](https://www.tinkutara.com/question/Q101810.png)
$$\int_{\frac{\mathrm{1}}{\mathrm{3}}} ^{\mathrm{1}} \frac{{x}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} {dx}}{{x}^{\mathrm{4}} }=−\frac{\mathrm{1}}{\mathrm{2}}\int_{\frac{\mathrm{1}}{\mathrm{3}}} ^{\mathrm{1}} \frac{−\mathrm{2}}{{x}^{\mathrm{3}} }\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} {dx}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{8}} {t}^{\frac{\mathrm{1}}{\mathrm{3}}} {dt}=\frac{\mathrm{3}}{\mathrm{8}}\left[{t}^{\frac{\mathrm{4}}{\mathrm{3}}} \right]_{\mathrm{0}} ^{\mathrm{8}} =\mathrm{6} \\ $$$$\:\:\:\left\{{Assuming}\:\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\mathrm{1}\right)={t}\right. \\ $$
Commented by Ar Brandon last updated on 04/Jul/20
Cool ��
Commented by Dwaipayan Shikari last updated on 04/Jul/20
����
Answered by bobhans last updated on 05/Jul/20
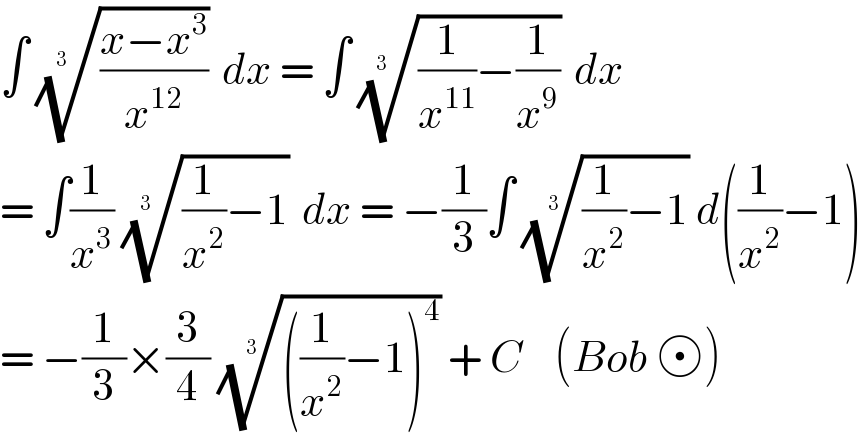
$$\int\:\sqrt[{\mathrm{3}\:\:}]{\frac{{x}−{x}^{\mathrm{3}} }{{x}^{\mathrm{12}} }}\:{dx}\:=\:\int\:\sqrt[{\mathrm{3}\:\:}]{\frac{\mathrm{1}}{{x}^{\mathrm{11}} }−\frac{\mathrm{1}}{{x}^{\mathrm{9}} }}\:{dx} \\ $$$$=\:\int\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\:\sqrt[{\mathrm{3}\:\:}]{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\mathrm{1}}\:{dx}\:=\:−\frac{\mathrm{1}}{\mathrm{3}}\int\:\sqrt[{\mathrm{3}}]{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\mathrm{1}}\:{d}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\mathrm{1}\right) \\ $$$$=\:−\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{3}}{\mathrm{4}}\:\sqrt[{\mathrm{3}}]{\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\mathrm{1}\right)^{\mathrm{4}} }\:+\:{C}\:\:\:\:\left({Bob}\: \right) \\ $$
