Menu Close

1-3-3-1-3-5-3-2-1-3-5-7-3-3-a-b-a-b-Z-

Tinku Tara 0 Comments
Pin




Question Number 62556 by naka3546 last updated on 22/Jun/19
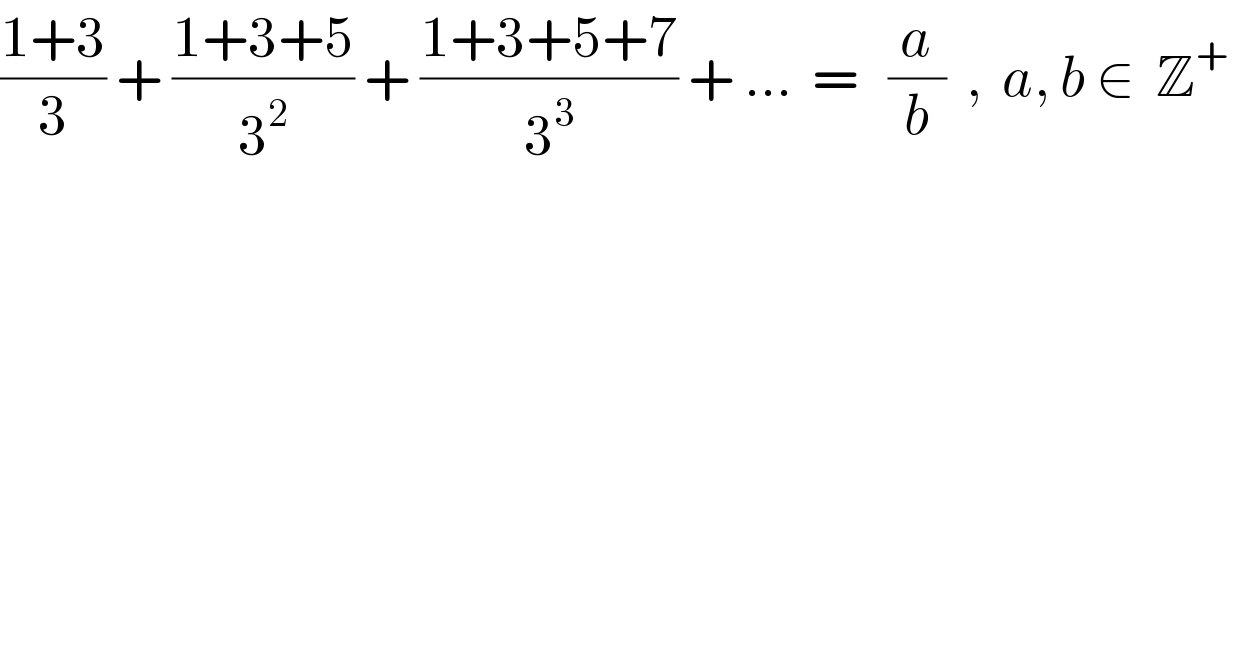
((1+3)/3) + ((1+3+5)/3^2 ) + ((1+3+5+7)/3^3 ) + ... = (a/b) , a, b ∈ Z^+
$$\frac{\mathrm{1}+\mathrm{3}}{\mathrm{3}}\:+\:\frac{\mathrm{1}+\mathrm{3}+\mathrm{5}}{\mathrm{3}^{\mathrm{2}} }\:+\:\frac{\mathrm{1}+\mathrm{3}+\mathrm{5}+\mathrm{7}}{\mathrm{3}^{\mathrm{3}} }\:+\:…\:\:=\:\:\:\frac{{a}}{{b}}\:\:,\:\:{a},\:{b}\:\in\:\:\mathbb{Z}^{+} \: \\ $$
Commented by Prithwish sen last updated on 22/Jun/19
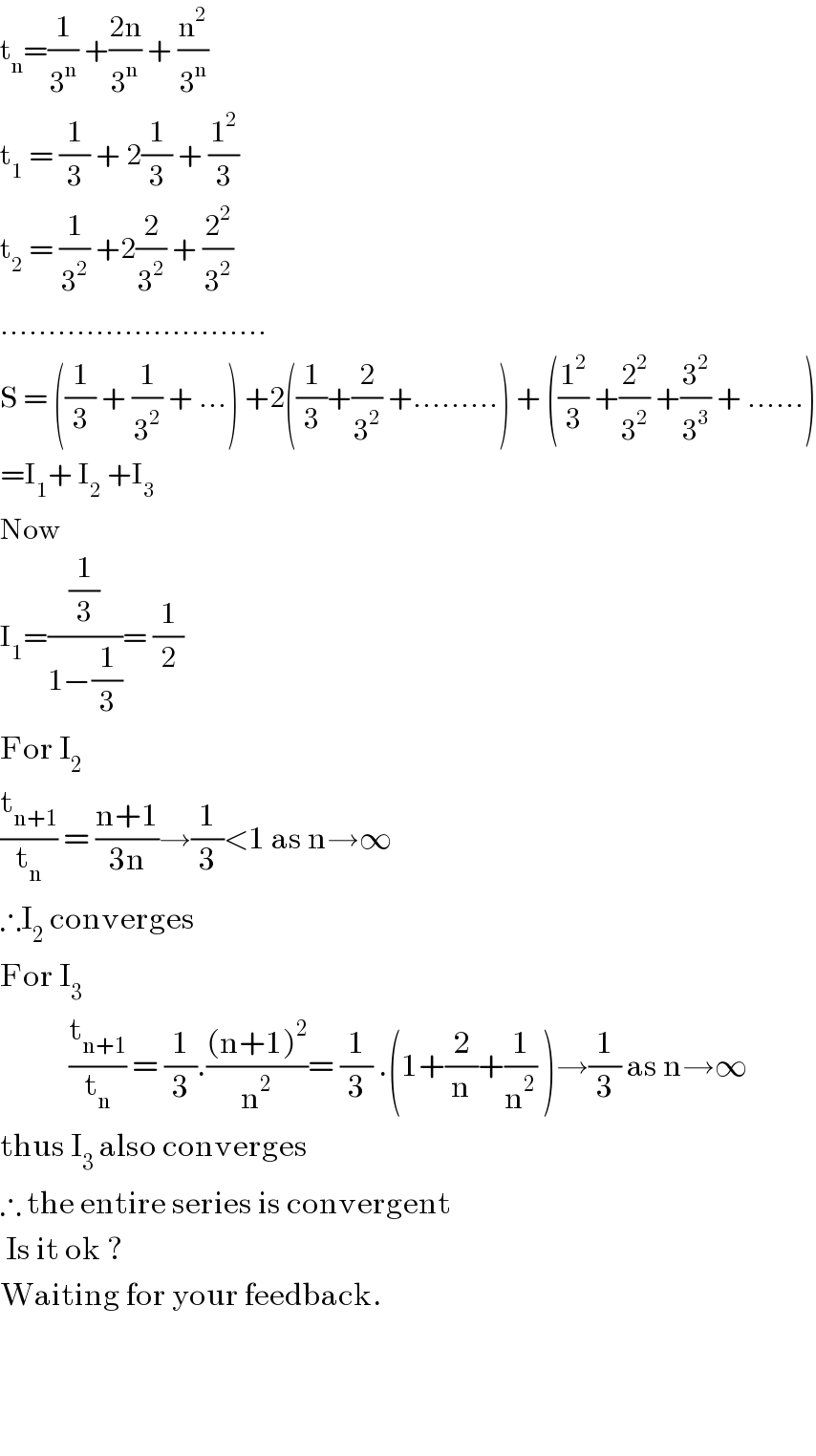
t_n =(1/3^n ) +((2n)/3^n ) + (n^2 /3^n ) t_1 = (1/3) + 2(1/3) + (1^2 /3) t_2 = (1/3^2 ) +2(2/3^2 ) + (2^2 /3^2 ) ............................ S = ((1/3) + (1/3^2 ) + ...) +2((1/3)+(2/3^2 ) +.........) + ((1^2 /3) +(2^2 /3^2 ) +(3^2 /3^3 ) + ......) =I_1 + I_2 +I_3 Now I_1 =((1/3)/(1−(1/3)))= (1/2) For I_2 (t_(n+1) /t_n ) = ((n+1)/(3n))→(1/3)<1 as n→∞ ∴I_2 converges For I_3 (t_(n+1) /t_n ) = (1/3).(((n+1)^2 )/n^2 )= (1/3) .(1+(2/n)+(1/n^2 ) )→(1/3) as n→∞ thus I_3 also converges ∴ the entire series is convergent Is it ok ? Waiting for your feedback.
$$\mathrm{t}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{n}} }\:+\frac{\mathrm{2n}}{\mathrm{3}^{\mathrm{n}} }\:+\:\frac{\mathrm{n}^{\mathrm{2}} }{\mathrm{3}^{\mathrm{n}} } \\ $$$$\mathrm{t}_{\mathrm{1}} \:=\:\frac{\mathrm{1}}{\mathrm{3}}\:+\:\mathrm{2}\frac{\mathrm{1}}{\mathrm{3}}\:+\:\frac{\mathrm{1}^{\mathrm{2}} }{\mathrm{3}} \\ $$$$\mathrm{t}_{\mathrm{2}} \:=\:\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }\:+\mathrm{2}\frac{\mathrm{2}}{\mathrm{3}^{\mathrm{2}} }\:+\:\frac{\mathrm{2}^{\mathrm{2}} }{\mathrm{3}^{\mathrm{2}} } \\ $$$$………………………. \\ $$$$\mathrm{S}\:=\:\left(\frac{\mathrm{1}}{\mathrm{3}}\:+\:\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }\:+\:…\right)\:+\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{2}}{\mathrm{3}^{\mathrm{2}} }\:+………\right)\:+\:\left(\frac{\mathrm{1}^{\mathrm{2}} }{\mathrm{3}}\:+\frac{\mathrm{2}^{\mathrm{2}} }{\mathrm{3}^{\mathrm{2}} }\:+\frac{\mathrm{3}^{\mathrm{2}} }{\mathrm{3}^{\mathrm{3}} }\:+\:……\right) \\ $$$$=\mathrm{I}_{\mathrm{1}} +\:\mathrm{I}_{\mathrm{2}} \:+\mathrm{I}_{\mathrm{3}} \\ $$$$\mathrm{Now}\: \\ $$$$\mathrm{I}_{\mathrm{1}} =\frac{\frac{\mathrm{1}}{\mathrm{3}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}}=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{For}\:\mathrm{I}_{\mathrm{2}} \\ $$$$\frac{\mathrm{t}_{\mathrm{n}+\mathrm{1}} }{\mathrm{t}_{\mathrm{n}} }\:=\:\frac{\mathrm{n}+\mathrm{1}}{\mathrm{3n}}\rightarrow\frac{\mathrm{1}}{\mathrm{3}}<\mathrm{1}\:\mathrm{as}\:\mathrm{n}\rightarrow\infty \\ $$$$\therefore\mathrm{I}_{\mathrm{2}} \:\mathrm{converges} \\ $$$$\mathrm{For}\:\mathrm{I}_{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{t}_{\mathrm{n}+\mathrm{1}} }{\mathrm{t}_{\mathrm{n}} }\:=\:\frac{\mathrm{1}}{\mathrm{3}}.\frac{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{n}^{\mathrm{2}} }=\:\frac{\mathrm{1}}{\mathrm{3}}\:.\left(\mathrm{1}+\frac{\mathrm{2}}{\mathrm{n}}+\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\:\right)\rightarrow\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{as}\:\mathrm{n}\rightarrow\infty \\ $$$$\mathrm{thus}\:\mathrm{I}_{\mathrm{3}} \:\mathrm{also}\:\mathrm{converges} \\ $$$$\therefore\:\mathrm{the}\:\mathrm{entire}\:\mathrm{series}\:\mathrm{is}\:\mathrm{convergent} \\ $$$$\:\mathrm{Is}\:\mathrm{it}\:\mathrm{ok}\:? \\ $$$$\mathrm{Waiting}\:\mathrm{for}\:\mathrm{your}\:\mathrm{feedback}. \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 22/Jun/19
S =Σ_(n=1) ^∞ ((Σ_(k=0) ^n (2k+1))/3^n ) let the sequence u_k =2k+1 is srithmetic with u_0 =1 and r =2 ⇒ Σ_(k=0) ^n u_k =u_0 +u_1 +...+u_n =((n+1)/2)(u_o +u_n )=((n+1)/2)(1+2n+1) =(n+1)^2 ⇒ S =Σ_(n=1) ^∞ (((n+1)^2 )/3^n ) =Σ_(n=2) ^∞ (n^2 /3^(n−1) ) =3 Σ_(n=2) ^∞ (n^2 /3^n ) Σ_(n=2) ^∞ (n^2 /3^n ) =Σ_(n=0) ^∞ (n^2 /3^n ) −(1/3) let w(x) =Σ_(n=0) ^∞ x^n with ∣x∣<1 we have w^′ (x) =Σ_(n=1) ^∞ nx^(n−1) ⇒xw^′ (x) =Σ_(n=1) ^∞ nx^n ⇒w^′ (x)+x w^((2)) (x) =Σ_(n=1) ^∞ n^2 x^(n−1 ) ⇒ x{w^′ (x)+x w^((2)) (x)} =Σ_(n=1) ^∞ n^2 x^n but w(x) =(1/(1−x)) ⇒w^′ (x) =(1/((1−x)^2 )) ⇒ w^((2)) (x) =−((2(−1)(1−x))/((1−x)^4 )) =(2/((1−x)^3 )) ⇒ Σ_(n=1) ^∞ n^2 x^n =x{ (1/((1−x)^2 )) +((2x)/((1−x)^3 ))} =(x/((1−x)^2 )) +((2x^2 )/((1−x)^3 )) =((x(1−x)+2x^2 )/((1−x)^3 )) =((x^2 +x)/((1−x)^3 )) and Σ_(n=1) ^∞ (n^2 /3^n ) =w((1/3)) =(((1/9)+(1/3))/(((2/3))^3 )) =(4/8) =(1/2) ⇒ S =3{(1/2)−(1/3)} =(3/2) − 1 =(1/2)
$${S}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\sum_{{k}=\mathrm{0}} ^{{n}} \:\left(\mathrm{2}{k}+\mathrm{1}\right)}{\mathrm{3}^{{n}} }\:\:{let}\:\:\:{the}\:{sequence}\:{u}_{{k}} =\mathrm{2}{k}+\mathrm{1}\:{is}\:{srithmetic}\:{with}\:{u}_{\mathrm{0}} =\mathrm{1} \\ $$$${and}\:{r}\:=\mathrm{2}\:\Rightarrow\:\sum_{{k}=\mathrm{0}} ^{{n}} \:{u}_{{k}} ={u}_{\mathrm{0}} +{u}_{\mathrm{1}} +…+{u}_{{n}} =\frac{{n}+\mathrm{1}}{\mathrm{2}}\left({u}_{{o}} \:+{u}_{{n}} \right)=\frac{{n}+\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{2}{n}+\mathrm{1}\right) \\ $$$$=\left({n}+\mathrm{1}\right)^{\mathrm{2}} \:\Rightarrow\:{S}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{3}^{{n}} }\:=\sum_{{n}=\mathrm{2}} ^{\infty} \:\frac{{n}^{\mathrm{2}} }{\mathrm{3}^{{n}−\mathrm{1}} }\:=\mathrm{3}\:\sum_{{n}=\mathrm{2}} ^{\infty} \:\frac{{n}^{\mathrm{2}} }{\mathrm{3}^{{n}} } \\ $$$$\sum_{{n}=\mathrm{2}} ^{\infty} \:\frac{{n}^{\mathrm{2}} }{\mathrm{3}^{{n}} }\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{n}^{\mathrm{2}} }{\mathrm{3}^{{n}} }\:−\frac{\mathrm{1}}{\mathrm{3}}\:\:{let}\:{w}\left({x}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:{x}^{{n}} \:\:\:\:\:{with}\:\mid{x}\mid<\mathrm{1}\:\:{we}\:{have}\: \\ $$$${w}^{'} \left({x}\right)\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:{nx}^{{n}−\mathrm{1}} \:\:\Rightarrow{xw}^{'} \left({x}\right)\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:{nx}^{{n}} \:\Rightarrow{w}^{'} \left({x}\right)+{x}\:{w}^{\left(\mathrm{2}\right)} \left({x}\right)\:=\sum_{{n}=\mathrm{1}} ^{\infty} {n}^{\mathrm{2}} \:{x}^{{n}−\mathrm{1}\:} \:\Rightarrow \\ $$$${x}\left\{{w}^{'} \left({x}\right)+{x}\:{w}^{\left(\mathrm{2}\right)} \left({x}\right)\right\}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:{n}^{\mathrm{2}} \:{x}^{{n}} \:\:\:{but}\:{w}\left({x}\right)\:=\frac{\mathrm{1}}{\mathrm{1}−{x}}\:\Rightarrow{w}^{'} \left({x}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$${w}^{\left(\mathrm{2}\right)} \left({x}\right)\:=−\frac{\mathrm{2}\left(−\mathrm{1}\right)\left(\mathrm{1}−{x}\right)}{\left(\mathrm{1}−{x}\right)^{\mathrm{4}} }\:=\frac{\mathrm{2}}{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:{n}^{\mathrm{2}} \:{x}^{{n}} \:={x}\left\{\:\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }\:+\frac{\mathrm{2}{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }\right\}\:=\frac{{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }\:+\frac{\mathrm{2}{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }\:=\frac{{x}\left(\mathrm{1}−{x}\right)+\mathrm{2}{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }\:=\frac{{x}^{\mathrm{2}} \:+{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} } \\ $$$${and}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{n}^{\mathrm{2}} }{\mathrm{3}^{{n}} }\:={w}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\:=\frac{\frac{\mathrm{1}}{\mathrm{9}}+\frac{\mathrm{1}}{\mathrm{3}}}{\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{3}} }\:=\frac{\mathrm{4}}{\mathrm{8}}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\:{S}\:=\mathrm{3}\left\{\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}\right\}\:=\frac{\mathrm{3}}{\mathrm{2}}\:−\:\mathrm{1}\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$
Answered by Smail last updated on 23/Jun/19
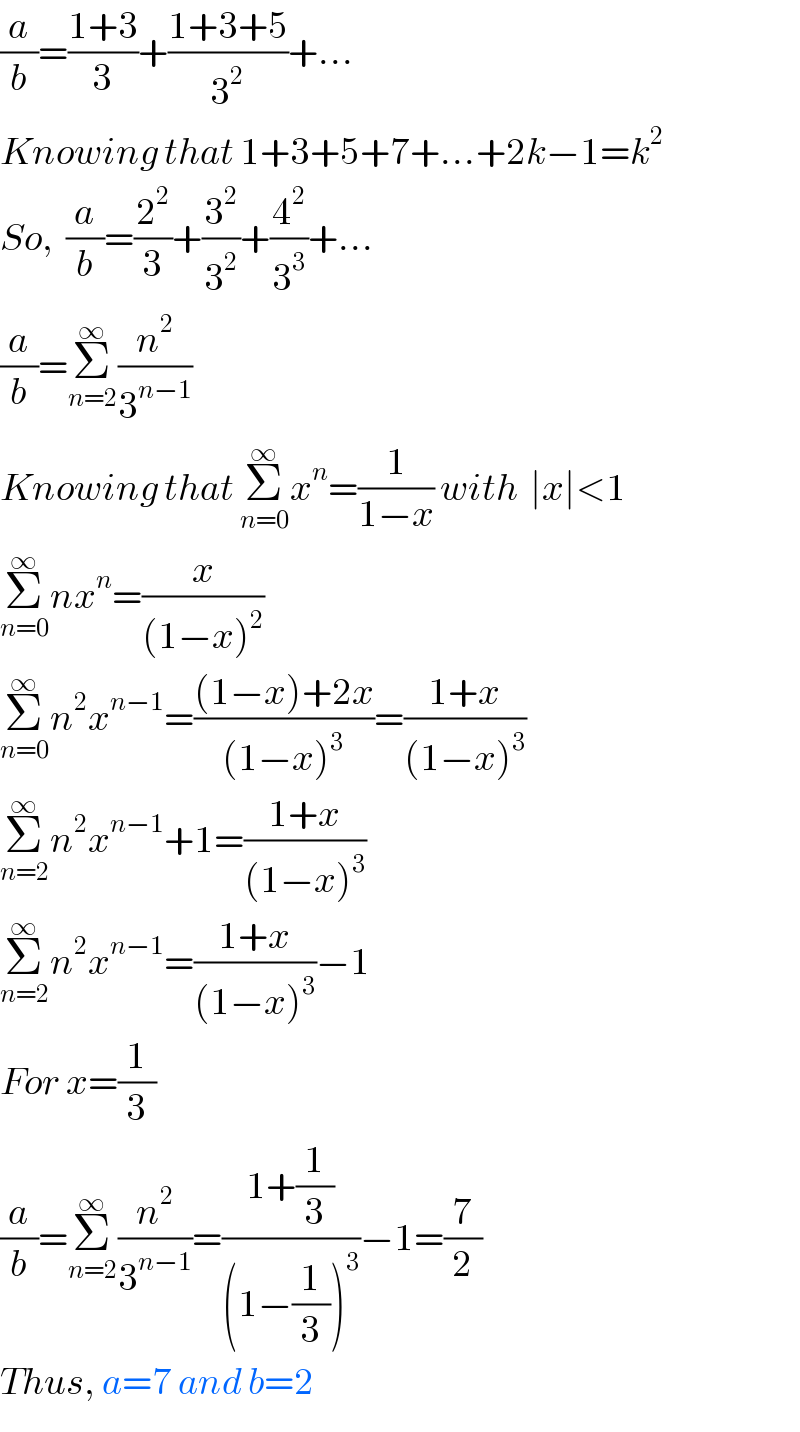
(a/b)=((1+3)/3)+((1+3+5)/3^2 )+... Knowing that 1+3+5+7+...+2k−1=k^2 So, (a/b)=(2^2 /3)+(3^2 /3^2 )+(4^2 /3^3 )+... (a/b)=Σ_(n=2) ^∞ (n^2 /3^(n−1) ) Knowing that Σ_(n=0) ^∞ x^n =(1/(1−x)) with ∣x∣<1 Σ_(n=0) ^∞ nx^n =(x/((1−x)^2 )) Σ_(n=0) ^∞ n^2 x^(n−1) =(((1−x)+2x)/((1−x)^3 ))=((1+x)/((1−x)^3 )) Σ_(n=2) ^∞ n^2 x^(n−1) +1=((1+x)/((1−x)^3 )) Σ_(n=2) ^∞ n^2 x^(n−1) =((1+x)/((1−x)^3 ))−1 For x=(1/3) (a/b)=Σ_(n=2) ^∞ (n^2 /3^(n−1) )=((1+(1/3))/((1−(1/3))^3 ))−1=(7/2) Thus, a=7 and b=2
$$\frac{{a}}{{b}}=\frac{\mathrm{1}+\mathrm{3}}{\mathrm{3}}+\frac{\mathrm{1}+\mathrm{3}+\mathrm{5}}{\mathrm{3}^{\mathrm{2}} }+… \\ $$$${Knowing}\:{that}\:\mathrm{1}+\mathrm{3}+\mathrm{5}+\mathrm{7}+…+\mathrm{2}{k}−\mathrm{1}={k}^{\mathrm{2}} \\ $$$${So},\:\:\frac{{a}}{{b}}=\frac{\mathrm{2}^{\mathrm{2}} }{\mathrm{3}}+\frac{\mathrm{3}^{\mathrm{2}} }{\mathrm{3}^{\mathrm{2}} }+\frac{\mathrm{4}^{\mathrm{2}} }{\mathrm{3}^{\mathrm{3}} }+… \\ $$$$\frac{{a}}{{b}}=\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{{n}^{\mathrm{2}} }{\mathrm{3}^{{n}−\mathrm{1}} } \\ $$$${Knowing}\:{that}\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{x}^{{n}} =\frac{\mathrm{1}}{\mathrm{1}−{x}}\:{with}\:\:\mid{x}\mid<\mathrm{1} \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{nx}^{{n}} =\frac{{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} } \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{n}^{\mathrm{2}} {x}^{{n}−\mathrm{1}} =\frac{\left(\mathrm{1}−{x}\right)+\mathrm{2}{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }=\frac{\mathrm{1}+{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} } \\ $$$$\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}{n}^{\mathrm{2}} {x}^{{n}−\mathrm{1}} +\mathrm{1}=\frac{\mathrm{1}+{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} } \\ $$$$\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}{n}^{\mathrm{2}} {x}^{{n}−\mathrm{1}} =\frac{\mathrm{1}+{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }−\mathrm{1} \\ $$$${For}\:{x}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\frac{{a}}{{b}}=\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{{n}^{\mathrm{2}} }{\mathrm{3}^{{n}−\mathrm{1}} }=\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}}{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{3}} }−\mathrm{1}=\frac{\mathrm{7}}{\mathrm{2}} \\ $$$${Thus},\:{a}=\mathrm{7}\:{and}\:{b}=\mathrm{2} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *