Menu Close

1-3-7-15-30-57-103-x-What-s-x-

Tinku Tara 0 Comments
Pin




Question Number 64903 by naka3546 last updated on 23/Jul/19
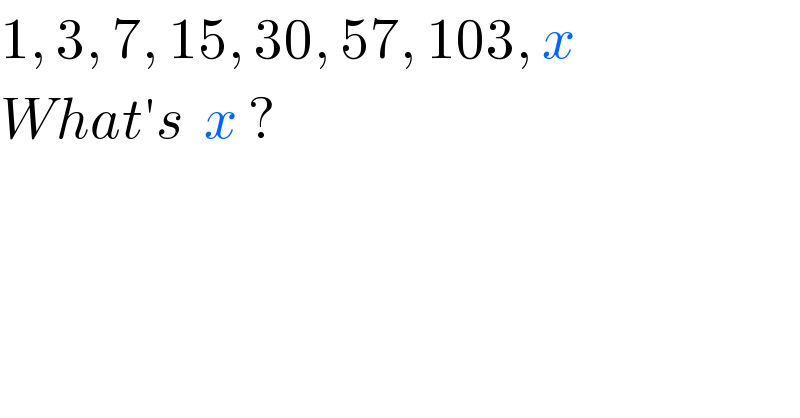
1, 3, 7, 15, 30, 57, 103, x What′s x ?
$$\mathrm{1},\:\mathrm{3},\:\mathrm{7},\:\mathrm{15},\:\mathrm{30},\:\mathrm{57},\:\mathrm{103},\:{x} \\ $$$${What}'{s}\:\:{x}\:? \\ $$
Commented by Tony Lin last updated on 23/Jul/19
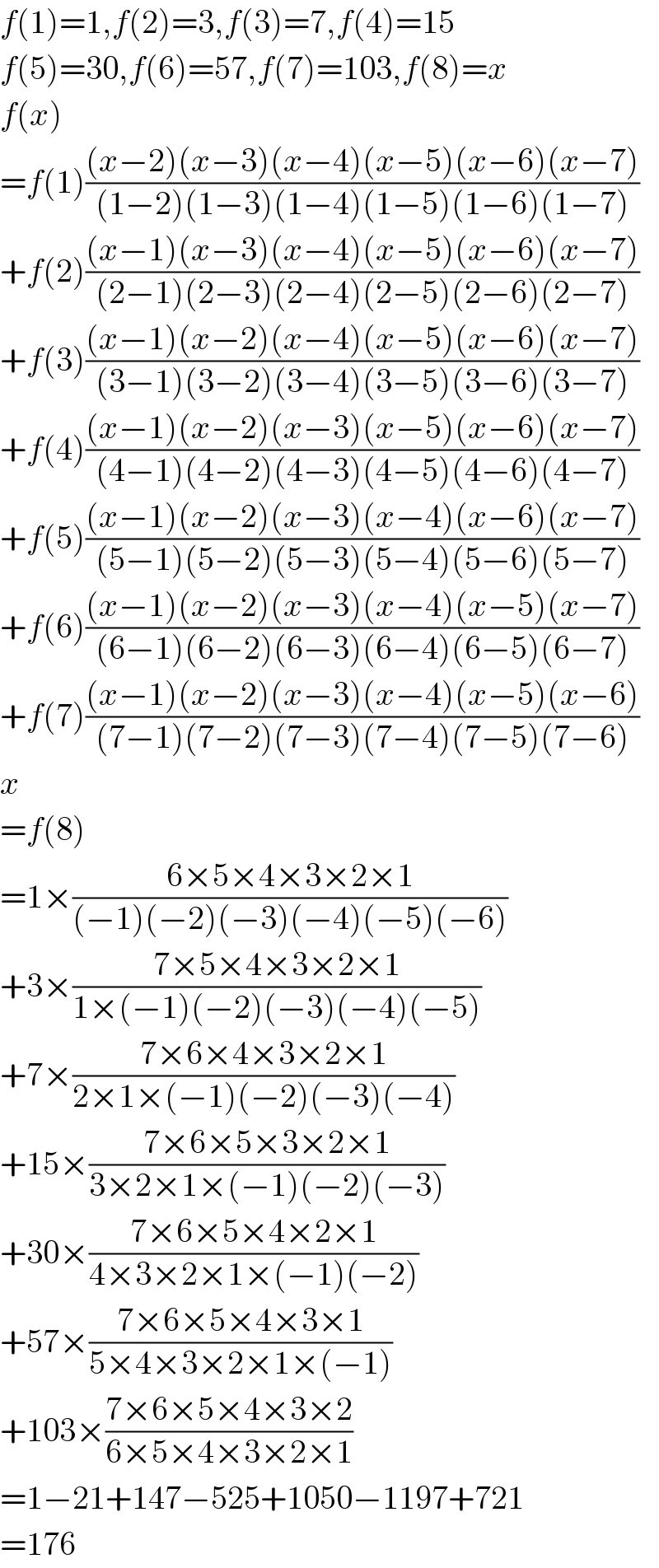
f(1)=1,f(2)=3,f(3)=7,f(4)=15 f(5)=30,f(6)=57,f(7)=103,f(8)=x f(x) =f(1)(((x−2)(x−3)(x−4)(x−5)(x−6)(x−7))/((1−2)(1−3)(1−4)(1−5)(1−6)(1−7))) +f(2)(((x−1)(x−3)(x−4)(x−5)(x−6)(x−7))/((2−1)(2−3)(2−4)(2−5)(2−6)(2−7))) +f(3)(((x−1)(x−2)(x−4)(x−5)(x−6)(x−7))/((3−1)(3−2)(3−4)(3−5)(3−6)(3−7))) +f(4)(((x−1)(x−2)(x−3)(x−5)(x−6)(x−7))/((4−1)(4−2)(4−3)(4−5)(4−6)(4−7))) +f(5)(((x−1)(x−2)(x−3)(x−4)(x−6)(x−7))/((5−1)(5−2)(5−3)(5−4)(5−6)(5−7))) +f(6)(((x−1)(x−2)(x−3)(x−4)(x−5)(x−7))/((6−1)(6−2)(6−3)(6−4)(6−5)(6−7))) +f(7)(((x−1)(x−2)(x−3)(x−4)(x−5)(x−6))/((7−1)(7−2)(7−3)(7−4)(7−5)(7−6))) x =f(8) =1×((6×5×4×3×2×1)/((−1)(−2)(−3)(−4)(−5)(−6))) +3×((7×5×4×3×2×1)/(1×(−1)(−2)(−3)(−4)(−5))) +7×((7×6×4×3×2×1)/(2×1×(−1)(−2)(−3)(−4))) +15×((7×6×5×3×2×1)/(3×2×1×(−1)(−2)(−3))) +30×((7×6×5×4×2×1)/(4×3×2×1×(−1)(−2))) +57×((7×6×5×4×3×1)/(5×4×3×2×1×(−1))) +103×((7×6×5×4×3×2)/(6×5×4×3×2×1)) =1−21+147−525+1050−1197+721 =176
$${f}\left(\mathrm{1}\right)=\mathrm{1},{f}\left(\mathrm{2}\right)=\mathrm{3},{f}\left(\mathrm{3}\right)=\mathrm{7},{f}\left(\mathrm{4}\right)=\mathrm{15} \\ $$$${f}\left(\mathrm{5}\right)=\mathrm{30},{f}\left(\mathrm{6}\right)=\mathrm{57},{f}\left(\mathrm{7}\right)=\mathrm{103},{f}\left(\mathrm{8}\right)={x} \\ $$$${f}\left({x}\right) \\ $$$$={f}\left(\mathrm{1}\right)\frac{\left({x}−\mathrm{2}\right)\left({x}−\mathrm{3}\right)\left({x}−\mathrm{4}\right)\left({x}−\mathrm{5}\right)\left({x}−\mathrm{6}\right)\left({x}−\mathrm{7}\right)}{\left(\mathrm{1}−\mathrm{2}\right)\left(\mathrm{1}−\mathrm{3}\right)\left(\mathrm{1}−\mathrm{4}\right)\left(\mathrm{1}−\mathrm{5}\right)\left(\mathrm{1}−\mathrm{6}\right)\left(\mathrm{1}−\mathrm{7}\right)} \\ $$$$+{f}\left(\mathrm{2}\right)\frac{\left({x}−\mathrm{1}\right)\left({x}−\mathrm{3}\right)\left({x}−\mathrm{4}\right)\left({x}−\mathrm{5}\right)\left({x}−\mathrm{6}\right)\left({x}−\mathrm{7}\right)}{\left(\mathrm{2}−\mathrm{1}\right)\left(\mathrm{2}−\mathrm{3}\right)\left(\mathrm{2}−\mathrm{4}\right)\left(\mathrm{2}−\mathrm{5}\right)\left(\mathrm{2}−\mathrm{6}\right)\left(\mathrm{2}−\mathrm{7}\right)} \\ $$$$+{f}\left(\mathrm{3}\right)\frac{\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)\left({x}−\mathrm{4}\right)\left({x}−\mathrm{5}\right)\left({x}−\mathrm{6}\right)\left({x}−\mathrm{7}\right)}{\left(\mathrm{3}−\mathrm{1}\right)\left(\mathrm{3}−\mathrm{2}\right)\left(\mathrm{3}−\mathrm{4}\right)\left(\mathrm{3}−\mathrm{5}\right)\left(\mathrm{3}−\mathrm{6}\right)\left(\mathrm{3}−\mathrm{7}\right)} \\ $$$$+{f}\left(\mathrm{4}\right)\frac{\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)\left({x}−\mathrm{3}\right)\left({x}−\mathrm{5}\right)\left({x}−\mathrm{6}\right)\left({x}−\mathrm{7}\right)}{\left(\mathrm{4}−\mathrm{1}\right)\left(\mathrm{4}−\mathrm{2}\right)\left(\mathrm{4}−\mathrm{3}\right)\left(\mathrm{4}−\mathrm{5}\right)\left(\mathrm{4}−\mathrm{6}\right)\left(\mathrm{4}−\mathrm{7}\right)} \\ $$$$+{f}\left(\mathrm{5}\right)\frac{\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)\left({x}−\mathrm{3}\right)\left({x}−\mathrm{4}\right)\left({x}−\mathrm{6}\right)\left({x}−\mathrm{7}\right)}{\left(\mathrm{5}−\mathrm{1}\right)\left(\mathrm{5}−\mathrm{2}\right)\left(\mathrm{5}−\mathrm{3}\right)\left(\mathrm{5}−\mathrm{4}\right)\left(\mathrm{5}−\mathrm{6}\right)\left(\mathrm{5}−\mathrm{7}\right)} \\ $$$$+{f}\left(\mathrm{6}\right)\frac{\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)\left({x}−\mathrm{3}\right)\left({x}−\mathrm{4}\right)\left({x}−\mathrm{5}\right)\left({x}−\mathrm{7}\right)}{\left(\mathrm{6}−\mathrm{1}\right)\left(\mathrm{6}−\mathrm{2}\right)\left(\mathrm{6}−\mathrm{3}\right)\left(\mathrm{6}−\mathrm{4}\right)\left(\mathrm{6}−\mathrm{5}\right)\left(\mathrm{6}−\mathrm{7}\right)} \\ $$$$+{f}\left(\mathrm{7}\right)\frac{\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)\left({x}−\mathrm{3}\right)\left({x}−\mathrm{4}\right)\left({x}−\mathrm{5}\right)\left({x}−\mathrm{6}\right)}{\left(\mathrm{7}−\mathrm{1}\right)\left(\mathrm{7}−\mathrm{2}\right)\left(\mathrm{7}−\mathrm{3}\right)\left(\mathrm{7}−\mathrm{4}\right)\left(\mathrm{7}−\mathrm{5}\right)\left(\mathrm{7}−\mathrm{6}\right)} \\ $$$${x} \\ $$$$={f}\left(\mathrm{8}\right) \\ $$$$=\mathrm{1}×\frac{\mathrm{6}×\mathrm{5}×\mathrm{4}×\mathrm{3}×\mathrm{2}×\mathrm{1}}{\left(−\mathrm{1}\right)\left(−\mathrm{2}\right)\left(−\mathrm{3}\right)\left(−\mathrm{4}\right)\left(−\mathrm{5}\right)\left(−\mathrm{6}\right)} \\ $$$$+\mathrm{3}×\frac{\mathrm{7}×\mathrm{5}×\mathrm{4}×\mathrm{3}×\mathrm{2}×\mathrm{1}}{\mathrm{1}×\left(−\mathrm{1}\right)\left(−\mathrm{2}\right)\left(−\mathrm{3}\right)\left(−\mathrm{4}\right)\left(−\mathrm{5}\right)} \\ $$$$+\mathrm{7}×\frac{\mathrm{7}×\mathrm{6}×\mathrm{4}×\mathrm{3}×\mathrm{2}×\mathrm{1}}{\mathrm{2}×\mathrm{1}×\left(−\mathrm{1}\right)\left(−\mathrm{2}\right)\left(−\mathrm{3}\right)\left(−\mathrm{4}\right)} \\ $$$$+\mathrm{15}×\frac{\mathrm{7}×\mathrm{6}×\mathrm{5}×\mathrm{3}×\mathrm{2}×\mathrm{1}}{\mathrm{3}×\mathrm{2}×\mathrm{1}×\left(−\mathrm{1}\right)\left(−\mathrm{2}\right)\left(−\mathrm{3}\right)} \\ $$$$+\mathrm{30}×\frac{\mathrm{7}×\mathrm{6}×\mathrm{5}×\mathrm{4}×\mathrm{2}×\mathrm{1}}{\mathrm{4}×\mathrm{3}×\mathrm{2}×\mathrm{1}×\left(−\mathrm{1}\right)\left(−\mathrm{2}\right)} \\ $$$$+\mathrm{57}×\frac{\mathrm{7}×\mathrm{6}×\mathrm{5}×\mathrm{4}×\mathrm{3}×\mathrm{1}}{\mathrm{5}×\mathrm{4}×\mathrm{3}×\mathrm{2}×\mathrm{1}×\left(−\mathrm{1}\right)} \\ $$$$+\mathrm{103}×\frac{\mathrm{7}×\mathrm{6}×\mathrm{5}×\mathrm{4}×\mathrm{3}×\mathrm{2}}{\mathrm{6}×\mathrm{5}×\mathrm{4}×\mathrm{3}×\mathrm{2}×\mathrm{1}} \\ $$$$=\mathrm{1}−\mathrm{21}+\mathrm{147}−\mathrm{525}+\mathrm{1050}−\mathrm{1197}+\mathrm{721} \\ $$$$=\mathrm{176} \\ $$
Commented by MJS last updated on 23/Jul/19
generally it could be any number. we′re interpreting it as y=c_6 x^6 +c_5 x^5 +c_4 x^4 +c_3 x^3 +c_2 x^2 +c_1 x+c_0 with given pairs (x, y): (1, 1) (2, 3) (3, 7) (4, 15) (5, 30) (6, 57) (7, 103) but we can use any function with 7 unknown constants y=(1/(c_6 x^6 +c_5 x^5 +c_4 x^4 +c_3 x^3 +c_2 x^2 +c_1 x+c_0 )) leads to ((3914)/(781)) y=(c_6 /x^6 )+(c_5 /x^5 )+(c_4 /x^4 )+(c_3 /x^3 )+(c_2 /x^2 )+(c_1 /x)+c_0 leads to ((43339367)/(262144)) y=(1/((c_6 /x^6 )+(c_5 /x^5 )+(c_4 /x^4 )+(c_3 /x^3 )+(c_2 /x^2 )+(c_1 /x)+c_0 )) leads to ((1026031616)/(5937579)) we could also use y=c_7 x^7 +c_6 x^6 +c_5 x^5 +c_4 x^4 +c_3 x^3 +c_2 x^2 +c_1 x+c_0 then we have one factor free to choose: y=−((c_0 +2)/(5040))x^7 +((4c_0 +7)/(720))x^6 −((46c_0 +65)/(720))x^5 +((56c_0 +65)/(144))x^4 −((967c_0 +749)/(720))x^3 +((469c_0 +277)/(180))x^2 −((11(99c_0 −5))/(420))x+c_0 x=8 y=174−c_0 ⇒ any value fits
$$\mathrm{generally}\:\mathrm{it}\:\mathrm{could}\:\mathrm{be}\:\mathrm{any}\:\mathrm{number}. \\ $$$$\mathrm{we}'\mathrm{re}\:\mathrm{interpreting}\:\mathrm{it}\:\mathrm{as} \\ $$$${y}={c}_{\mathrm{6}} {x}^{\mathrm{6}} +{c}_{\mathrm{5}} {x}^{\mathrm{5}} +{c}_{\mathrm{4}} {x}^{\mathrm{4}} +{c}_{\mathrm{3}} {x}^{\mathrm{3}} +{c}_{\mathrm{2}} {x}^{\mathrm{2}} +{c}_{\mathrm{1}} {x}+{c}_{\mathrm{0}} \\ $$$$\mathrm{with}\:\mathrm{given}\:\mathrm{pairs}\:\left({x},\:{y}\right): \\ $$$$\left(\mathrm{1},\:\mathrm{1}\right)\:\:\left(\mathrm{2},\:\mathrm{3}\right)\:\:\left(\mathrm{3},\:\mathrm{7}\right)\:\:\left(\mathrm{4},\:\mathrm{15}\right)\:\:\left(\mathrm{5},\:\mathrm{30}\right)\:\:\left(\mathrm{6},\:\mathrm{57}\right)\:\:\left(\mathrm{7},\:\mathrm{103}\right) \\ $$$$ \\ $$$$\mathrm{but}\:\mathrm{we}\:\mathrm{can}\:\mathrm{use}\:\mathrm{any}\:\mathrm{function}\:\mathrm{with}\:\mathrm{7}\:\mathrm{unknown} \\ $$$$\mathrm{constants} \\ $$$${y}=\frac{\mathrm{1}}{{c}_{\mathrm{6}} {x}^{\mathrm{6}} +{c}_{\mathrm{5}} {x}^{\mathrm{5}} +{c}_{\mathrm{4}} {x}^{\mathrm{4}} +{c}_{\mathrm{3}} {x}^{\mathrm{3}} +{c}_{\mathrm{2}} {x}^{\mathrm{2}} +{c}_{\mathrm{1}} {x}+{c}_{\mathrm{0}} } \\ $$$$\mathrm{leads}\:\mathrm{to}\:\frac{\mathrm{3914}}{\mathrm{781}} \\ $$$${y}=\frac{{c}_{\mathrm{6}} }{{x}^{\mathrm{6}} }+\frac{{c}_{\mathrm{5}} }{{x}^{\mathrm{5}} }+\frac{{c}_{\mathrm{4}} }{{x}^{\mathrm{4}} }+\frac{{c}_{\mathrm{3}} }{{x}^{\mathrm{3}} }+\frac{{c}_{\mathrm{2}} }{{x}^{\mathrm{2}} }+\frac{{c}_{\mathrm{1}} }{{x}}+{c}_{\mathrm{0}} \\ $$$$\mathrm{leads}\:\mathrm{to}\:\frac{\mathrm{43339367}}{\mathrm{262144}} \\ $$$${y}=\frac{\mathrm{1}}{\frac{{c}_{\mathrm{6}} }{{x}^{\mathrm{6}} }+\frac{{c}_{\mathrm{5}} }{{x}^{\mathrm{5}} }+\frac{{c}_{\mathrm{4}} }{{x}^{\mathrm{4}} }+\frac{{c}_{\mathrm{3}} }{{x}^{\mathrm{3}} }+\frac{{c}_{\mathrm{2}} }{{x}^{\mathrm{2}} }+\frac{{c}_{\mathrm{1}} }{{x}}+{c}_{\mathrm{0}} } \\ $$$$\mathrm{leads}\:\mathrm{to}\:\frac{\mathrm{1026031616}}{\mathrm{5937579}} \\ $$$$\mathrm{we}\:\mathrm{could}\:\mathrm{also}\:\mathrm{use} \\ $$$${y}={c}_{\mathrm{7}} {x}^{\mathrm{7}} +{c}_{\mathrm{6}} {x}^{\mathrm{6}} +{c}_{\mathrm{5}} {x}^{\mathrm{5}} +{c}_{\mathrm{4}} {x}^{\mathrm{4}} +{c}_{\mathrm{3}} {x}^{\mathrm{3}} +{c}_{\mathrm{2}} {x}^{\mathrm{2}} +{c}_{\mathrm{1}} {x}+{c}_{\mathrm{0}} \\ $$$$\mathrm{then}\:\mathrm{we}\:\mathrm{have}\:\mathrm{one}\:\mathrm{factor}\:\mathrm{free}\:\mathrm{to}\:\mathrm{choose}: \\ $$$${y}=−\frac{{c}_{\mathrm{0}} +\mathrm{2}}{\mathrm{5040}}{x}^{\mathrm{7}} +\frac{\mathrm{4}{c}_{\mathrm{0}} +\mathrm{7}}{\mathrm{720}}{x}^{\mathrm{6}} −\frac{\mathrm{46}{c}_{\mathrm{0}} +\mathrm{65}}{\mathrm{720}}{x}^{\mathrm{5}} +\frac{\mathrm{56}{c}_{\mathrm{0}} +\mathrm{65}}{\mathrm{144}}{x}^{\mathrm{4}} −\frac{\mathrm{967}{c}_{\mathrm{0}} +\mathrm{749}}{\mathrm{720}}{x}^{\mathrm{3}} +\frac{\mathrm{469}{c}_{\mathrm{0}} +\mathrm{277}}{\mathrm{180}}{x}^{\mathrm{2}} −\frac{\mathrm{11}\left(\mathrm{99}{c}_{\mathrm{0}} −\mathrm{5}\right)}{\mathrm{420}}{x}+{c}_{\mathrm{0}} \\ $$$${x}=\mathrm{8} \\ $$$${y}=\mathrm{174}−{c}_{\mathrm{0}} \\ $$$$\Rightarrow\:\mathrm{any}\:\mathrm{value}\:\mathrm{fits} \\ $$
Answered by MJS last updated on 23/Jul/19
1 3 7 15 30 57 103 176 2 4 8 15 27 46 73 2 4 7 12 19 27 2 3 5 7 8 1 2 2 1 1 0 −1 −1 −1
$$\mathrm{1}\:\:\:\mathrm{3}\:\:\:\mathrm{7}\:\:\mathrm{15}\:\:\mathrm{30}\:\:\mathrm{57}\:\mathrm{103}\:\:\:\mathrm{176} \\ $$$$\:\:\mathrm{2}\:\:\:\mathrm{4}\:\:\:\mathrm{8}\:\:\mathrm{15}\:\:\mathrm{27}\:\:\:\mathrm{46}\:\:\:\:\mathrm{73} \\ $$$$\:\:\:\:\:\mathrm{2}\:\:\:\mathrm{4}\:\:\:\mathrm{7}\:\:\mathrm{12}\:\:\:\mathrm{19}\:\:\:\:\mathrm{27} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{2}\:\:\:\mathrm{3}\:\:\:\mathrm{5}\:\:\:\:\mathrm{7}\:\:\:\:\:\:\mathrm{8} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\mathrm{2}\:\:\:\mathrm{2}\:\:\:\:\:\:\:\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\mathrm{0}\:\:\:−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{1}\:−\mathrm{1} \\ $$
Commented by Tony Lin last updated on 23/Jul/19
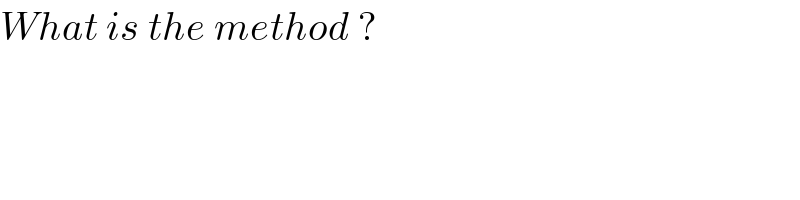
What is the method ?
$${What}\:{is}\:{the}\:{method}\:? \\ $$
Commented by MJS last updated on 23/Jul/19
a b c d... b−a c−b d−c... (c−b)−(b−a) (d−c)−(c−b)... ... until you reach a line with each number of the same value. then start at the bottom adding this number once more and go up from line to line. this gives the same result as the polynomial approach we can say the 1^(st) line is y the 2^(nd) line is △y the 3^(rd) line is △^2 y the n^(th) line is △^(n−1) y it′s similar to the n^(th) derivate of a polynome of degree k. you reach the constant factor after k steps
$${a}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{b}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{c}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{d}… \\ $$$$\:\:{b}−{a}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{c}−{b}\:\:\:\:\:\:\:\:\:\:\:\:\:\:{d}−{c}… \\ $$$$\:\:\:\:\:\:\:\:\:\:\left({c}−{b}\right)−\left({b}−{a}\right)\:\:\:\:\:\:\:\:\:\:\:\left({d}−{c}\right)−\left({c}−{b}\right)… \\ $$$$… \\ $$$$\mathrm{until}\:\mathrm{you}\:\mathrm{reach}\:\mathrm{a}\:\mathrm{line}\:\mathrm{with}\:\mathrm{each}\:\mathrm{number}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{same}\:\mathrm{value}.\:\mathrm{then}\:\mathrm{start}\:\mathrm{at}\:\mathrm{the}\:\mathrm{bottom} \\ $$$$\mathrm{adding}\:\mathrm{this}\:\mathrm{number}\:\mathrm{once}\:\mathrm{more}\:\mathrm{and}\:\mathrm{go}\:\mathrm{up} \\ $$$$\mathrm{from}\:\mathrm{line}\:\mathrm{to}\:\mathrm{line}.\:\mathrm{this}\:\mathrm{gives}\:\mathrm{the}\:\mathrm{same}\:\mathrm{result} \\ $$$$\mathrm{as}\:\mathrm{the}\:\mathrm{polynomial}\:\mathrm{approach} \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{say} \\ $$$$\mathrm{the}\:\mathrm{1}^{\mathrm{st}} \:\mathrm{line}\:\mathrm{is}\:{y} \\ $$$$\mathrm{the}\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{line}\:\mathrm{is}\:\bigtriangleup{y} \\ $$$$\mathrm{the}\:\mathrm{3}^{\mathrm{rd}} \:\mathrm{line}\:\mathrm{is}\:\bigtriangleup^{\mathrm{2}} {y} \\ $$$$\mathrm{the}\:{n}^{\mathrm{th}} \:\mathrm{line}\:\mathrm{is}\:\bigtriangleup^{{n}−\mathrm{1}} {y} \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{similar}\:\mathrm{to}\:\mathrm{the}\:{n}^{\mathrm{th}} \:\mathrm{derivate}\:\mathrm{of}\:\mathrm{a}\:\mathrm{polynome} \\ $$$$\mathrm{of}\:\mathrm{degree}\:{k}.\:\mathrm{you}\:\mathrm{reach}\:\mathrm{the}\:\mathrm{constant}\:\mathrm{factor} \\ $$$$\mathrm{after}\:{k}\:\mathrm{steps} \\ $$
Commented by Tony Lin last updated on 23/Jul/19
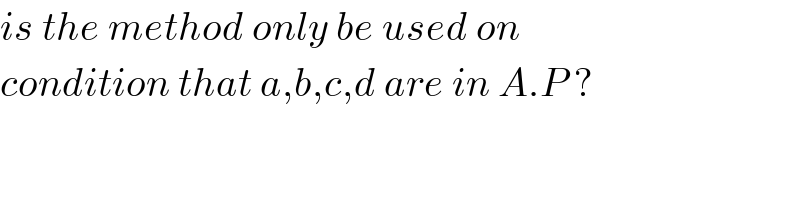
is the method only be used on condition that a,b,c,d are in A.P ?
$${is}\:{the}\:{method}\:{only}\:{be}\:{used}\:{on}\: \\ $$$${condition}\:{that}\:{a},{b},{c},{d}\:{are}\:{in}\:{A}.{P}\:? \\ $$
Commented by MJS last updated on 23/Jul/19
no. write down any numbers, it always works but you′ll only find polynomial solutions 1 1 2 3 5 8 13 29 0 1 1 2 3 5 16 1 0 1 1 2 11 −1 1 0 1 9 2 −1 1 8 −3 2 7 5 5
$$\mathrm{no}.\:\mathrm{write}\:\mathrm{down}\:\mathrm{any}\:\mathrm{numbers},\:\mathrm{it}\:\mathrm{always}\:\mathrm{works} \\ $$$$\mathrm{but}\:\mathrm{you}'\mathrm{ll}\:\mathrm{only}\:\mathrm{find}\:\mathrm{polynomial}\:\mathrm{solutions} \\ $$$$\mathrm{1}\:\:\:\:\:\mathrm{1}\:\:\:\:\:\mathrm{2}\:\:\:\:\:\mathrm{3}\:\:\:\:\:\mathrm{5}\:\:\:\:\:\mathrm{8}\:\:\:\:\:\mathrm{13}\:\:\:\:\:\mathrm{29} \\ $$$$\:\:\:\:\mathrm{0}\:\:\:\:\:\mathrm{1}\:\:\:\:\:\mathrm{1}\:\:\:\:\:\mathrm{2}\:\:\:\:\:\mathrm{3}\:\:\:\:\:\mathrm{5}\:\:\:\:\:\mathrm{16} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\mathrm{0}\:\:\:\:\:\mathrm{1}\:\:\:\:\:\mathrm{1}\:\:\:\:\:\mathrm{2}\:\:\:\:\:\mathrm{11} \\ $$$$\:\:\:\:\:\:\:\:\:\:−\mathrm{1}\:\:\:\mathrm{1}\:\:\:\:\:\mathrm{0}\:\:\:\:\:\mathrm{1}\:\:\:\:\:\mathrm{9} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}\:\:−\mathrm{1}\:\:\:\:\mathrm{1}\:\:\:\:\mathrm{8} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{3}\:\:\:\mathrm{2}\:\:\:\:\:\mathrm{7} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{5}\:\:\:\:\:\mathrm{5} \\ $$
Commented by Tony Lin last updated on 23/Jul/19
thanks sir .i got it.
$${thanks}\:{sir}\:.{i}\:{got}\:{it}. \\ $$
Commented by MJS last updated on 23/Jul/19
you′re welcome
$$\mathrm{you}'\mathrm{re}\:\mathrm{welcome} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *