Question Number 120551 by bobhans last updated on 01/Nov/20
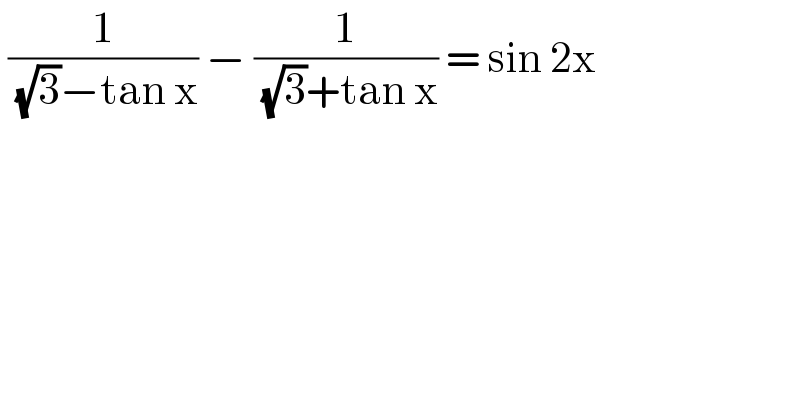
$$\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}−\mathrm{tan}\:\mathrm{x}}\:−\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}+\mathrm{tan}\:\mathrm{x}}\:=\:\mathrm{sin}\:\mathrm{2x} \\ $$
Answered by john santu last updated on 01/Nov/20

$${recall}\:{that}\:\mathrm{sin}\:\mathrm{2}{x}\:=\:\frac{\mathrm{2tan}\:{x}}{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} {x}} \\ $$$$\Leftrightarrow\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}−\mathrm{tan}\:{x}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}+\mathrm{tan}\:{x}}\:=\:\frac{\mathrm{2tan}\:{x}}{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} {x}} \\ $$$${letting}\:\mathrm{tan}\:{x}\:=\:{p}\:,\:{gives}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}−{p}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}+{p}}=\frac{\mathrm{2}{p}}{\mathrm{1}+{p}^{\mathrm{2}} } \\ $$$$\Leftrightarrow\:\frac{\mathrm{2}{p}}{\mathrm{3}−{p}^{\mathrm{2}} }\:=\:\frac{\mathrm{2}{p}}{\mathrm{1}+{p}^{\mathrm{2}} }\:;\:\frac{\mathrm{2}{p}\left(\mathrm{1}+{p}^{\mathrm{2}} −\mathrm{3}+{p}^{\mathrm{2}} \right)}{\left(\mathrm{3}−{p}^{\mathrm{2}} \right)\left(\mathrm{1}+{p}^{\mathrm{2}} \right)}=\mathrm{0} \\ $$$$\rightarrow\:\mathrm{2}{p}\:\left(\mathrm{2}{p}^{\mathrm{2}} −\mathrm{2}\right)=\mathrm{0}\:\rightarrow\begin{cases}{{p}=\mathrm{0}\Rightarrow\mathrm{tan}\:{x}=\mathrm{0}\:;\:{x}={n}\pi}\\{{p}=\pm\mathrm{1}\Rightarrow\mathrm{tan}\:{x}=\pm\mathrm{1};{x}=\pm\frac{\pi}{\mathrm{4}}+{n}\pi}\end{cases} \\ $$
