Question Number 89487 by cindiaulia last updated on 17/Apr/20
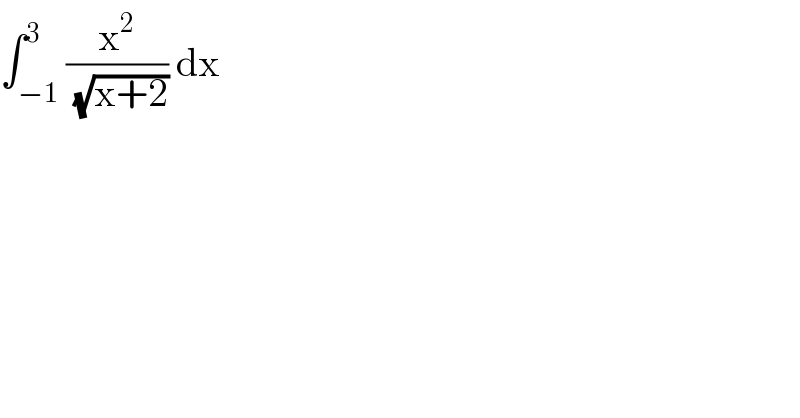
$$\int_{−\mathrm{1}} ^{\mathrm{3}} \frac{\mathrm{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{x}+\mathrm{2}}}\:\mathrm{dx} \\ $$
Commented by niroj last updated on 17/Apr/20
![∫_(−1) ^( 3) (( x^2 )/( (√(x+2))))dx put (√(x+2))=t x+2= t^2 , x^2 =(t^2 −2)^2 dx=2tdt If x=3 ⇒ t=(√5) Ifx=−1⇒ t=1 ∫_1 ^( (√5)) (((t^2 −2)^2 )/t).2tdt =2 ∫_1 ^( (√5)) (t^4 −4t^2 +4)dt = [2 ((t^5 /5)−((4t^3 )/3)+4t)]_1 ^(√5) =2 [ (((((√5))^5 )/5)−((4((√5) )^3 )/3)+4(√5) )−((1/5)−(4/3)+4)] = 2[( ((25(√5))/5)−((20(√5))/3)+(√5) )−(4+((3−20)/(15)))] = 2[ ((√5) +((75(√5) −100(√5))/(15)))−(((60−17)/(15)))] = 2[ ((( 15(√5) −25(√5))/(15)))−((43)/(15))] = 2(((−10(√5))/(15))−((43)/(15))) = −2(((10(√5) +43)/(15)))//.](https://www.tinkutara.com/question/Q89499.png)
$$\:\int_{−\mathrm{1}} ^{\:\mathrm{3}} \:\frac{\:\mathrm{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{x}+\mathrm{2}}}\mathrm{dx}\: \\ $$$$\:\:\mathrm{put}\:\:\sqrt{\mathrm{x}+\mathrm{2}}=\mathrm{t} \\ $$$$\:\:\:\mathrm{x}+\mathrm{2}=\:\mathrm{t}^{\mathrm{2}} \:,\:\:\mathrm{x}^{\mathrm{2}} =\left(\mathrm{t}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\mathrm{dx}=\mathrm{2tdt} \\ $$$$\:\mathrm{If}\:\mathrm{x}=\mathrm{3}\:\Rightarrow\:\mathrm{t}=\sqrt{\mathrm{5}} \\ $$$$\:\mathrm{Ifx}=−\mathrm{1}\Rightarrow\:\mathrm{t}=\mathrm{1} \\ $$$$\:\:\:\:\int_{\mathrm{1}} ^{\:\sqrt{\mathrm{5}}} \:\:\frac{\left(\mathrm{t}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} }{\mathrm{t}}.\mathrm{2tdt} \\ $$$$\:=\mathrm{2}\:\int_{\mathrm{1}} ^{\:\sqrt{\mathrm{5}}} \:\left(\mathrm{t}^{\mathrm{4}} −\mathrm{4t}^{\mathrm{2}} +\mathrm{4}\right)\mathrm{dt} \\ $$$$\:\:=\:\left[\mathrm{2}\:\left(\frac{\mathrm{t}^{\mathrm{5}} }{\mathrm{5}}−\frac{\mathrm{4t}^{\mathrm{3}} }{\mathrm{3}}+\mathrm{4t}\right)\right]_{\mathrm{1}} ^{\sqrt{\mathrm{5}}} \\ $$$$=\mathrm{2}\:\left[\:\left(\frac{\left(\sqrt{\mathrm{5}}\right)^{\mathrm{5}} }{\mathrm{5}}−\frac{\mathrm{4}\left(\sqrt{\mathrm{5}}\:\right)^{\mathrm{3}} }{\mathrm{3}}+\mathrm{4}\sqrt{\mathrm{5}}\:\right)−\left(\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{4}}{\mathrm{3}}+\mathrm{4}\right)\right] \\ $$$$=\:\:\mathrm{2}\left[\left(\:\frac{\mathrm{25}\sqrt{\mathrm{5}}}{\mathrm{5}}−\frac{\mathrm{20}\sqrt{\mathrm{5}}}{\mathrm{3}}+\sqrt{\mathrm{5}}\:\right)−\left(\mathrm{4}+\frac{\mathrm{3}−\mathrm{20}}{\mathrm{15}}\right)\right] \\ $$$$=\:\mathrm{2}\left[\:\left(\sqrt{\mathrm{5}}\:+\frac{\mathrm{75}\sqrt{\mathrm{5}}\:−\mathrm{100}\sqrt{\mathrm{5}}}{\mathrm{15}}\right)−\left(\frac{\mathrm{60}−\mathrm{17}}{\mathrm{15}}\right)\right] \\ $$$$=\:\mathrm{2}\left[\:\left(\frac{\:\mathrm{15}\sqrt{\mathrm{5}}\:\:−\mathrm{25}\sqrt{\mathrm{5}}}{\mathrm{15}}\right)−\frac{\mathrm{43}}{\mathrm{15}}\right] \\ $$$$=\:\mathrm{2}\left(\frac{−\mathrm{10}\sqrt{\mathrm{5}}}{\mathrm{15}}−\frac{\mathrm{43}}{\mathrm{15}}\right) \\ $$$$=\:−\mathrm{2}\left(\frac{\mathrm{10}\sqrt{\mathrm{5}}\:\:+\mathrm{43}}{\mathrm{15}}\right)//. \\ $$$$ \\ $$$$ \\ $$
