Question Number 125962 by bramlexs22 last updated on 15/Dec/20
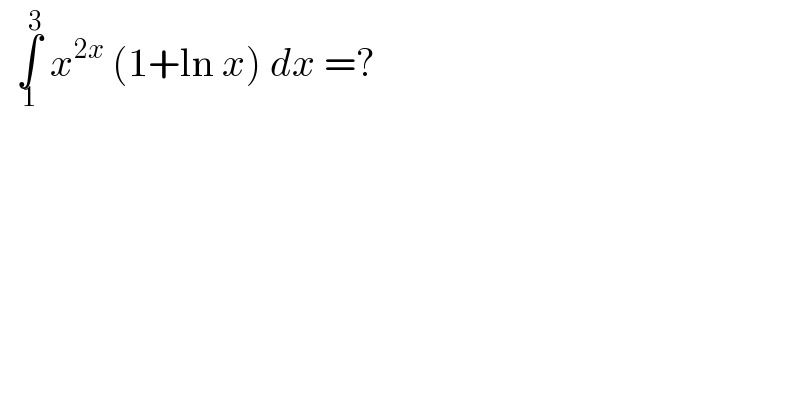
$$\:\:\underset{\mathrm{1}} {\overset{\mathrm{3}} {\int}}\:{x}^{\mathrm{2}{x}} \:\left(\mathrm{1}+\mathrm{ln}\:{x}\right)\:{dx}\:=?\: \\ $$
Answered by liberty last updated on 16/Dec/20
![let x^x = r → { ((x=1→r=1)),((x=3→r=27)) :} ∧ dr = x^x (1+ln x)dx I=∫_1 ^3 x^x .x^x (1+ln x) dx = ∫_1 ^(27) r dr I= (1/2)[ r^2 ]_1 ^(27) = (1/2)×28×26 = 14×26= 364](https://www.tinkutara.com/question/Q125963.png)
$$\:{let}\:{x}^{{x}} \:=\:{r}\:\rightarrow\begin{cases}{{x}=\mathrm{1}\rightarrow{r}=\mathrm{1}}\\{{x}=\mathrm{3}\rightarrow{r}=\mathrm{27}}\end{cases}\:\wedge\:{dr}\:=\:{x}^{{x}} \left(\mathrm{1}+\mathrm{ln}\:{x}\right){dx} \\ $$$${I}=\underset{\mathrm{1}} {\overset{\mathrm{3}} {\int}}\:{x}^{{x}} \:.{x}^{{x}} \left(\mathrm{1}+\mathrm{ln}\:{x}\right)\:{dx}\:=\:\underset{\mathrm{1}} {\overset{\mathrm{27}} {\int}}\:{r}\:{dr}\: \\ $$$${I}=\:\frac{\mathrm{1}}{\mathrm{2}}\left[\:{r}^{\mathrm{2}} \:\right]_{\mathrm{1}} ^{\mathrm{27}} \:=\:\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{28}×\mathrm{26}\:=\:\mathrm{14}×\mathrm{26}=\:\mathrm{364} \\ $$$$ \\ $$
