Question Number 129788 by bramlexs22 last updated on 19/Jan/21
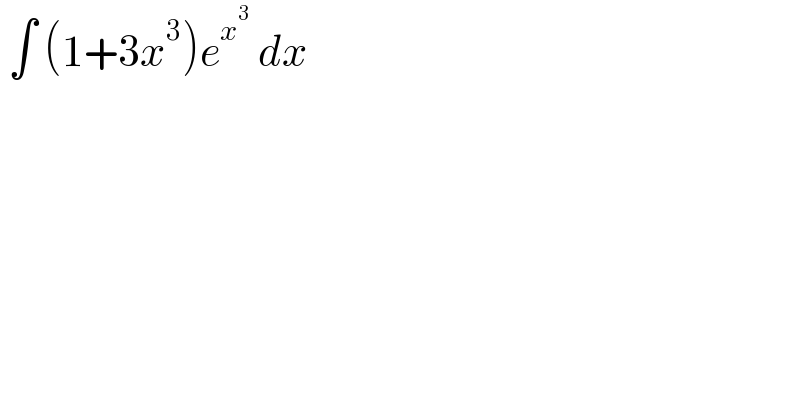
$$\:\int\:\left(\mathrm{1}+\mathrm{3}{x}^{\mathrm{3}} \right){e}^{{x}^{\mathrm{3}} } \:{dx}\: \\ $$
Answered by EDWIN88 last updated on 19/Jan/21
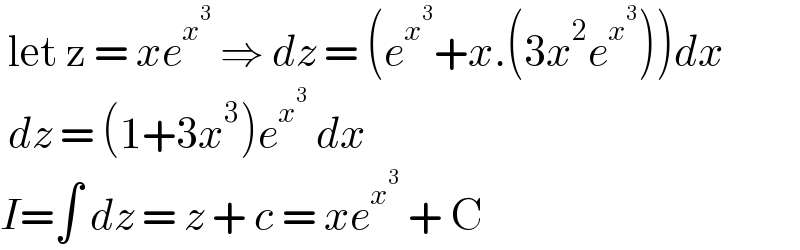
$$\:\mathrm{let}\:\mathrm{z}\:=\:{xe}^{{x}^{\mathrm{3}} } \:\Rightarrow\:{dz}\:=\:\left({e}^{{x}^{\mathrm{3}} } +{x}.\left(\mathrm{3}{x}^{\mathrm{2}} {e}^{{x}^{\mathrm{3}} } \right)\right){dx} \\ $$$$\:{dz}\:=\:\left(\mathrm{1}+\mathrm{3}{x}^{\mathrm{3}} \right){e}^{{x}^{\mathrm{3}} } \:{dx} \\ $$$${I}=\int\:{dz}\:=\:{z}\:+\:{c}\:=\:{xe}^{{x}^{\mathrm{3}} } \:+\:\mathrm{C}\: \\ $$
