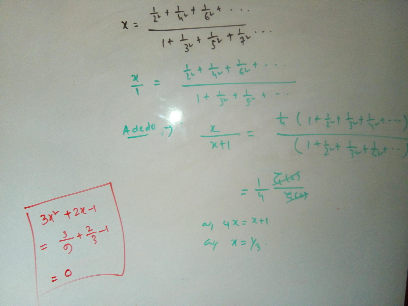Question Number 55094 by naka3546 last updated on 17/Feb/19
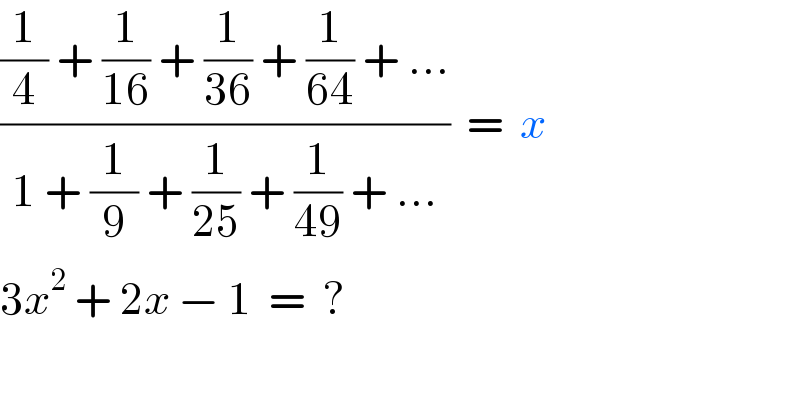
$$\frac{\frac{\mathrm{1}}{\mathrm{4}}\:+\:\frac{\mathrm{1}}{\mathrm{16}}\:+\:\frac{\mathrm{1}}{\mathrm{36}}\:+\:\frac{\mathrm{1}}{\mathrm{64}}\:+\:…}{\mathrm{1}\:+\:\frac{\mathrm{1}}{\mathrm{9}}\:+\:\frac{\mathrm{1}}{\mathrm{25}}\:+\:\frac{\mathrm{1}}{\mathrm{49}}\:+\:…}\:\:=\:\:{x} \\ $$$$\mathrm{3}{x}^{\mathrm{2}} \:+\:\mathrm{2}{x}\:−\:\mathrm{1}\:\:=\:\:? \\ $$
Commented by maxmathsup by imad last updated on 17/Feb/19
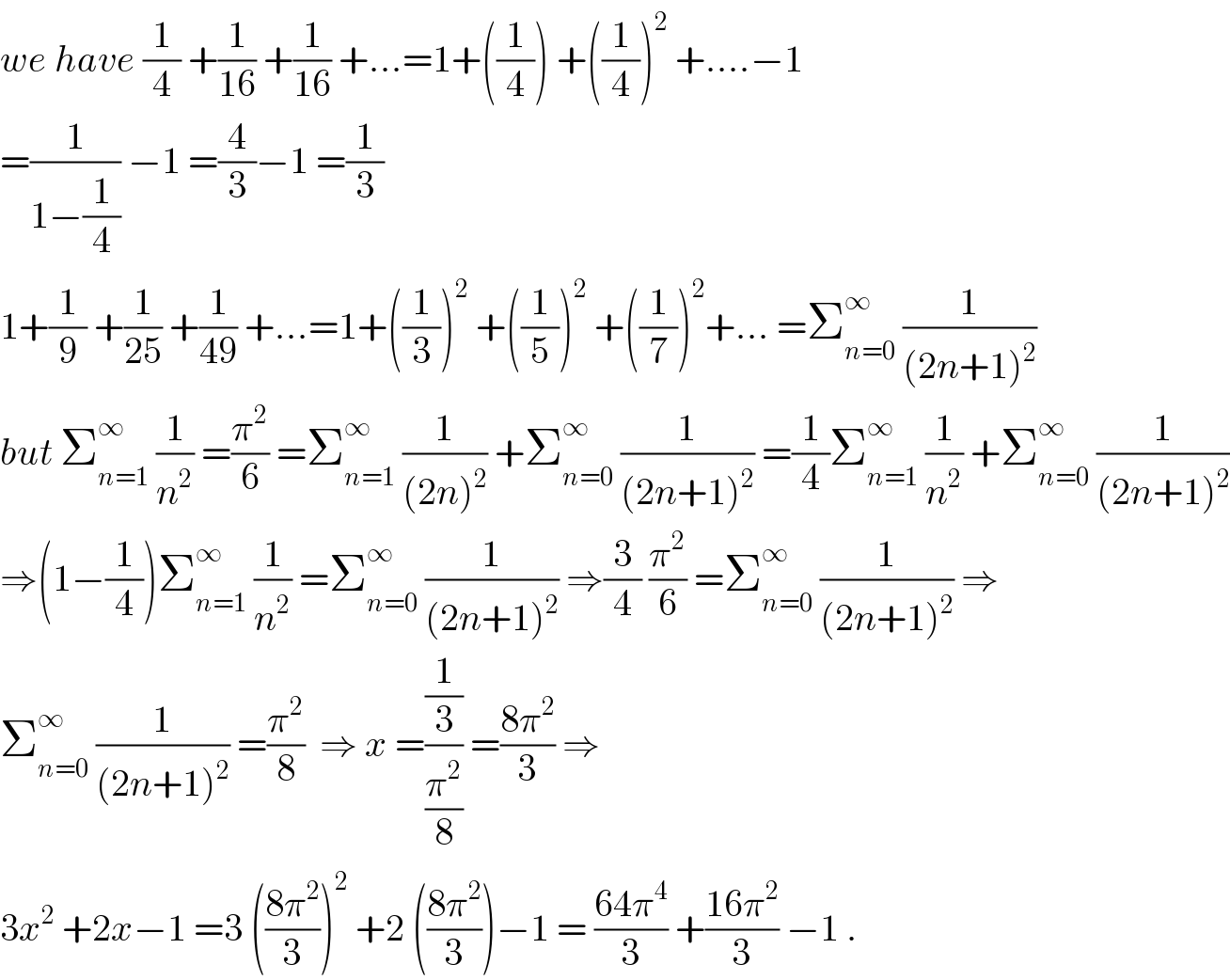
$${we}\:{have}\:\frac{\mathrm{1}}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{16}}\:+\frac{\mathrm{1}}{\mathrm{16}}\:+…=\mathrm{1}+\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\:+\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} \:+….−\mathrm{1} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}}\:−\mathrm{1}\:=\frac{\mathrm{4}}{\mathrm{3}}−\mathrm{1}\:=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{1}+\frac{\mathrm{1}}{\mathrm{9}}\:+\frac{\mathrm{1}}{\mathrm{25}}\:+\frac{\mathrm{1}}{\mathrm{49}}\:+…=\mathrm{1}+\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} \:+\left(\frac{\mathrm{1}}{\mathrm{5}}\right)^{\mathrm{2}} \:+\left(\frac{\mathrm{1}}{\mathrm{7}}\right)^{\mathrm{2}} +…\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${but}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}\right)^{\mathrm{2}} }\:+\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{4}}\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:+\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}\right)\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow\frac{\mathrm{3}}{\mathrm{4}}\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:\:\Rightarrow\:{x}\:=\frac{\frac{\mathrm{1}}{\mathrm{3}}}{\frac{\pi^{\mathrm{2}} }{\mathrm{8}}}\:=\frac{\mathrm{8}\pi^{\mathrm{2}} }{\mathrm{3}}\:\Rightarrow \\ $$$$\mathrm{3}{x}^{\mathrm{2}} \:+\mathrm{2}{x}−\mathrm{1}\:=\mathrm{3}\:\left(\frac{\mathrm{8}\pi^{\mathrm{2}} }{\mathrm{3}}\right)^{\mathrm{2}} \:+\mathrm{2}\:\left(\frac{\mathrm{8}\pi^{\mathrm{2}} }{\mathrm{3}}\right)−\mathrm{1}\:=\:\frac{\mathrm{64}\pi^{\mathrm{4}} }{\mathrm{3}}\:+\frac{\mathrm{16}\pi^{\mathrm{2}} }{\mathrm{3}}\:−\mathrm{1}\:. \\ $$
Commented by maxmathsup by imad last updated on 17/Feb/19
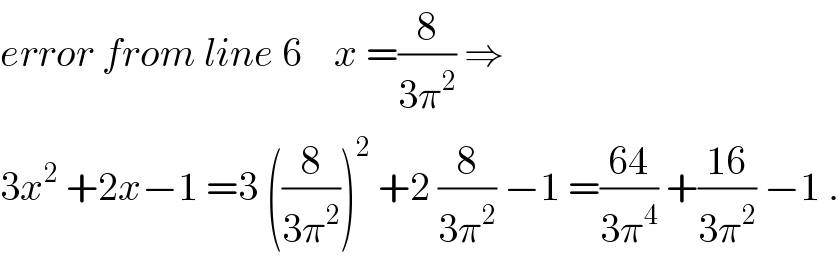
$${error}\:{from}\:{line}\:\mathrm{6}\:\:\:\:{x}\:=\frac{\mathrm{8}}{\mathrm{3}\pi^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{3}{x}^{\mathrm{2}} \:+\mathrm{2}{x}−\mathrm{1}\:=\mathrm{3}\:\left(\frac{\mathrm{8}}{\mathrm{3}\pi^{\mathrm{2}} }\right)^{\mathrm{2}} \:+\mathrm{2}\:\frac{\mathrm{8}}{\mathrm{3}\pi^{\mathrm{2}} }\:−\mathrm{1}\:=\frac{\mathrm{64}}{\mathrm{3}\pi^{\mathrm{4}} }\:+\frac{\mathrm{16}}{\mathrm{3}\pi^{\mathrm{2}} }\:−\mathrm{1}\:. \\ $$
Answered by Joel578 last updated on 17/Feb/19

Answered by tm888 last updated on 18/Feb/19