Question Number 160136 by alcohol last updated on 25/Nov/21
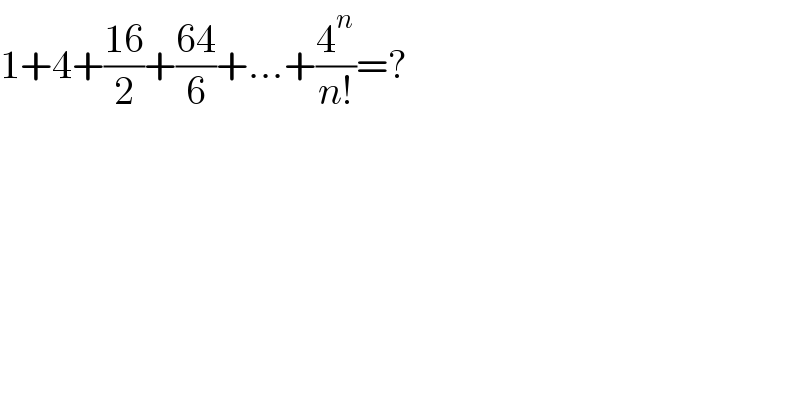
$$\mathrm{1}+\mathrm{4}+\frac{\mathrm{16}}{\mathrm{2}}+\frac{\mathrm{64}}{\mathrm{6}}+…+\frac{\mathrm{4}^{{n}} }{{n}!}=? \\ $$
Answered by puissant last updated on 25/Nov/21
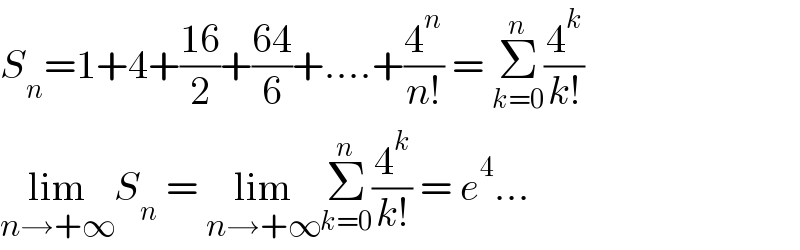
$${S}_{{n}} =\mathrm{1}+\mathrm{4}+\frac{\mathrm{16}}{\mathrm{2}}+\frac{\mathrm{64}}{\mathrm{6}}+….+\frac{\mathrm{4}^{{n}} }{{n}!}\:=\:\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\mathrm{4}^{{k}} }{{k}!} \\ $$$$\underset{{n}\rightarrow+\infty} {\mathrm{lim}}{S}_{{n}} \:=\:\underset{{n}\rightarrow+\infty} {\mathrm{lim}}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\mathrm{4}^{{k}} }{{k}!}\:=\:{e}^{\mathrm{4}} … \\ $$
