Question Number 24355 by ahmetbak1r last updated on 16/Nov/17
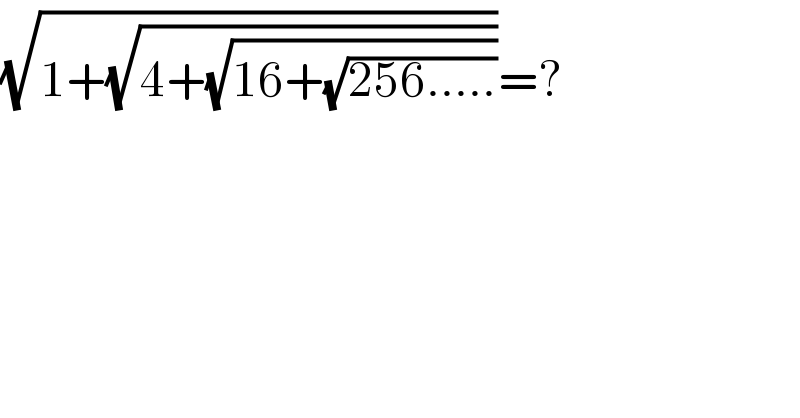
$$\sqrt{\mathrm{1}+\sqrt{\mathrm{4}+\sqrt{\mathrm{16}+\sqrt{\mathrm{256}…..}}}}=? \\ $$
Answered by ajfour last updated on 16/Nov/17
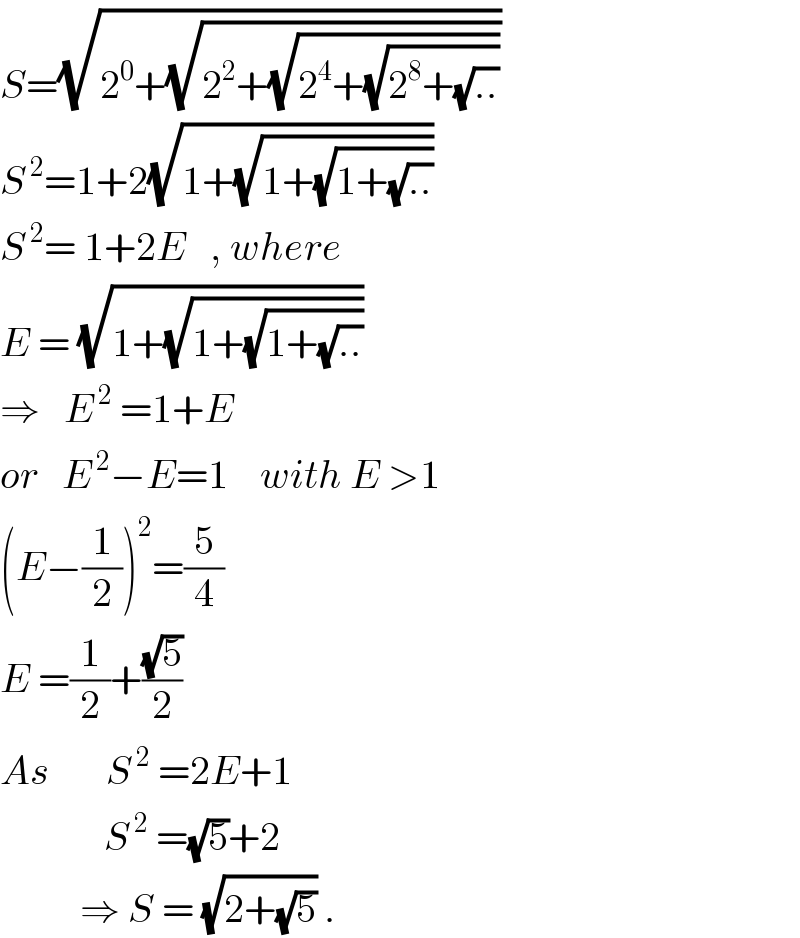
$${S}=\sqrt{\mathrm{2}^{\mathrm{0}} +\sqrt{\mathrm{2}^{\mathrm{2}} +\sqrt{\mathrm{2}^{\mathrm{4}} +\sqrt{\mathrm{2}^{\mathrm{8}} +\sqrt{..}}}}} \\ $$$${S}^{\:\mathrm{2}} =\mathrm{1}+\mathrm{2}\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+\sqrt{..}}}} \\ $$$${S}^{\:\mathrm{2}} =\:\mathrm{1}+\mathrm{2}{E}\:\:\:,\:{where} \\ $$$${E}\:=\:\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+\sqrt{..}}}} \\ $$$$\Rightarrow\:\:\:{E}^{\:\mathrm{2}} \:=\mathrm{1}+{E} \\ $$$${or}\:\:\:{E}^{\:\mathrm{2}} −{E}=\mathrm{1}\:\:\:\:{with}\:{E}\:>\mathrm{1} \\ $$$$\left({E}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{\mathrm{5}}{\mathrm{4}} \\ $$$${E}\:=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${As}\:\:\:\:\:\:\:{S}^{\:\mathrm{2}} \:=\mathrm{2}{E}+\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{S}^{\:\mathrm{2}} \:=\sqrt{\mathrm{5}}+\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\Rightarrow\:{S}\:=\:\sqrt{\mathrm{2}+\sqrt{\mathrm{5}}}\:. \\ $$
