Question Number 148452 by mathdanisur last updated on 28/Jul/21
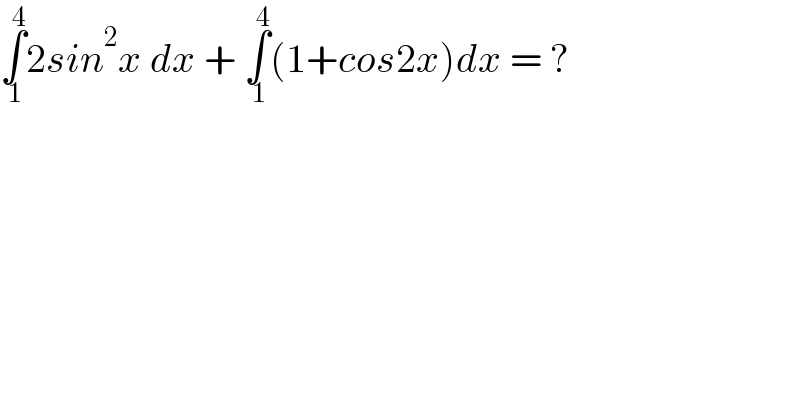
$$\underset{\:\mathrm{1}} {\overset{\:\mathrm{4}} {\int}}\mathrm{2}{sin}^{\mathrm{2}} {x}\:{dx}\:+\:\underset{\:\mathrm{1}} {\overset{\:\mathrm{4}} {\int}}\left(\mathrm{1}+{cos}\mathrm{2}{x}\right){dx}\:=\:? \\ $$
Answered by puissant last updated on 28/Jul/21
![=∫_1 ^4 2(((1−cos2x)/2))+(1+cos2x)dx =∫_1 ^4 (1−cos2x+1+cos2x)dx =∫_1 ^4 2dx = 2[x]_1 ^4 =2(4−1) I = 6...](https://www.tinkutara.com/question/Q148458.png)
$$=\int_{\mathrm{1}} ^{\mathrm{4}} \mathrm{2}\left(\frac{\mathrm{1}−\mathrm{cos2x}}{\mathrm{2}}\right)+\left(\mathrm{1}+\mathrm{cos2x}\right)\mathrm{dx} \\ $$$$=\int_{\mathrm{1}} ^{\mathrm{4}} \left(\mathrm{1}−\mathrm{cos2x}+\mathrm{1}+\mathrm{cos2x}\right)\mathrm{dx} \\ $$$$=\int_{\mathrm{1}} ^{\mathrm{4}} \mathrm{2dx}\:=\:\mathrm{2}\left[\mathrm{x}\right]_{\mathrm{1}} ^{\mathrm{4}} =\mathrm{2}\left(\mathrm{4}−\mathrm{1}\right) \\ $$$$\mathrm{I}\:=\:\mathrm{6}… \\ $$
Commented by mathdanisur last updated on 28/Jul/21

$${Thank}\:{you}\:{Ser} \\ $$
Answered by Ar Brandon last updated on 28/Jul/21
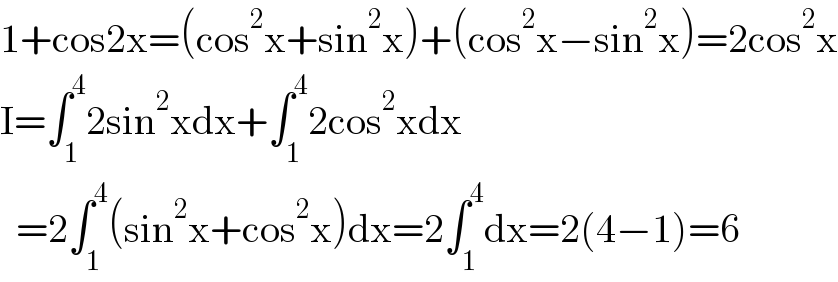
$$\mathrm{1}+\mathrm{cos2x}=\left(\mathrm{cos}^{\mathrm{2}} \mathrm{x}+\mathrm{sin}^{\mathrm{2}} \mathrm{x}\right)+\left(\mathrm{cos}^{\mathrm{2}} \mathrm{x}−\mathrm{sin}^{\mathrm{2}} \mathrm{x}\right)=\mathrm{2cos}^{\mathrm{2}} \mathrm{x} \\ $$$$\mathrm{I}=\int_{\mathrm{1}} ^{\mathrm{4}} \mathrm{2sin}^{\mathrm{2}} \mathrm{xdx}+\int_{\mathrm{1}} ^{\mathrm{4}} \mathrm{2cos}^{\mathrm{2}} \mathrm{xdx} \\ $$$$\:\:=\mathrm{2}\int_{\mathrm{1}} ^{\mathrm{4}} \left(\mathrm{sin}^{\mathrm{2}} \mathrm{x}+\mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)\mathrm{dx}=\mathrm{2}\int_{\mathrm{1}} ^{\mathrm{4}} \mathrm{dx}=\mathrm{2}\left(\mathrm{4}−\mathrm{1}\right)=\mathrm{6} \\ $$
Commented by mathdanisur last updated on 28/Jul/21

$${Thank}\:{you}\:{Ser} \\ $$
