Question Number 181840 by srikanth2684 last updated on 01/Dec/22

$$\underset{−\mathrm{1}} {\overset{\mathrm{4}} {\int}}{ln}\:{x}\:{dx} \\ $$
Commented by mr W last updated on 01/Dec/22
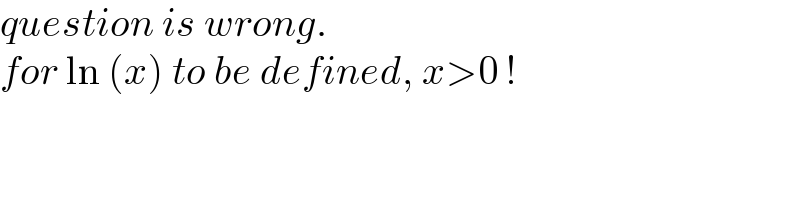
$${question}\:{is}\:{wrong}.\: \\ $$$${for}\:\mathrm{ln}\:\left({x}\right)\:{to}\:{be}\:{defined},\:{x}>\mathrm{0}\:! \\ $$
Commented by CElcedricjunior last updated on 01/Dec/22
![∫_(−1) ^4 lnxdx=[xln∣x∣−x]_(−1) ^4 =+∞](https://www.tinkutara.com/question/Q181844.png)
$$\int_{−\mathrm{1}} ^{\mathrm{4}} \boldsymbol{{lnxdx}}=\left[\boldsymbol{{xln}}\mid\boldsymbol{{x}}\mid−{x}\right]_{−\mathrm{1}} ^{\mathrm{4}} =+\infty \\ $$
Commented by Frix last updated on 01/Dec/22
![+∞ is wrong! ∫(dx/x)=ln ∣x∣ +C In this case the absolute value makes sense because obviously the area between the graph of y=(1/x) and the x−axis is the same in both intervals [a, b] and [−b, −a] ⇒ ∫_(−r) ^(+r) (dx/x)=0∀r∈R despite of the singularity. ∫ln x dx=−x(1−ln x)+C In this case y=ln x is not defined for x≤0 and x, y∈R If we let x, y∈C: x<0∧r=∣x∣ ⇔ x=re^(iπ) and ln x =ln r +πi ⇒ ∫_(−1) ^4 ln x dx=−5+8ln 2 +πi [real (ln x) =ln ∣x∣; imag (ln x) =((π(1−sign x))/2)]](https://www.tinkutara.com/question/Q181870.png)
$$+\infty\:\mathrm{is}\:\mathrm{wrong}! \\ $$$$\int\frac{{dx}}{{x}}=\mathrm{ln}\:\mid{x}\mid\:+{C} \\ $$$$\mathrm{In}\:\mathrm{this}\:\mathrm{case}\:\mathrm{the}\:\mathrm{absolute}\:\mathrm{value}\:\mathrm{makes}\:\mathrm{sense} \\ $$$$\mathrm{because}\:\mathrm{obviously}\:\mathrm{the}\:\mathrm{area}\:\mathrm{between}\:\mathrm{the} \\ $$$$\mathrm{graph}\:\mathrm{of}\:{y}=\frac{\mathrm{1}}{{x}}\:\mathrm{and}\:\mathrm{the}\:{x}−\mathrm{axis}\:\mathrm{is}\:\mathrm{the}\:\mathrm{same} \\ $$$$\mathrm{in}\:\mathrm{both}\:\mathrm{intervals}\:\left[{a},\:{b}\right]\:\mathrm{and}\:\left[−{b},\:−{a}\right]\:\Rightarrow \\ $$$$\underset{−{r}} {\overset{+{r}} {\int}}\frac{{dx}}{{x}}=\mathrm{0}\forall{r}\in\mathbb{R}\:\mathrm{despite}\:\mathrm{of}\:\mathrm{the}\:\mathrm{singularity}. \\ $$$$\int\mathrm{ln}\:{x}\:{dx}=−{x}\left(\mathrm{1}−\mathrm{ln}\:{x}\right)+{C} \\ $$$$\mathrm{In}\:\mathrm{this}\:\mathrm{case}\:{y}=\mathrm{ln}\:{x}\:\mathrm{is}\:\mathrm{not}\:\mathrm{defined}\:\mathrm{for}\:{x}\leqslant\mathrm{0} \\ $$$$\mathrm{and}\:{x},\:{y}\in\mathbb{R} \\ $$$$\mathrm{If}\:\mathrm{we}\:\mathrm{let}\:{x},\:{y}\in\mathbb{C}:\:{x}<\mathrm{0}\wedge{r}=\mid{x}\mid\:\Leftrightarrow\:{x}={r}\mathrm{e}^{\mathrm{i}\pi} \:\mathrm{and} \\ $$$$\mathrm{ln}\:{x}\:=\mathrm{ln}\:{r}\:+\pi\mathrm{i}\:\Rightarrow \\ $$$$\underset{−\mathrm{1}} {\overset{\mathrm{4}} {\int}}\mathrm{ln}\:{x}\:{dx}=−\mathrm{5}+\mathrm{8ln}\:\mathrm{2}\:+\pi\mathrm{i} \\ $$$$\left[\mathrm{real}\:\left(\mathrm{ln}\:{x}\right)\:=\mathrm{ln}\:\mid{x}\mid;\:\mathrm{imag}\:\left(\mathrm{ln}\:{x}\right)\:=\frac{\pi\left(\mathrm{1}−\mathrm{sign}\:{x}\right)}{\mathrm{2}}\right] \\ $$
