Question Number 96161 by bemath last updated on 30/May/20
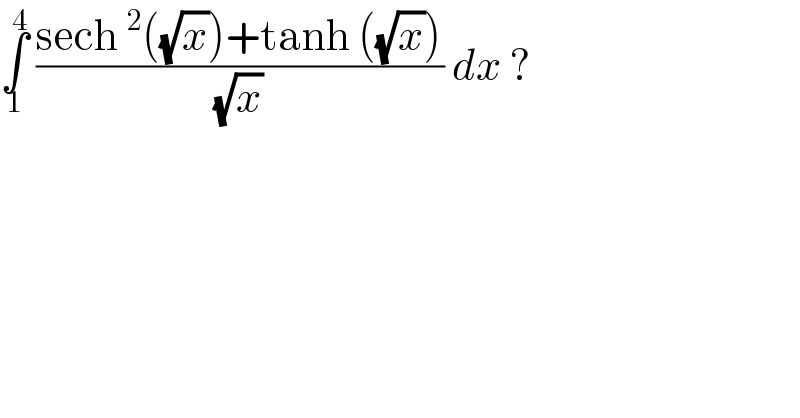
$$\underset{\mathrm{1}} {\overset{\mathrm{4}} {\int}}\:\frac{\mathrm{sech}\:^{\mathrm{2}} \left(\sqrt{{x}}\right)+\mathrm{tanh}\:\left(\sqrt{{x}}\right)}{\:\sqrt{{x}}\:}\:{dx}\:? \\ $$
Commented by bemath last updated on 30/May/20

$$\mathrm{thanks} \\ $$
Answered by bobhans last updated on 30/May/20
![let I_1 = ∫_1 ^4 ((sech^2 ((√x)) dx)/( (√x))) = 2 ∫_1 ^4 d(tanh (√x)) = 2 tanh (√x) ] _2^4 = 2(tanh (2)−tanh (1)) = 2{((e^2 −e^(−2) )/(e^2 +e^(−2) ))−((e−e^(−1) )/(e+e^(−1) )) }=2{((e^4 −1)/(e^4 +1)) − ((e^2 −1)/(e^2 +1)) } let I_2 = ∫_2 ^4 ((tanh (√x))/( (√x))) dx = 2 ln (cosh (√x)) ]_1 ^4 =2 ln (((e^2 +e^(−2) )/2))−2ln(((e+e^(−1) )/2)) = 2 ln (((e^2 +e^(−2) )/(e+e^(−1) ))) = 2ln (((e^4 +1)/(e^3 +e))) then I = I_1 +I_(2 ) = 2{((e^4 −1)/(e^4 +1))−((e^2 −1)/(e^2 +1))}+ 2 ln(((e^4 +1)/(e^3 +e)))](https://www.tinkutara.com/question/Q96164.png)
$$\mathrm{let}\:\mathrm{I}_{\mathrm{1}} \:=\:\underset{\mathrm{1}} {\overset{\mathrm{4}} {\int}}\:\frac{\mathrm{sech}\:^{\mathrm{2}} \left(\sqrt{{x}}\right)\:{dx}}{\:\sqrt{{x}}}\:=\:\mathrm{2}\:\underset{\mathrm{1}} {\overset{\mathrm{4}} {\int}}\:{d}\left(\mathrm{tanh}\:\sqrt{{x}}\right) \\ $$$$\left.=\:\mathrm{2}\:\mathrm{tanh}\:\sqrt{{x}}\:\right]\:_{\mathrm{2}} ^{\mathrm{4}} \:=\:\mathrm{2}\left(\mathrm{tanh}\:\left(\mathrm{2}\right)−\mathrm{tanh}\:\left(\mathrm{1}\right)\right) \\ $$$$=\:\mathrm{2}\left\{\frac{{e}^{\mathrm{2}} −{e}^{−\mathrm{2}} }{{e}^{\mathrm{2}} +{e}^{−\mathrm{2}} }−\frac{{e}−{e}^{−\mathrm{1}} }{{e}+{e}^{−\mathrm{1}} }\:\right\}=\mathrm{2}\left\{\frac{{e}^{\mathrm{4}} −\mathrm{1}}{{e}^{\mathrm{4}} +\mathrm{1}}\:−\:\frac{{e}^{\mathrm{2}} −\mathrm{1}}{{e}^{\mathrm{2}} +\mathrm{1}}\:\right\} \\ $$$$\left.\mathrm{let}\:\mathrm{I}_{\mathrm{2}} \:=\:\underset{\mathrm{2}} {\overset{\mathrm{4}} {\int}}\:\frac{\mathrm{tanh}\:\sqrt{{x}}}{\:\sqrt{{x}}}\:{dx}\:=\:\mathrm{2}\:\mathrm{ln}\:\left(\mathrm{cosh}\:\sqrt{{x}}\right)\:\right]_{\mathrm{1}} ^{\mathrm{4}} \\ $$$$=\mathrm{2}\:\mathrm{ln}\:\left(\frac{{e}^{\mathrm{2}} +{e}^{−\mathrm{2}} }{\mathrm{2}}\right)−\mathrm{2ln}\left(\frac{\mathrm{e}+\mathrm{e}^{−\mathrm{1}} }{\mathrm{2}}\right) \\ $$$$=\:\mathrm{2}\:\mathrm{ln}\:\left(\frac{\mathrm{e}^{\mathrm{2}} +\mathrm{e}^{−\mathrm{2}} }{\mathrm{e}+\mathrm{e}^{−\mathrm{1}} }\right)\:=\:\mathrm{2ln}\:\left(\frac{\mathrm{e}^{\mathrm{4}} +\mathrm{1}}{\mathrm{e}^{\mathrm{3}} +\mathrm{e}}\right)\: \\ $$$$\mathrm{then}\:\mathrm{I}\:=\:\mathrm{I}_{\mathrm{1}} +\mathrm{I}_{\mathrm{2}\:} =\:\mathrm{2}\left\{\frac{\mathrm{e}^{\mathrm{4}} −\mathrm{1}}{\mathrm{e}^{\mathrm{4}} +\mathrm{1}}−\frac{\mathrm{e}^{\mathrm{2}} −\mathrm{1}}{\mathrm{e}^{\mathrm{2}} +\mathrm{1}}\right\}+\:\mathrm{2}\:\mathrm{ln}\left(\frac{\mathrm{e}^{\mathrm{4}} +\mathrm{1}}{\mathrm{e}^{\mathrm{3}} +\mathrm{e}}\right)\: \\ $$
