Question Number 160013 by Odhiambojr last updated on 23/Nov/21
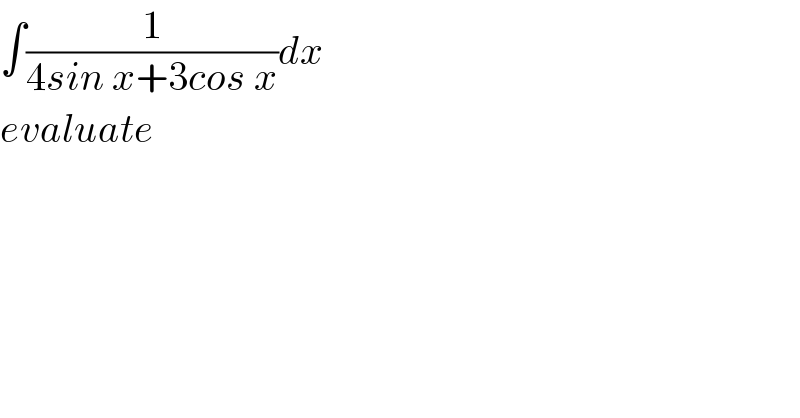
$$\int\frac{\mathrm{1}}{\mathrm{4}{sin}\:{x}+\mathrm{3}{cos}\:{x}}{dx} \\ $$$${evaluate} \\ $$
Commented by tounghoungko last updated on 23/Nov/21
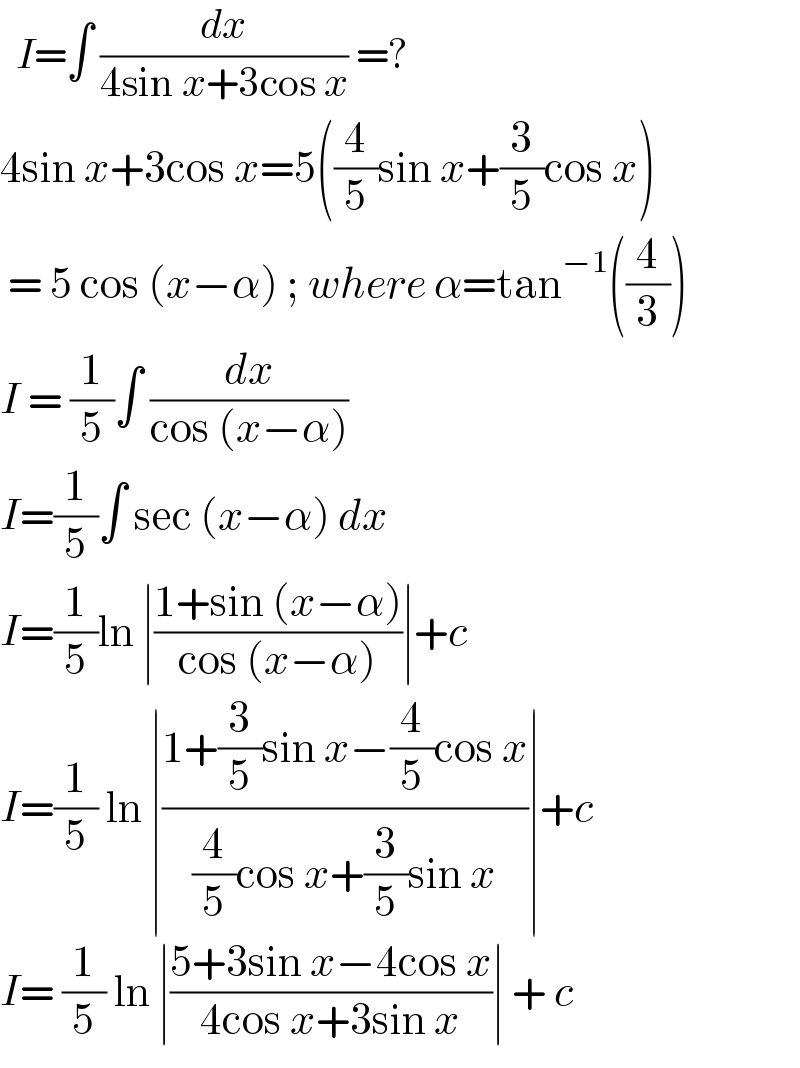
$$\:\:{I}=\int\:\frac{{dx}}{\mathrm{4sin}\:{x}+\mathrm{3cos}\:{x}}\:=? \\ $$$$\mathrm{4sin}\:{x}+\mathrm{3cos}\:{x}=\mathrm{5}\left(\frac{\mathrm{4}}{\mathrm{5}}\mathrm{sin}\:{x}+\frac{\mathrm{3}}{\mathrm{5}}\mathrm{cos}\:{x}\right) \\ $$$$\:=\:\mathrm{5}\:\mathrm{cos}\:\left({x}−\alpha\right)\:;\:{where}\:\alpha=\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{4}}{\mathrm{3}}\right) \\ $$$${I}\:=\:\frac{\mathrm{1}}{\mathrm{5}}\int\:\frac{{dx}}{\mathrm{cos}\:\left({x}−\alpha\right)}\: \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{5}}\int\:\mathrm{sec}\:\left({x}−\alpha\right)\:{dx} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{5}}\mathrm{ln}\:\mid\frac{\mathrm{1}+\mathrm{sin}\:\left({x}−\alpha\right)}{\mathrm{cos}\:\left({x}−\alpha\right)}\mid+{c} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{5}}\:\mathrm{ln}\:\mid\frac{\mathrm{1}+\frac{\mathrm{3}}{\mathrm{5}}\mathrm{sin}\:{x}−\frac{\mathrm{4}}{\mathrm{5}}\mathrm{cos}\:{x}}{\frac{\mathrm{4}}{\mathrm{5}}\mathrm{cos}\:{x}+\frac{\mathrm{3}}{\mathrm{5}}\mathrm{sin}\:{x}}\mid+{c} \\ $$$${I}=\:\frac{\mathrm{1}}{\mathrm{5}}\:\mathrm{ln}\:\mid\frac{\mathrm{5}+\mathrm{3sin}\:{x}−\mathrm{4cos}\:{x}}{\mathrm{4cos}\:{x}+\mathrm{3sin}\:{x}}\mid\:+\:{c} \\ $$
