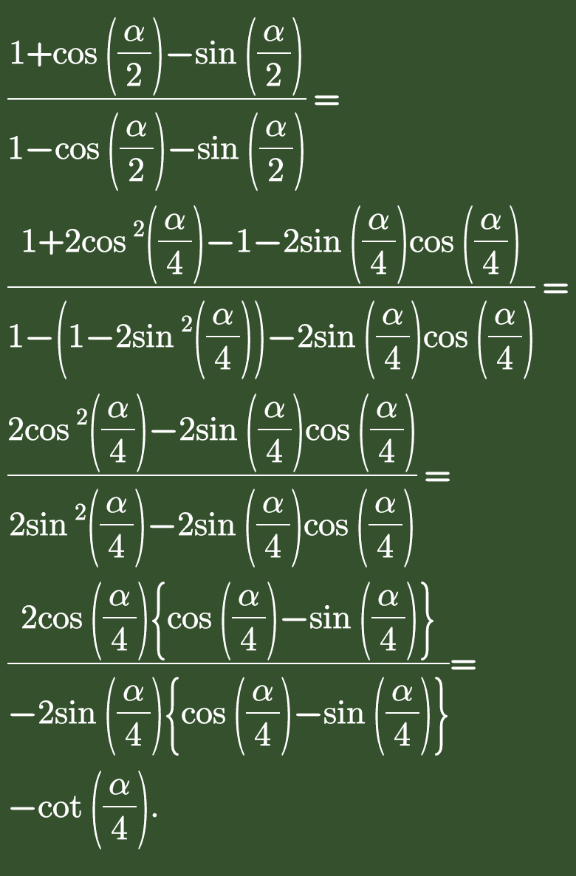Question Number 110897 by bemath last updated on 31/Aug/20
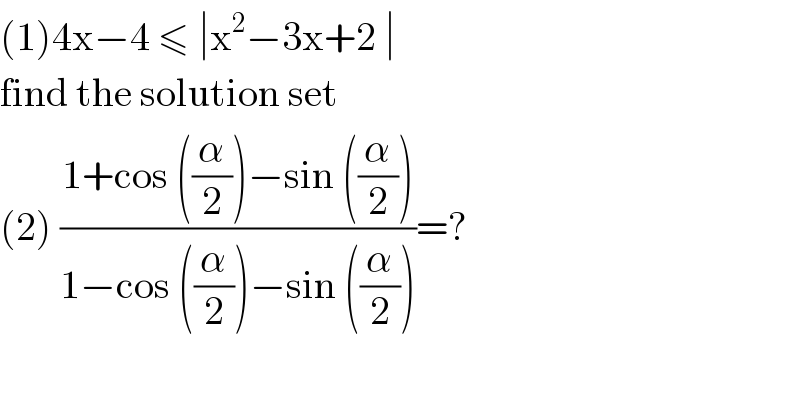
$$\left(\mathrm{1}\right)\mathrm{4x}−\mathrm{4}\:\leqslant\:\mid\mathrm{x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{2}\:\mid\: \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{set}\: \\ $$$$\left(\mathrm{2}\right)\:\frac{\mathrm{1}+\mathrm{cos}\:\left(\frac{\alpha}{\mathrm{2}}\right)−\mathrm{sin}\:\left(\frac{\alpha}{\mathrm{2}}\right)}{\mathrm{1}−\mathrm{cos}\:\left(\frac{\alpha}{\mathrm{2}}\right)−\mathrm{sin}\:\left(\frac{\alpha}{\mathrm{2}}\right)}=? \\ $$
Answered by john santu last updated on 31/Aug/20

Answered by Dwaipayan Shikari last updated on 31/Aug/20
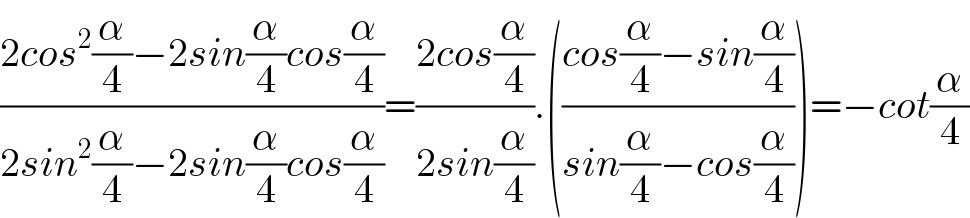
$$\frac{\mathrm{2}{cos}^{\mathrm{2}} \frac{\alpha}{\mathrm{4}}−\mathrm{2}{sin}\frac{\alpha}{\mathrm{4}}{cos}\frac{\alpha}{\mathrm{4}}}{\mathrm{2}{sin}^{\mathrm{2}} \frac{\alpha}{\mathrm{4}}−\mathrm{2}{sin}\frac{\alpha}{\mathrm{4}}{cos}\frac{\alpha}{\mathrm{4}}}=\frac{\mathrm{2}{cos}\frac{\alpha}{\mathrm{4}}}{\mathrm{2}{sin}\frac{\alpha}{\mathrm{4}}}.\left(\frac{{cos}\frac{\alpha}{\mathrm{4}}−{sin}\frac{\alpha}{\mathrm{4}}}{{sin}\frac{\alpha}{\mathrm{4}}−{cos}\frac{\alpha}{\mathrm{4}}}\right)=−{cot}\frac{\alpha}{\mathrm{4}} \\ $$
Answered by bemath last updated on 31/Aug/20