Menu Close

1-5-2-15-a-b-5-2-find-a-b-

Tinku Tara 0 Comments
Pin




Question Number 182627 by manxsol last updated on 12/Dec/22
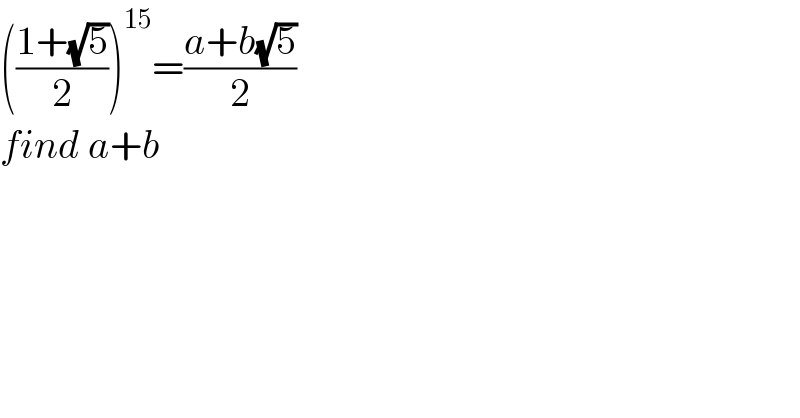
(((1+(√5))/2))^(15) =((a+b(√5))/2) find a+b
$$\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{15}} =\frac{{a}+{b}\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${find}\:{a}+{b} \\ $$
Answered by Rasheed.Sindhi last updated on 12/Dec/22
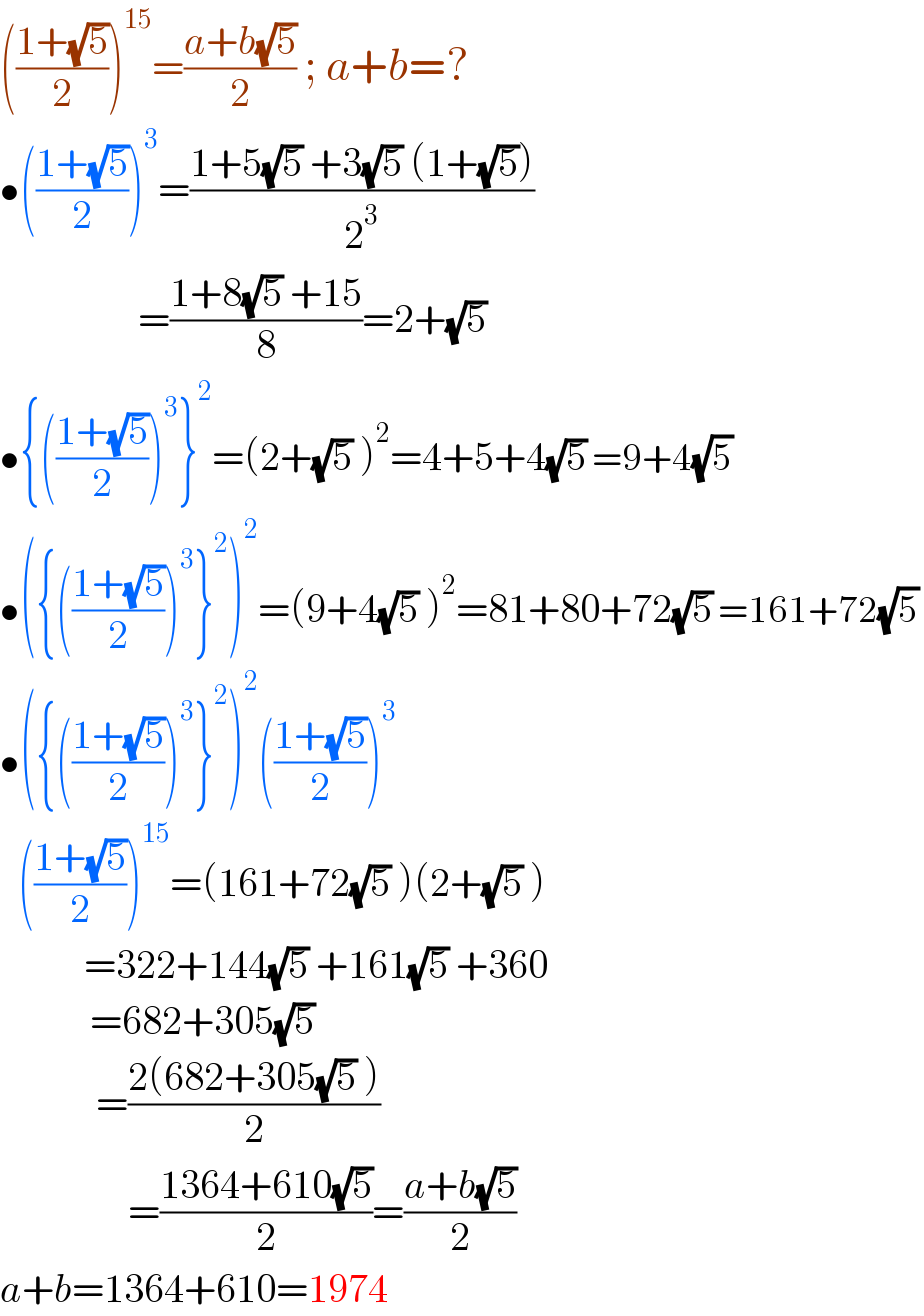
(((1+(√5))/2))^(15) =((a+b(√5))/2) ; a+b=? •(((1+(√5))/2))^3 =((1+5(√5) +3(√5) (1+(√5)))/2^3 ) =((1+8(√5) +15)/8)=2+(√5) •{(((1+(√5))/2))^3 }^2 =(2+(√5) )^2 =4+5+4(√5) =9+4(√5) •({(((1+(√5))/2))^3 }^2 )^2 =(9+4(√5) )^2 =81+80+72(√5) =161+72(√5) •({(((1+(√5))/2))^3 }^2 )^2 (((1+(√5))/2))^3 (((1+(√5))/2))^(15) =(161+72(√5) )(2+(√5) ) =322+144(√5) +161(√5) +360 =682+305(√5) =((2(682+305(√5) ))/2) =((1364+610(√5))/2)=((a+b(√5))/2) a+b=1364+610=1974
$$\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{15}} =\frac{{a}+{b}\sqrt{\mathrm{5}}}{\mathrm{2}}\:;\:{a}+{b}=? \\ $$$$\bullet\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{3}} =\frac{\mathrm{1}+\mathrm{5}\sqrt{\mathrm{5}}\:+\mathrm{3}\sqrt{\mathrm{5}}\:\left(\mathrm{1}+\sqrt{\mathrm{5}}\right)}{\mathrm{2}^{\mathrm{3}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}+\mathrm{8}\sqrt{\mathrm{5}}\:+\mathrm{15}}{\mathrm{8}}=\mathrm{2}+\sqrt{\mathrm{5}} \\ $$$$\bullet\left\{\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{3}} \right\}^{\mathrm{2}} =\left(\mathrm{2}+\sqrt{\mathrm{5}}\:\right)^{\mathrm{2}} =\mathrm{4}+\mathrm{5}+\mathrm{4}\sqrt{\mathrm{5}}\:=\mathrm{9}+\mathrm{4}\sqrt{\mathrm{5}}\:\: \\ $$$$\bullet\left(\left\{\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{3}} \right\}^{\mathrm{2}} \right)^{\mathrm{2}} =\left(\mathrm{9}+\mathrm{4}\sqrt{\mathrm{5}}\:\right)^{\mathrm{2}} =\mathrm{81}+\mathrm{80}+\mathrm{72}\sqrt{\mathrm{5}}\:=\mathrm{161}+\mathrm{72}\sqrt{\mathrm{5}}\: \\ $$$$\bullet\left(\left\{\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{3}} \right\}^{\mathrm{2}} \right)^{\mathrm{2}} \left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{3}} \\ $$$$\:\:\:\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{15}} =\left(\mathrm{161}+\mathrm{72}\sqrt{\mathrm{5}}\:\right)\left(\mathrm{2}+\sqrt{\mathrm{5}}\:\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{322}+\mathrm{144}\sqrt{\mathrm{5}}\:+\mathrm{161}\sqrt{\mathrm{5}}\:+\mathrm{360} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{682}+\mathrm{305}\sqrt{\mathrm{5}}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{2}\left(\mathrm{682}+\mathrm{305}\sqrt{\mathrm{5}}\:\right)}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1364}+\mathrm{610}\sqrt{\mathrm{5}}}{\mathrm{2}}=\frac{{a}+{b}\sqrt{\mathrm{5}}}{\mathrm{2}}\: \\ $$$${a}+{b}=\mathrm{1364}+\mathrm{610}=\mathrm{1974} \\ $$
Commented by manxsol last updated on 12/Dec/22
thanks,Sir. Rasheed for work . it is my gift (((1+(√5))/2))^(15) =((1364+610(√5))/2) serie de finonacci determinant ((1,2,3,4,5,6,7,8,9,(10),(11),(12),(13),(14),(15 ),(16)),(1,1,2,3,5,8,(13),(21),(34),(55),(89),(144),(233),(377),(610),(987))) a=610 b=377+987=1364 deduccion hecha de tabla de potencias de Φ=(1+(√5))/2
$${thanks},{Sir}.\:{Rasheed}\:{for}\:{work} \\ $$$$.\:{it}\:{is}\:{my}\:{gift} \\ $$$$ \\ $$$$\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{15}} \:\:=\frac{\mathrm{1364}+\mathrm{610}\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${serie}\:{de}\:{finonacci} \\ $$$$\begin{array}{|c|c|}{\mathrm{1}}&\hline{\mathrm{2}}&\hline{\mathrm{3}}&\hline{\mathrm{4}}&\hline{\mathrm{5}}&\hline{\mathrm{6}}&\hline{\mathrm{7}}&\hline{\mathrm{8}}&\hline{\mathrm{9}}&\hline{\mathrm{10}}&\hline{\mathrm{11}}&\hline{\mathrm{12}}&\hline{\mathrm{13}}&\hline{\mathrm{14}}&\hline{\mathrm{15}\:\:}&\hline{\mathrm{16}}\\{\mathrm{1}}&\hline{\mathrm{1}}&\hline{\mathrm{2}}&\hline{\mathrm{3}}&\hline{\mathrm{5}}&\hline{\mathrm{8}}&\hline{\mathrm{13}}&\hline{\mathrm{21}}&\hline{\mathrm{34}}&\hline{\mathrm{55}}&\hline{\mathrm{89}}&\hline{\mathrm{144}}&\hline{\mathrm{233}}&\hline{\mathrm{377}}&\hline{\mathrm{610}}&\hline{\mathrm{987}}\\\hline\end{array} \\ $$$$ \\ $$$${a}=\mathrm{610} \\ $$$${b}=\mathrm{377}+\mathrm{987}=\mathrm{1364} \\ $$$${deduccion}\:{hecha}\:{de}\:{tabla}\:{de} \\ $$$${potencias}\:{de}\:\Phi=\left(\mathrm{1}+\sqrt{\mathrm{5}}\right)/\mathrm{2} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by Rasheed.Sindhi last updated on 12/Dec/22
A nice gift! Thanks a lOt sir manxsol!
$$\boldsymbol{\mathrm{A}}\:\boldsymbol{\mathrm{nice}}\:\boldsymbol{\mathrm{gift}}! \\ $$$$\mathbb{T}\boldsymbol{\mathrm{han}}\Bbbk\boldsymbol{\mathrm{s}}\:\boldsymbol{\mathrm{a}}\:\boldsymbol{\mathrm{lOt}}\:\:\boldsymbol{\mathrm{sir}}\:\boldsymbol{\mathrm{manxsol}}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *