Question Number 128826 by benjo_mathlover last updated on 10/Jan/21
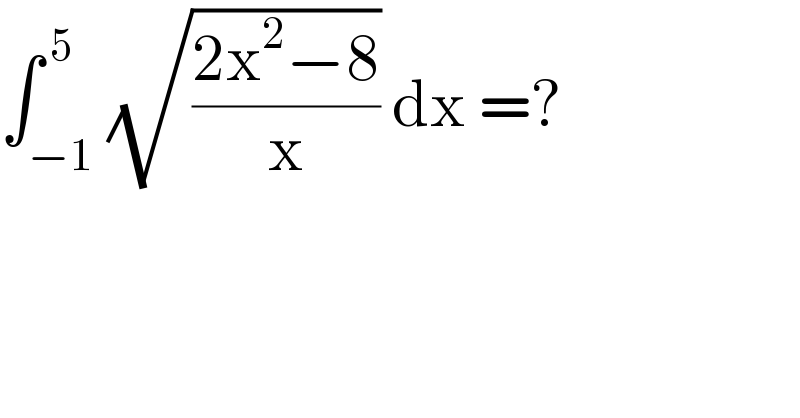
$$\int_{−\mathrm{1}} ^{\:\mathrm{5}} \sqrt{\frac{\mathrm{2x}^{\mathrm{2}} −\mathrm{8}}{\mathrm{x}}}\:\mathrm{dx}\:=? \\ $$
Answered by bobhans last updated on 10/Jan/21
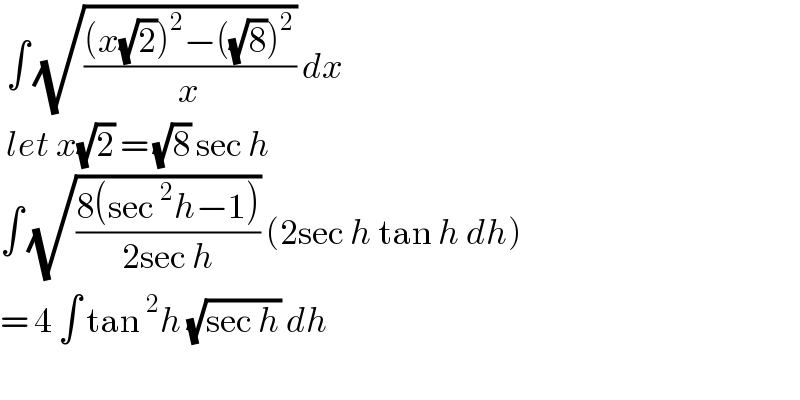
$$\:\int\:\sqrt{\frac{\left({x}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} −\left(\sqrt{\mathrm{8}}\right)^{\mathrm{2}} }{{x}}}\:{dx}\: \\ $$$$\:{let}\:{x}\sqrt{\mathrm{2}}\:=\:\sqrt{\mathrm{8}}\:\mathrm{sec}\:{h}\: \\ $$$$\int\:\sqrt{\frac{\mathrm{8}\left(\mathrm{sec}\:^{\mathrm{2}} {h}−\mathrm{1}\right)}{\mathrm{2sec}\:{h}}}\:\left(\mathrm{2sec}\:{h}\:\mathrm{tan}\:{h}\:{dh}\right) \\ $$$$=\:\mathrm{4}\:\int\:\mathrm{tan}\:^{\mathrm{2}} {h}\:\sqrt{\mathrm{sec}\:{h}}\:{dh}\: \\ $$$$ \\ $$
