Question Number 20873 by Joel577 last updated on 05/Sep/17

$$\int_{\mathrm{1}} ^{\mathrm{5}} \frac{{e}^{{x}} }{{x}^{\mathrm{2}} }\:{dx} \\ $$
Answered by alex041103 last updated on 08/Sep/17
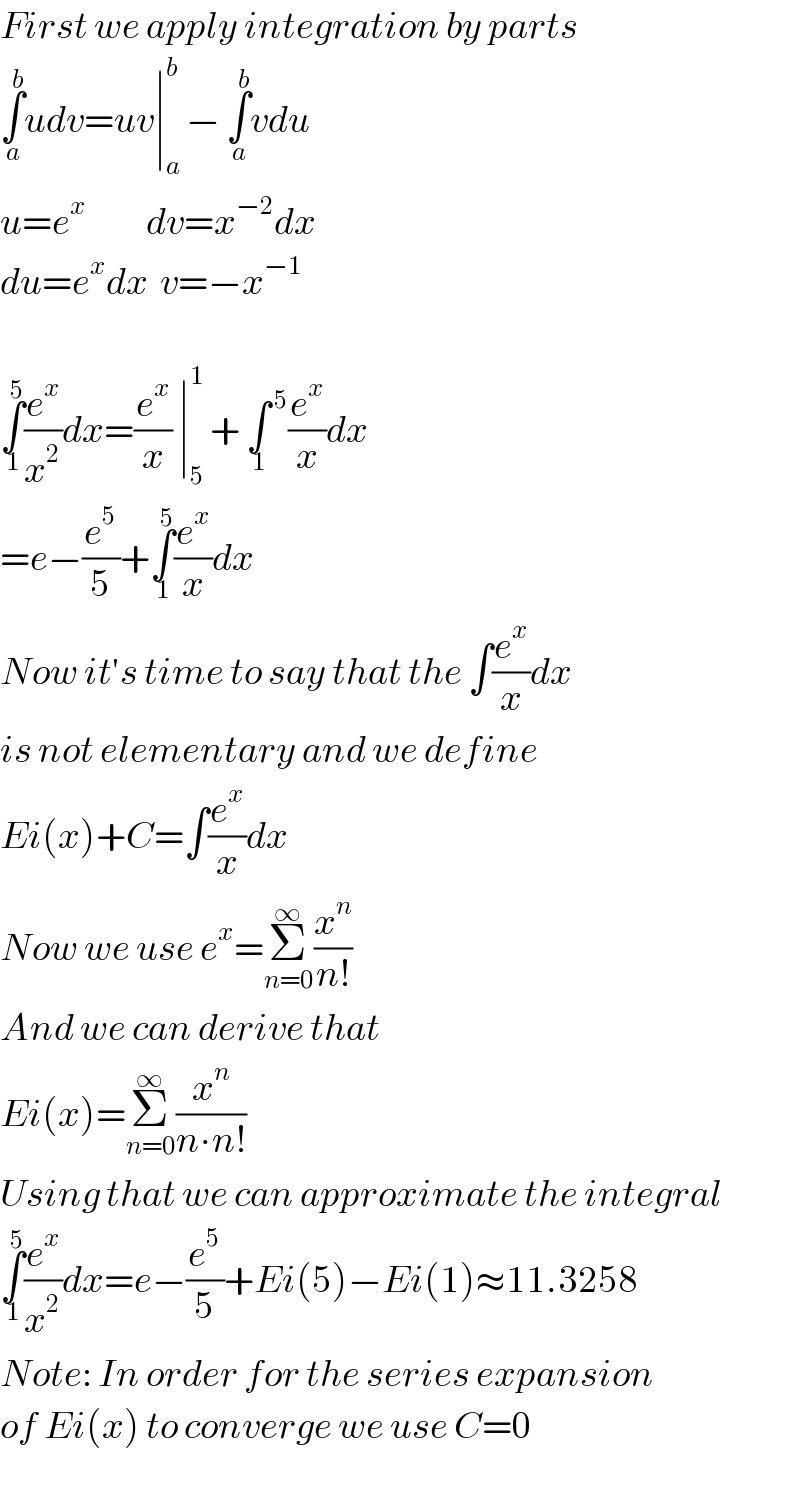
$${First}\:{we}\:{apply}\:{integration}\:{by}\:{parts} \\ $$$$\underset{\:{a}} {\overset{{b}} {\int}}{udv}={uv}\mid_{{a}} ^{{b}} \:−\:\underset{\:{a}} {\overset{{b}} {\int}}{vdu} \\ $$$${u}={e}^{{x}} \:\:\:\:\:\:\:\:\:\:{dv}={x}^{−\mathrm{2}} {dx} \\ $$$${du}={e}^{{x}} {dx}\:\:{v}=−{x}^{−\mathrm{1}} \\ $$$$ \\ $$$$\underset{\:\mathrm{1}} {\overset{\mathrm{5}} {\int}}\frac{{e}^{{x}} }{{x}^{\mathrm{2}} }{dx}=\frac{{e}^{{x}} }{{x}}\:\mid_{\mathrm{5}} ^{\mathrm{1}} \:+\:\underset{\:\mathrm{1}} {\int}^{\:\mathrm{5}} \frac{{e}^{{x}} }{{x}}{dx} \\ $$$$={e}−\frac{{e}^{\mathrm{5}} }{\mathrm{5}}+\underset{\:\mathrm{1}} {\overset{\mathrm{5}} {\int}}\frac{{e}^{{x}} }{{x}}{dx} \\ $$$${Now}\:{it}'{s}\:{time}\:{to}\:{say}\:{that}\:{the}\:\int\frac{{e}^{{x}} }{{x}}{dx} \\ $$$${is}\:{not}\:{elementary}\:{and}\:{we}\:{define} \\ $$$${Ei}\left({x}\right)+{C}=\int\frac{{e}^{{x}} }{{x}}{dx} \\ $$$${Now}\:{we}\:{use}\:{e}^{{x}} =\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}!} \\ $$$${And}\:{we}\:{can}\:{derive}\:{that} \\ $$$${Ei}\left({x}\right)=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}\centerdot{n}!} \\ $$$${Using}\:{that}\:{we}\:{can}\:{approximate}\:{the}\:{integral} \\ $$$$\underset{\:\mathrm{1}} {\overset{\mathrm{5}} {\int}}\frac{{e}^{{x}} }{{x}^{\mathrm{2}} }{dx}={e}−\frac{{e}^{\mathrm{5}} }{\mathrm{5}}+{Ei}\left(\mathrm{5}\right)−{Ei}\left(\mathrm{1}\right)\approx\mathrm{11}.\mathrm{3258} \\ $$$${Note}:\:{In}\:{order}\:{for}\:{the}\:{series}\:{expansion} \\ $$$${of}\:{Ei}\left({x}\right)\:{to}\:{converge}\:{we}\:{use}\:{C}=\mathrm{0} \\ $$
Commented by Joel577 last updated on 09/Sep/17
$${thank}\:{you}\:{very}\:{much} \\ $$$$ \\ $$
