1-6-1-8-1-1-6-1-4-1-1-6-1-1-

Question Number 146622 by mathdanisur last updated on 14/Jul/21

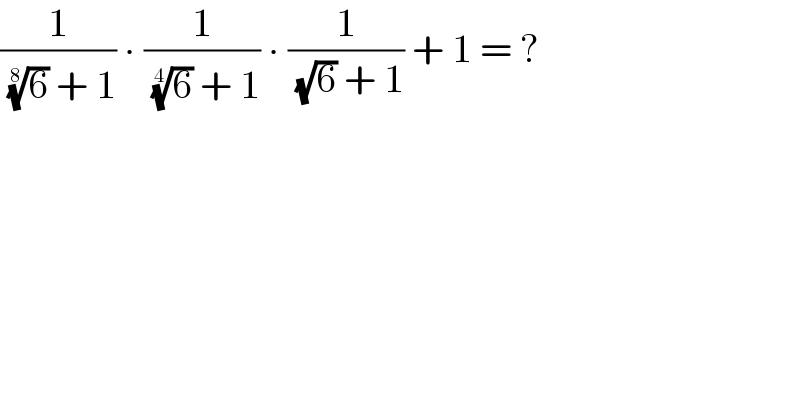
$$\frac{\mathrm{1}}{\:\sqrt[{\mathrm{8}}]{\mathrm{6}}\:+\:\mathrm{1}}\:\centerdot\:\frac{\mathrm{1}}{\:\sqrt[{\mathrm{4}}]{\mathrm{6}}\:+\:\mathrm{1}}\:\centerdot\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{6}}\:+\:\mathrm{1}}\:+\:\mathrm{1}\:=\:? \\ $$

Commented by hknkrc46 last updated on 14/Jul/21

★ (1/(((6)^(1/8) + 1)((6)^(1/4) + 1)((√6) + 1))) + 1 = (((6)^(1/8) − 1)/(((6)^(1/8) − 1)((6)^(1/8) + 1)_((6)^(1/4) − 1) ((6)^(1/4) + 1)((√6) + 1))) + 1 = (((6)^(1/8) − 1)/(((6)^(1/4) − 1)((6)^(1/4) + 1)_((√6) − 1) ((√6) + 1))) + 1 = (((6)^(1/8) − 1)/(((√6) − 1)((√6) + 1))) + 1 = (((6)^(1/8) − 1)/(6 − 1)) + 1 = (((6)^(1/8) − 1)/5) + 1 = (((6)^(1/8) + 4)/5)

$$\bigstar\:\frac{\mathrm{1}}{\left(\sqrt[{\mathrm{8}}]{\mathrm{6}}\:+\:\mathrm{1}\right)\left(\sqrt[{\mathrm{4}}]{\mathrm{6}}\:+\:\mathrm{1}\right)\left(\sqrt{\mathrm{6}}\:+\:\mathrm{1}\right)}\:+\:\mathrm{1} \\ $$$$=\:\frac{\sqrt[{\mathrm{8}}]{\mathrm{6}}\:−\:\mathrm{1}}{\underset{\sqrt[{\mathrm{4}}]{\mathrm{6}}\:−\:\mathrm{1}} {\underbrace{\left(\sqrt[{\mathrm{8}}]{\mathrm{6}}\:−\:\mathrm{1}\right)\left(\sqrt[{\mathrm{8}}]{\mathrm{6}}\:+\:\mathrm{1}\right)}}\left(\sqrt[{\mathrm{4}}]{\mathrm{6}}\:+\:\mathrm{1}\right)\left(\sqrt{\mathrm{6}}\:+\:\mathrm{1}\right)}\:+\:\mathrm{1} \\ $$$$=\:\frac{\sqrt[{\mathrm{8}}]{\mathrm{6}}\:−\:\mathrm{1}}{\underset{\sqrt{\mathrm{6}}\:−\:\mathrm{1}} {\underbrace{\left(\sqrt[{\mathrm{4}}]{\mathrm{6}}\:−\:\mathrm{1}\right)\left(\sqrt[{\mathrm{4}}]{\mathrm{6}}\:+\:\mathrm{1}\right)}}\left(\sqrt{\mathrm{6}}\:+\:\mathrm{1}\right)}\:+\:\mathrm{1} \\ $$$$=\:\frac{\sqrt[{\mathrm{8}}]{\mathrm{6}}\:−\:\mathrm{1}}{\left(\sqrt{\mathrm{6}}\:−\:\mathrm{1}\right)\left(\sqrt{\mathrm{6}}\:+\:\mathrm{1}\right)}\:+\:\mathrm{1}\: \\ $$$$=\:\frac{\sqrt[{\mathrm{8}}]{\mathrm{6}}\:−\:\mathrm{1}}{\mathrm{6}\:−\:\mathrm{1}}\:+\:\mathrm{1}\:=\:\frac{\sqrt[{\mathrm{8}}]{\mathrm{6}}\:−\:\mathrm{1}}{\mathrm{5}}\:+\:\mathrm{1}\: \\ $$$$=\:\frac{\sqrt[{\mathrm{8}}]{\mathrm{6}}\:+\:\mathrm{4}}{\mathrm{5}} \\ $$

Answered by som(math1967) last updated on 14/Jul/21

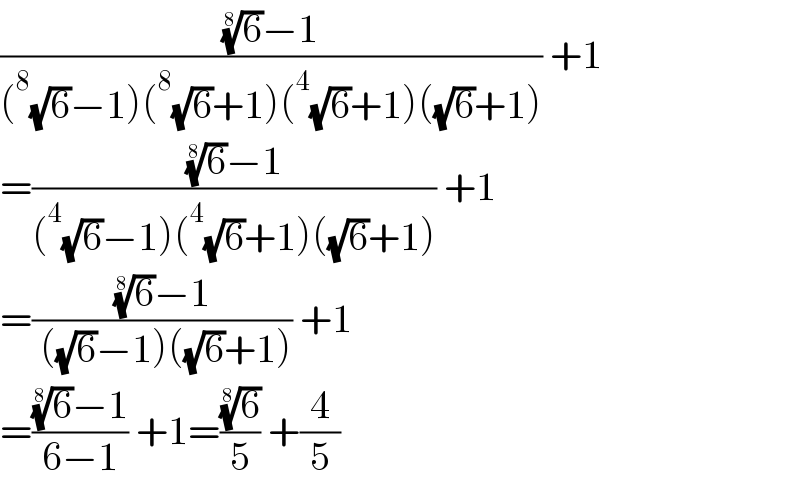
(((6)^(1/8) −1)/((^8 (√6)−1)(^8 (√6)+1)(^4 (√6)+1)((√6)+1))) +1 =(((6)^(1/8) −1)/((^4 (√6)−1)(^4 (√6)+1)((√6)+1))) +1 =(((6)^(1/8) −1)/( ((√6)−1)((√6)+1))) +1 =(((6)^(1/8) −1)/(6−1)) +1=((6)^(1/8) /5) +(4/5)

$$\frac{\sqrt[{\mathrm{8}}]{\mathrm{6}}−\mathrm{1}}{\left(^{\mathrm{8}} \sqrt{\mathrm{6}}−\mathrm{1}\right)\left(^{\mathrm{8}} \sqrt{\mathrm{6}}+\mathrm{1}\right)\left(^{\mathrm{4}} \sqrt{\mathrm{6}}+\mathrm{1}\right)\left(\sqrt{\mathrm{6}}+\mathrm{1}\right)}\:+\mathrm{1} \\ $$$$=\frac{\sqrt[{\mathrm{8}}]{\mathrm{6}}−\mathrm{1}}{\left(^{\mathrm{4}} \sqrt{\mathrm{6}}−\mathrm{1}\right)\left(^{\mathrm{4}} \sqrt{\mathrm{6}}+\mathrm{1}\right)\left(\sqrt{\mathrm{6}}+\mathrm{1}\right)}\:+\mathrm{1} \\ $$$$=\frac{\sqrt[{\mathrm{8}}]{\mathrm{6}}−\mathrm{1}}{\:\left(\sqrt{\mathrm{6}}−\mathrm{1}\right)\left(\sqrt{\mathrm{6}}+\mathrm{1}\right)}\:+\mathrm{1} \\ $$$$=\frac{\sqrt[{\mathrm{8}}]{\mathrm{6}}−\mathrm{1}}{\mathrm{6}−\mathrm{1}}\:+\mathrm{1}=\frac{\sqrt[{\mathrm{8}}]{\mathrm{6}}}{\mathrm{5}}\:+\frac{\mathrm{4}}{\mathrm{5}} \\ $$

Commented by mathdanisur last updated on 14/Jul/21

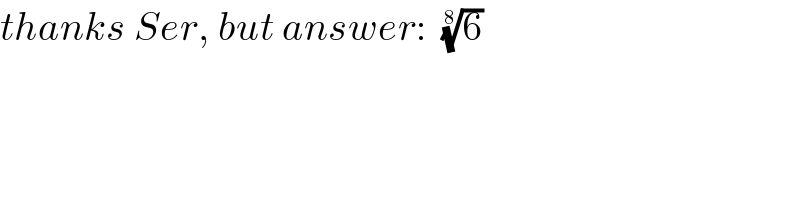
$${thanks}\:{Ser},\:{but}\:{answer}:\:\:\sqrt[{\mathrm{8}}]{\mathrm{6}} \\ $$

Commented by som(math1967) last updated on 14/Jul/21

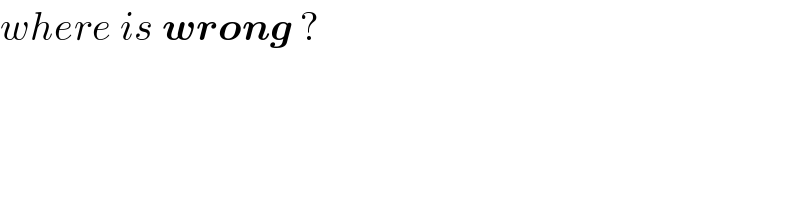
$${where}\:{is}\:\boldsymbol{{wrong}}\:? \\ $$

Commented by mathdanisur last updated on 14/Jul/21

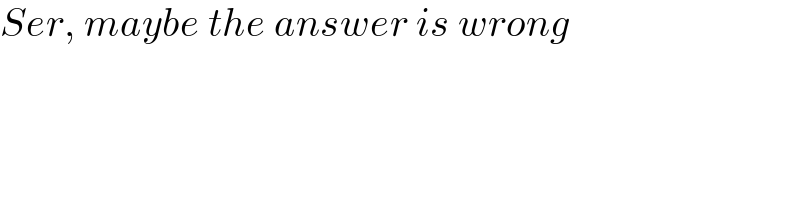
$${Ser},\:{maybe}\:{the}\:{answer}\:{is}\:{wrong} \\ $$

Commented by som(math1967) last updated on 14/Jul/21

let (1/((^8 (√6)+1)(^4 (√6)+1)((√6)+1))) +1=^8 (√6) (1/((^8 (√6)+1)(^4 (√6)+1)((√6)+1)))=^8 (√6)−1 (1/((^8 (√6)+1)(^4 (√6)+1)((√6)+1)(^8 (√6)−1)))=1 (1/(6−1))=1 ∴(1/5)=1 ?????? so I think ans is wrong

$${let}\:\frac{\mathrm{1}}{\left(^{\mathrm{8}} \sqrt{\mathrm{6}}+\mathrm{1}\right)\left(^{\mathrm{4}} \sqrt{\mathrm{6}}+\mathrm{1}\right)\left(\sqrt{\mathrm{6}}+\mathrm{1}\right)}\:+\mathrm{1}=^{\mathrm{8}} \sqrt{\mathrm{6}} \\ $$$$\frac{\mathrm{1}}{\left(^{\mathrm{8}} \sqrt{\mathrm{6}}+\mathrm{1}\right)\left(^{\mathrm{4}} \sqrt{\mathrm{6}}+\mathrm{1}\right)\left(\sqrt{\mathrm{6}}+\mathrm{1}\right)}=^{\mathrm{8}} \sqrt{\mathrm{6}}−\mathrm{1} \\ $$$$\frac{\mathrm{1}}{\left(^{\mathrm{8}} \sqrt{\mathrm{6}}+\mathrm{1}\right)\left(^{\mathrm{4}} \sqrt{\mathrm{6}}+\mathrm{1}\right)\left(\sqrt{\mathrm{6}}+\mathrm{1}\right)\left(^{\mathrm{8}} \sqrt{\mathrm{6}}−\mathrm{1}\right)}=\mathrm{1} \\ $$$$\frac{\mathrm{1}}{\mathrm{6}−\mathrm{1}}=\mathrm{1} \\ $$$$\therefore\frac{\mathrm{1}}{\mathrm{5}}=\mathrm{1}\:\:?????? \\ $$$${so}\:{I}\:{think}\:{ans}\:{is}\:{wrong} \\ $$

Commented by mathdanisur last updated on 14/Jul/21

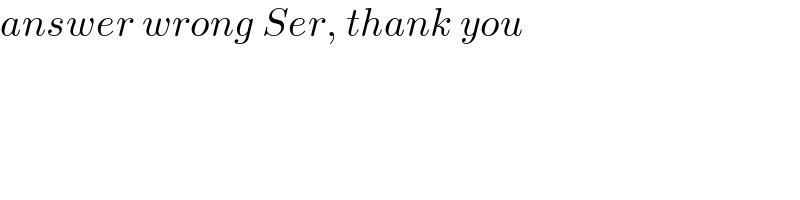
$${answer}\:{wrong}\:{Ser},\:{thank}\:{you} \\ $$

Facebook Tweet Pin

1-6-1-8-1-1-6-1-4-1-1-6-1-1-

Leave a Reply Cancel reply