Question Number 85875 by sakeefhasan05@gmail.com last updated on 25/Mar/20
![∫((1/(7[1−(1/7)e^x ]))) dx](https://www.tinkutara.com/question/Q85875.png)
$$\int\left(\frac{\mathrm{1}}{\mathrm{7}\left[\mathrm{1}−\frac{\mathrm{1}}{\mathrm{7}}\mathrm{e}^{\mathrm{x}} \right]}\right)\:\mathrm{dx} \\ $$
Answered by TANMAY PANACEA. last updated on 25/Mar/20
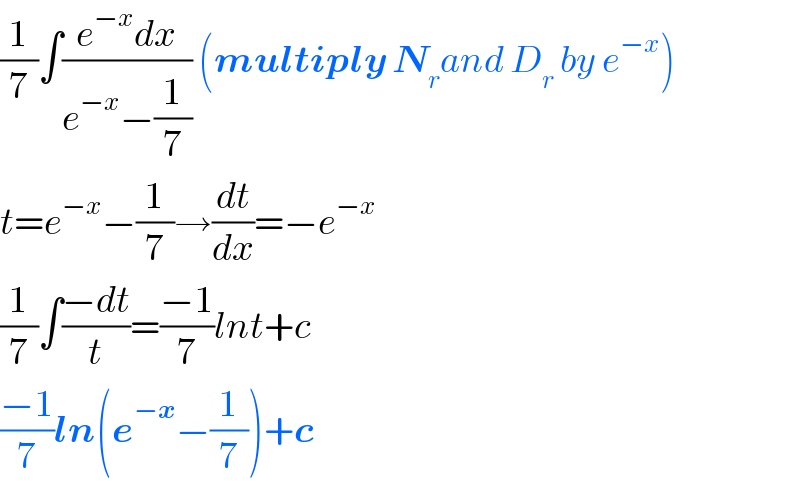
$$\frac{\mathrm{1}}{\mathrm{7}}\int\frac{{e}^{−{x}} {dx}}{{e}^{−{x}} −\frac{\mathrm{1}}{\mathrm{7}}}\:\left(\boldsymbol{{multiply}}\:\boldsymbol{{N}}_{{r}} {and}\:{D}_{{r}} \:{by}\:{e}^{−{x}} \right) \\ $$$${t}={e}^{−{x}} −\frac{\mathrm{1}}{\mathrm{7}}\rightarrow\frac{{dt}}{{dx}}=−{e}^{−{x}} \\ $$$$\frac{\mathrm{1}}{\mathrm{7}}\int\frac{−{dt}}{{t}}=\frac{−\mathrm{1}}{\mathrm{7}}{lnt}+{c} \\ $$$$\frac{−\mathrm{1}}{\mathrm{7}}\boldsymbol{{ln}}\left(\boldsymbol{{e}}^{−\boldsymbol{{x}}} −\frac{\mathrm{1}}{\mathrm{7}}\right)+\boldsymbol{{c}} \\ $$
Commented by sakeefhasan05@gmail.com last updated on 25/Mar/20

$$\mathrm{thank}\:\mathrm{u}\:\mathrm{very}\:\mathrm{much} \\ $$
