Question Number 157057 by amin96 last updated on 19/Oct/21
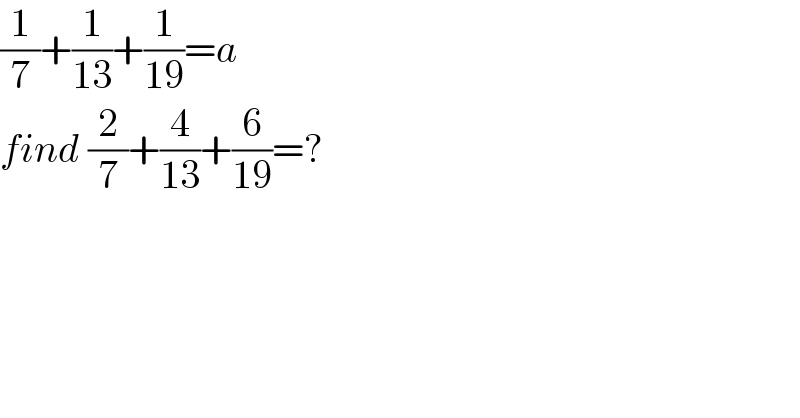
$$\frac{\mathrm{1}}{\mathrm{7}}+\frac{\mathrm{1}}{\mathrm{13}}+\frac{\mathrm{1}}{\mathrm{19}}={a} \\ $$$${find}\:\frac{\mathrm{2}}{\mathrm{7}}+\frac{\mathrm{4}}{\mathrm{13}}+\frac{\mathrm{6}}{\mathrm{19}}=? \\ $$
Commented by aliyn last updated on 19/Oct/21
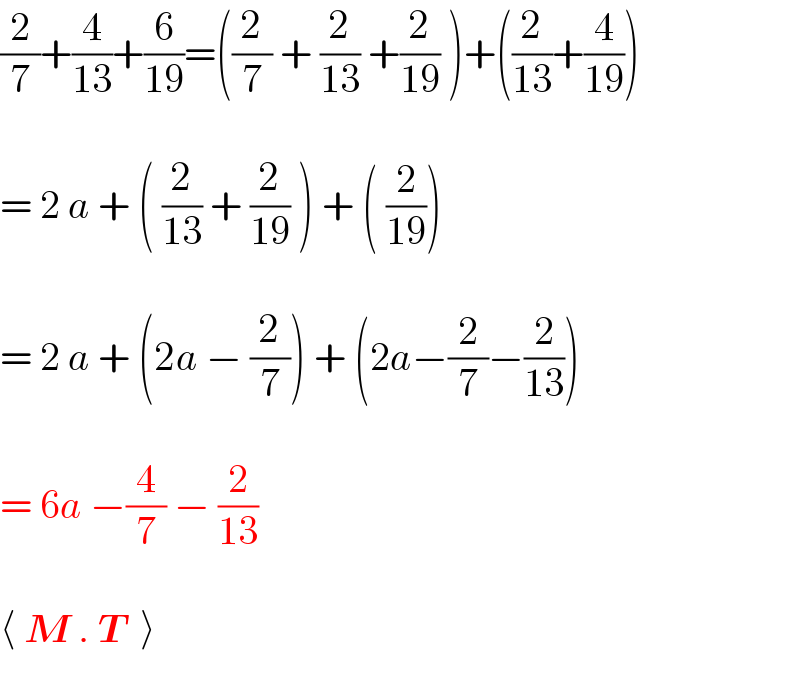
$$\frac{\mathrm{2}}{\mathrm{7}}+\frac{\mathrm{4}}{\mathrm{13}}+\frac{\mathrm{6}}{\mathrm{19}}=\left(\frac{\mathrm{2}}{\mathrm{7}}\:+\:\frac{\mathrm{2}}{\mathrm{13}}\:+\frac{\mathrm{2}}{\mathrm{19}}\:\right)+\left(\frac{\mathrm{2}}{\mathrm{13}}+\frac{\mathrm{4}}{\mathrm{19}}\right) \\ $$$$ \\ $$$$=\:\mathrm{2}\:{a}\:+\:\left(\:\frac{\mathrm{2}}{\mathrm{13}}\:+\:\frac{\mathrm{2}}{\mathrm{19}}\:\right)\:+\:\left(\:\frac{\mathrm{2}}{\mathrm{19}}\right) \\ $$$$ \\ $$$$=\:\mathrm{2}\:{a}\:+\:\left(\mathrm{2}{a}\:−\:\frac{\mathrm{2}}{\mathrm{7}}\right)\:+\:\left(\mathrm{2}{a}−\frac{\mathrm{2}}{\mathrm{7}}−\frac{\mathrm{2}}{\mathrm{13}}\right) \\ $$$$ \\ $$$$=\:\mathrm{6}{a}\:−\frac{\mathrm{4}}{\mathrm{7}}\:−\:\frac{\mathrm{2}}{\mathrm{13}} \\ $$$$ \\ $$$$\langle\:\boldsymbol{{M}}\:.\:\boldsymbol{{T}}\:\:\rangle \\ $$
Commented by mr W last updated on 19/Oct/21
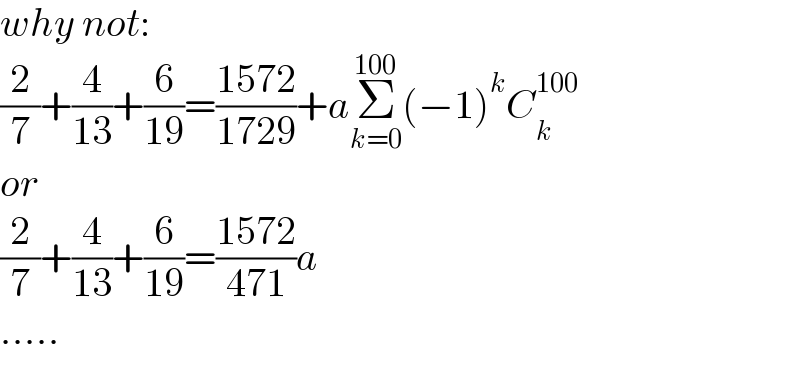
$${why}\:{not}: \\ $$$$\frac{\mathrm{2}}{\mathrm{7}}+\frac{\mathrm{4}}{\mathrm{13}}+\frac{\mathrm{6}}{\mathrm{19}}=\frac{\mathrm{1572}}{\mathrm{1729}}+{a}\underset{{k}=\mathrm{0}} {\overset{\mathrm{100}} {\sum}}\left(−\mathrm{1}\right)^{{k}} {C}_{{k}} ^{\mathrm{100}} \\ $$$${or} \\ $$$$\frac{\mathrm{2}}{\mathrm{7}}+\frac{\mathrm{4}}{\mathrm{13}}+\frac{\mathrm{6}}{\mathrm{19}}=\frac{\mathrm{1572}}{\mathrm{471}}{a} \\ $$$$….. \\ $$
Answered by apriadodir last updated on 19/Oct/21
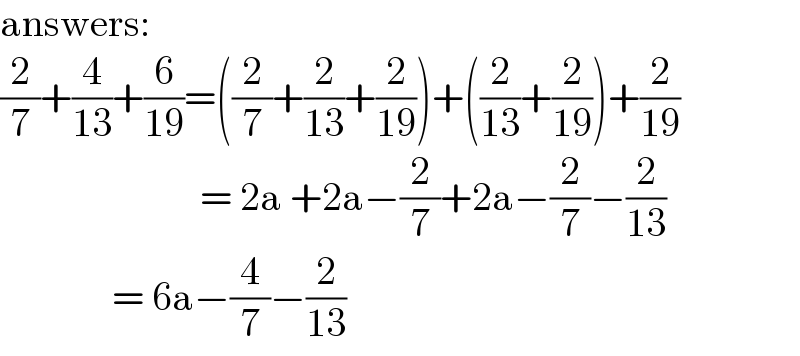
$$\mathrm{answers}: \\ $$$$\frac{\mathrm{2}}{\mathrm{7}}+\frac{\mathrm{4}}{\mathrm{13}}+\frac{\mathrm{6}}{\mathrm{19}}=\left(\frac{\mathrm{2}}{\mathrm{7}}+\frac{\mathrm{2}}{\mathrm{13}}+\frac{\mathrm{2}}{\mathrm{19}}\right)+\left(\frac{\mathrm{2}}{\mathrm{13}}+\frac{\mathrm{2}}{\mathrm{19}}\right)+\frac{\mathrm{2}}{\mathrm{19}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{2a}\:+\mathrm{2a}−\frac{\mathrm{2}}{\mathrm{7}}+\mathrm{2a}−\frac{\mathrm{2}}{\mathrm{7}}−\frac{\mathrm{2}}{\mathrm{13}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{6a}−\frac{\mathrm{4}}{\mathrm{7}}−\frac{\mathrm{2}}{\mathrm{13}} \\ $$
