Question Number 13725 by prakash jain last updated on 22/May/17
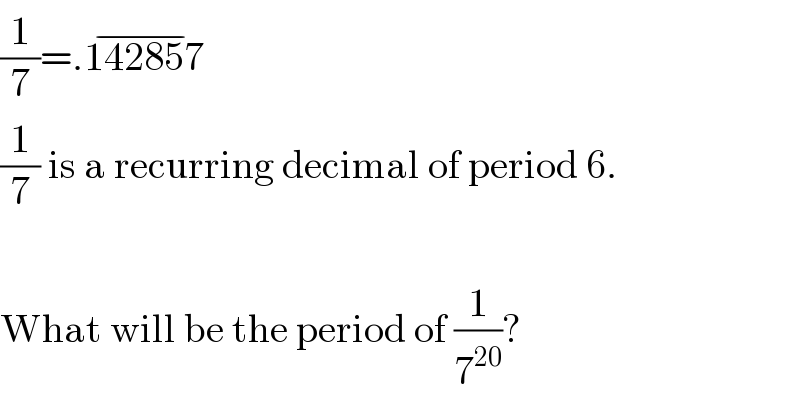
$$\frac{\mathrm{1}}{\mathrm{7}}=.\overline {\mathrm{142857}} \\ $$$$\frac{\mathrm{1}}{\mathrm{7}}\:\mathrm{is}\:\mathrm{a}\:\mathrm{recurring}\:\mathrm{decimal}\:\mathrm{of}\:\mathrm{period}\:\mathrm{6}. \\ $$$$ \\ $$$$\mathrm{What}\:\mathrm{will}\:\mathrm{be}\:\mathrm{the}\:\mathrm{period}\:\mathrm{of}\:\frac{\mathrm{1}}{\mathrm{7}^{\mathrm{20}} }? \\ $$
Commented by RasheedSoomro last updated on 12/Jun/17
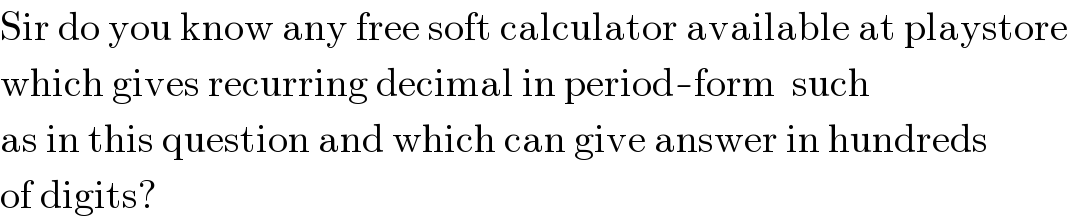
$$\mathrm{Sir}\:\mathrm{do}\:\mathrm{you}\:\mathrm{know}\:\mathrm{any}\:\mathrm{free}\:\mathrm{soft}\:\mathrm{calculator}\:\mathrm{available}\:\mathrm{at}\:\mathrm{playstore} \\ $$$$\mathrm{which}\:\mathrm{gives}\:\mathrm{recurring}\:\mathrm{decimal}\:\mathrm{in}\:\mathrm{period}-\mathrm{form}\:\:\mathrm{such} \\ $$$$\mathrm{as}\:\mathrm{in}\:\mathrm{this}\:\mathrm{question}\:\mathrm{and}\:\mathrm{which}\:\mathrm{can}\:\mathrm{give}\:\mathrm{answer}\:\mathrm{in}\:\mathrm{hundreds} \\ $$$$\mathrm{of}\:\mathrm{digits}? \\ $$
Commented by prakash jain last updated on 12/Jun/17
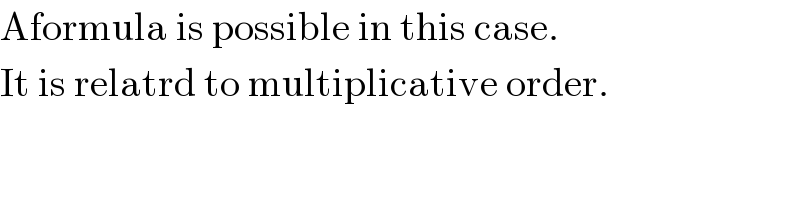
$$\mathrm{Aformula}\:\mathrm{is}\:\mathrm{possible}\:\mathrm{in}\:\mathrm{this}\:\mathrm{case}. \\ $$$$\mathrm{It}\:\mathrm{is}\:\mathrm{relatrd}\:\mathrm{to}\:\mathrm{multiplicative}\:\mathrm{order}. \\ $$
