Question Number 27003 by Joel578 last updated on 01/Jan/18
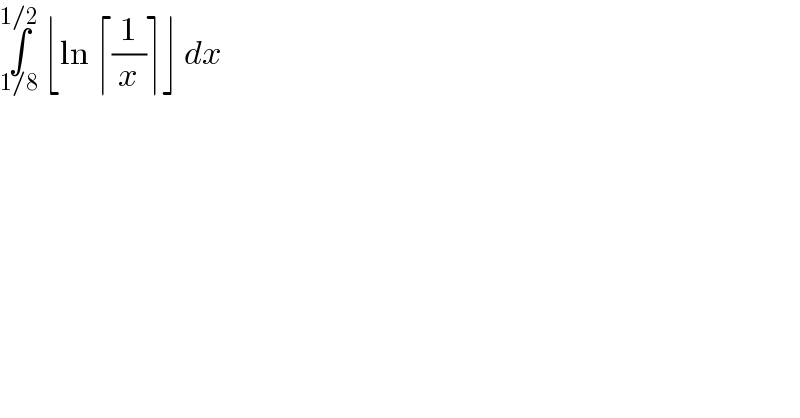
$$\underset{\mathrm{1}/\mathrm{8}} {\overset{\mathrm{1}/\mathrm{2}} {\int}}\:\lfloor\mathrm{ln}\:\lceil\frac{\mathrm{1}}{{x}}\rceil\rfloor\:{dx} \\ $$
Commented by abdo imad last updated on 01/Jan/18
![if you mean the integral I= ∫_(1/8) ^(1/2) ln[ (1/x)]dx we do the changement (1/x)=t⇒I= − ∫_8 ^2 ln[t](dt/t^2 )= ∫_2 ^8 ((ln([t]))/t^2 )dt =Σ_(k=2) ^7 ∫_k ^(k+1) ((lnk)/t^2 )dt = Σ_(k=2) ^(k=7) ln(k)[−(1/t)]_k ^(k+1) = Σ_(k=2) ^(k=7) ( (1/k) −(1/(k+1)) )ln(k) = Σ_(k=2) ^7 ((ln(k))/(k(k+1))) = ((ln(2))/6) +((ln(3))/(12)) +((ln(4))/(20)) + ((ln(5))/(30)) +((ln(6))/(42)) +((ln(7))/(56)).](https://www.tinkutara.com/question/Q27039.png)
$$\:{if}\:{you}\:{mean}\:{the}\:{integral}\:{I}=\:\int_{\frac{\mathrm{1}}{\mathrm{8}}} ^{\frac{\mathrm{1}}{\mathrm{2}}} {ln}\left[\:\frac{\mathrm{1}}{{x}}\right]{dx}\:{we}\:{do}\:{the}\:{changement} \\ $$$$\frac{\mathrm{1}}{{x}}={t}\Rightarrow{I}=\:−\:\int_{\mathrm{8}} ^{\mathrm{2}} {ln}\left[{t}\right]\frac{{dt}}{{t}^{\mathrm{2}} }=\:\int_{\mathrm{2}} ^{\mathrm{8}} \frac{{ln}\left(\left[{t}\right]\right)}{{t}^{\mathrm{2}} }{dt}\:=\sum_{{k}=\mathrm{2}} ^{\mathrm{7}} \int_{{k}} ^{{k}+\mathrm{1}} \:\frac{{lnk}}{{t}^{\mathrm{2}} }{dt} \\ $$$$=\:\sum_{{k}=\mathrm{2}} ^{{k}=\mathrm{7}} {ln}\left({k}\right)\left[−\frac{\mathrm{1}}{{t}}\right]_{{k}} ^{{k}+\mathrm{1}} =\:\sum_{{k}=\mathrm{2}} ^{{k}=\mathrm{7}} \left(\:\frac{\mathrm{1}}{{k}}\:−\frac{\mathrm{1}}{{k}+\mathrm{1}}\:\right){ln}\left({k}\right) \\ $$$$=\:\sum_{{k}=\mathrm{2}} ^{\mathrm{7}} \frac{{ln}\left({k}\right)}{{k}\left({k}+\mathrm{1}\right)}\:=\:\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{6}}\:+\frac{{ln}\left(\mathrm{3}\right)}{\mathrm{12}}\:+\frac{{ln}\left(\mathrm{4}\right)}{\mathrm{20}}\:+\:\frac{{ln}\left(\mathrm{5}\right)}{\mathrm{30}}\:+\frac{{ln}\left(\mathrm{6}\right)}{\mathrm{42}}\:+\frac{{ln}\left(\mathrm{7}\right)}{\mathrm{56}}. \\ $$
Commented by Joel578 last updated on 02/Jan/18
$${thank}\:{you}\:{very}\:{much} \\ $$
