Question Number 129269 by bramlexs22 last updated on 14/Jan/21
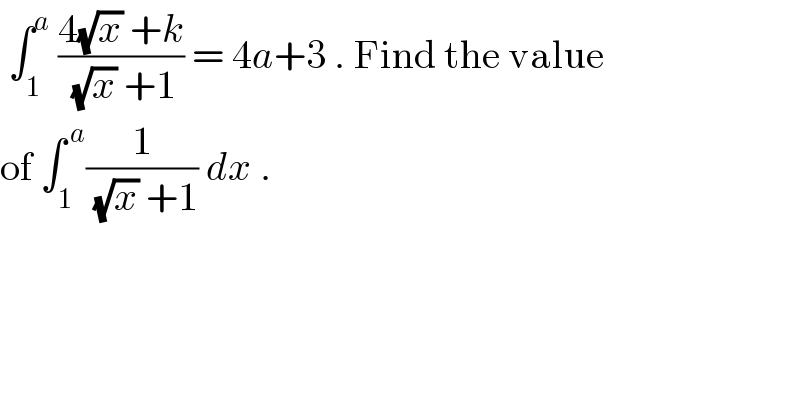
$$\:\int_{\mathrm{1}} ^{{a}} \:\frac{\mathrm{4}\sqrt{{x}}\:+{k}}{\:\sqrt{{x}}\:+\mathrm{1}}\:=\:\mathrm{4}{a}+\mathrm{3}\:.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{value} \\ $$$$\mathrm{of}\:\int_{\mathrm{1}} ^{\:{a}} \frac{\mathrm{1}}{\:\sqrt{{x}}\:+\mathrm{1}}\:{dx}\:. \\ $$
Answered by liberty last updated on 14/Jan/21
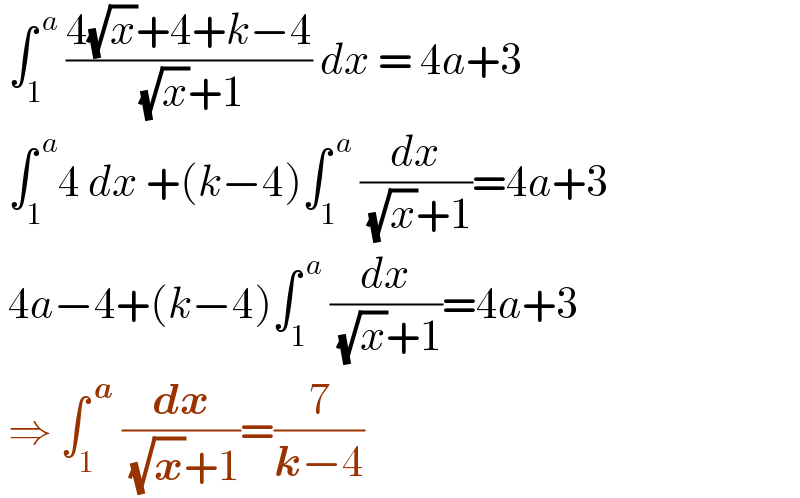
$$\:\int_{\mathrm{1}} ^{\:{a}} \:\frac{\mathrm{4}\sqrt{{x}}+\mathrm{4}+{k}−\mathrm{4}}{\:\sqrt{{x}}+\mathrm{1}}\:{dx}\:=\:\mathrm{4}{a}+\mathrm{3} \\ $$$$\:\int_{\mathrm{1}} ^{\:{a}} \mathrm{4}\:{dx}\:+\left({k}−\mathrm{4}\right)\int_{\mathrm{1}} ^{\:{a}} \:\frac{{dx}}{\:\sqrt{{x}}+\mathrm{1}}=\mathrm{4}{a}+\mathrm{3} \\ $$$$\:\mathrm{4}{a}−\mathrm{4}+\left({k}−\mathrm{4}\right)\int_{\mathrm{1}} ^{\:{a}} \:\frac{{dx}}{\:\sqrt{{x}}+\mathrm{1}}=\mathrm{4}{a}+\mathrm{3} \\ $$$$\:\Rightarrow\:\int_{\mathrm{1}} ^{\:\boldsymbol{{a}}} \:\frac{\boldsymbol{{dx}}}{\:\sqrt{\boldsymbol{{x}}}+\mathrm{1}}=\frac{\mathrm{7}}{\boldsymbol{{k}}−\mathrm{4}}\: \\ $$
