1-ae-a-1-x-a-1-e-ax-x-2-dx-a-z-

Question Number 83385 by M±th+et£s last updated on 01/Mar/20

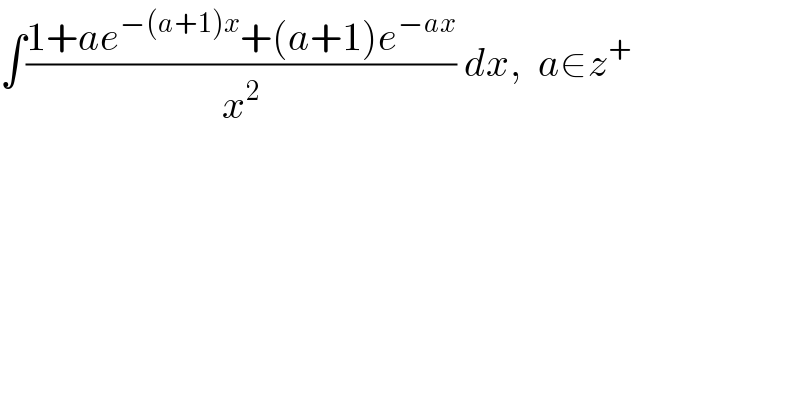
$$\int\frac{\mathrm{1}+{ae}^{−\left({a}+\mathrm{1}\right){x}} +\left({a}+\mathrm{1}\right){e}^{−{ax}} }{{x}^{\mathrm{2}} }\:{dx},\:\:{a}\in{z}^{+} \\ $$

Commented by M±th+et£s last updated on 01/Mar/20

$${typo}\: \\ $$$$\int_{\mathrm{0}} ^{\infty} \\ $$

Answered by mind is power last updated on 01/Mar/20

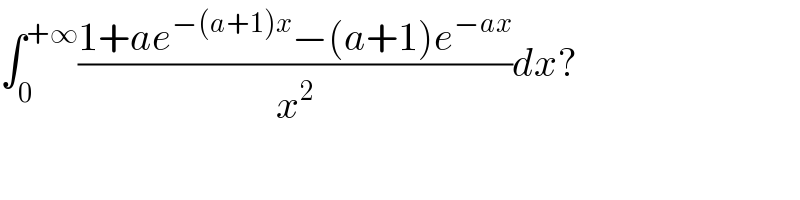
∫_0 ^(+∞) ((1+ae^(−(a+1)x) −(a+1)e^(−ax) )/x^2 )dx?

$$\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{1}+{ae}^{−\left({a}+\mathrm{1}\right){x}} −\left({a}+\mathrm{1}\right){e}^{−{ax}} }{{x}^{\mathrm{2}} }{dx}? \\ $$

Commented by M±th+et£s last updated on 01/Mar/20

$${yes}\:{sir} \\ $$

Commented by mathmax by abdo last updated on 02/Mar/20

by parts u^′ =(1/x^2 ) and v=1+ae^(−(a+1)x) −(a+1)e^(−ax) ⇒ I=[−(1/x)(1+ae^(−(a+1)x) −(a+1)e^(−ax) )]_0 ^(+∞) + ∫_0 ^∞ (e^(−(a+1)x) −a(a+1)e^(−(a+1)x) −e^(−ax) +a(a+1)e^(−ax) )(dx/x) =∫_0 ^∞ ((e^(−(a+1)x) −e^(−ax) )/x)dx −a(a+1)∫_0 ^∞ ((e^(−(a+1)x) −e^(−ax) )/x)dx =(1−a^2 −a)∫_0 ^∞ ((e^(−(a+1)x) −e^(−ax) )/x)dx let ξ(a)=∫_0 ^∞ ((e^(−(a+1)x) −e^(−ax) )/x)dx ⇒ξ^′ (a) =∫_0 ^∞ ((−x e^(−(a+1)x) +xe^(−ax) )/x)dx =∫_0 ^∞ e^(−ax) dx−∫_0 ^∞ e^(−(a+1)x) dx =[−(e^(−ax) /a)]_0 ^∞ −[−(e^(−(a+1)x) /(a+1))]_0 ^(+∞) =(1/a)−(1/(a+1)) ⇒ξ(a) =ln((a/(a+1)))+c (we supoose a>0 ) lim_(a→+∞) ξ(a)=0=c ⇒ξ(a)=ln((a/(a+1))) ⇒I =(1−a^2 −a)ln((a/(a+1))) rest to prove that lim_(x→0) ((1+ae^(−(a+1)x) −(a+1)e^(−ax) )/x) =0 e^(−(a+1)x) ∼1−(a+1)x+(((a+1)x^2 )/2)⇒a e^(−(a+1)x) ∼a−a(a+1)x+((a(a+1)x^2 )/2) e^(−ax) ∼1−ax+((a^2 x^2 )/2) ⇒(a+1)e^(−ax) ∼a+1−a(a+1)x +((a^2 (a+1)x^2 )/2) ⇒ (...−(....)∼1+a−a(a+1)x+((a(a+1)x^2 )/2)−a−1−a(a+1)x−((a^2 (a+1)x^2 )/2) =((a+1)/2)(a−a^2 )x^2 ⇒(((...)−(...))/x)∼ (((a+1)(a−a^2 )x)/2)→0 (x→0)

$${by}\:{parts}\:{u}^{'} =\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:{and}\:{v}=\mathrm{1}+{ae}^{−\left({a}+\mathrm{1}\right){x}} −\left({a}+\mathrm{1}\right){e}^{−{ax}} \:\Rightarrow \\ $$$${I}=\left[−\frac{\mathrm{1}}{{x}}\left(\mathrm{1}+{ae}^{−\left({a}+\mathrm{1}\right){x}} −\left({a}+\mathrm{1}\right){e}^{−{ax}} \right)\right]_{\mathrm{0}} ^{+\infty} + \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\left({e}^{−\left({a}+\mathrm{1}\right){x}} \:−{a}\left({a}+\mathrm{1}\right){e}^{−\left({a}+\mathrm{1}\right){x}} −{e}^{−{ax}} +{a}\left({a}+\mathrm{1}\right){e}^{−{ax}} \right)\frac{{dx}}{{x}} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{−\left({a}+\mathrm{1}\right){x}} −{e}^{−{ax}} }{{x}}{dx}\:−{a}\left({a}+\mathrm{1}\right)\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−\left({a}+\mathrm{1}\right){x}} −{e}^{−{ax}} }{{x}}{dx} \\ $$$$=\left(\mathrm{1}−{a}^{\mathrm{2}} −{a}\right)\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{−\left({a}+\mathrm{1}\right){x}} −{e}^{−{ax}} }{{x}}{dx}\:{let}\:\xi\left({a}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−\left({a}+\mathrm{1}\right){x}} −{e}^{−{ax}} }{{x}}{dx} \\ $$$$\Rightarrow\xi^{'} \left({a}\right)\:=\int_{\mathrm{0}} ^{\infty} \frac{−{x}\:{e}^{−\left({a}+\mathrm{1}\right){x}} +{xe}^{−{ax}} }{{x}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:{e}^{−{ax}} {dx}−\int_{\mathrm{0}} ^{\infty} \:{e}^{−\left({a}+\mathrm{1}\right){x}} \:{dx}\:=\left[−\frac{{e}^{−{ax}} }{{a}}\right]_{\mathrm{0}} ^{\infty} −\left[−\frac{{e}^{−\left({a}+\mathrm{1}\right){x}} }{{a}+\mathrm{1}}\right]_{\mathrm{0}} ^{+\infty} \\ $$$$=\frac{\mathrm{1}}{{a}}−\frac{\mathrm{1}}{{a}+\mathrm{1}}\:\Rightarrow\xi\left({a}\right)\:={ln}\left(\frac{{a}}{{a}+\mathrm{1}}\right)+{c}\:\:\:\:\:\left({we}\:{supoose}\:{a}>\mathrm{0}\:\right) \\ $$$${lim}_{{a}\rightarrow+\infty} \xi\left({a}\right)=\mathrm{0}={c}\:\Rightarrow\xi\left({a}\right)={ln}\left(\frac{{a}}{{a}+\mathrm{1}}\right)\:\Rightarrow{I}\:=\left(\mathrm{1}−{a}^{\mathrm{2}} −{a}\right){ln}\left(\frac{{a}}{{a}+\mathrm{1}}\right) \\ $$$${rest}\:{to}\:{prove}\:{that}\:{lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\:\:\frac{\mathrm{1}+{ae}^{−\left({a}+\mathrm{1}\right){x}} −\left({a}+\mathrm{1}\right){e}^{−{ax}} }{{x}}\:=\mathrm{0} \\ $$$${e}^{−\left({a}+\mathrm{1}\right){x}} \sim\mathrm{1}−\left({a}+\mathrm{1}\right){x}+\frac{\left({a}+\mathrm{1}\right){x}^{\mathrm{2}} }{\mathrm{2}}\Rightarrow{a}\:{e}^{−\left({a}+\mathrm{1}\right){x}} \sim{a}−{a}\left({a}+\mathrm{1}\right){x}+\frac{{a}\left({a}+\mathrm{1}\right){x}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${e}^{−{ax}} \:\sim\mathrm{1}−{ax}+\frac{{a}^{\mathrm{2}} {x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow\left({a}+\mathrm{1}\right){e}^{−{ax}} \:\sim{a}+\mathrm{1}−{a}\left({a}+\mathrm{1}\right){x}\:+\frac{{a}^{\mathrm{2}} \left({a}+\mathrm{1}\right){x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow \\ $$$$\left(…−\left(….\right)\sim\mathrm{1}+{a}−{a}\left({a}+\mathrm{1}\right){x}+\frac{{a}\left({a}+\mathrm{1}\right){x}^{\mathrm{2}} }{\mathrm{2}}−{a}−\mathrm{1}−{a}\left({a}+\mathrm{1}\right){x}−\frac{{a}^{\mathrm{2}} \left({a}+\mathrm{1}\right){x}^{\mathrm{2}} }{\mathrm{2}}\right. \\ $$$$=\frac{{a}+\mathrm{1}}{\mathrm{2}}\left({a}−{a}^{\mathrm{2}} \right){x}^{\mathrm{2}} \:\Rightarrow\frac{\left(…\right)−\left(…\right)}{{x}}\sim\:\frac{\left({a}+\mathrm{1}\right)\left({a}−{a}^{\mathrm{2}} \right){x}}{\mathrm{2}}\rightarrow\mathrm{0}\:\left({x}\rightarrow\mathrm{0}\right) \\ $$

Answered by mind is power last updated on 02/Mar/20

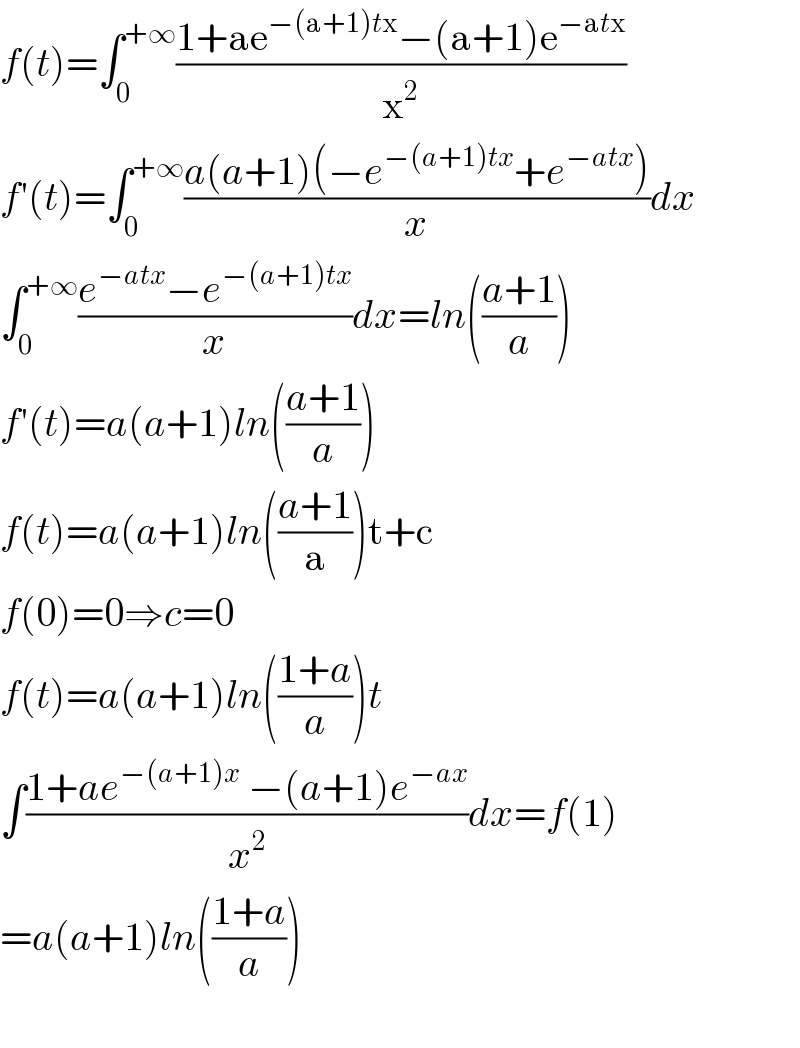
f(t)=∫_0 ^(+∞) ((1+ae^(−(a+1)tx) −(a+1)e^(−atx) )/x^2 ) f′(t)=∫_0 ^(+∞) ((a(a+1)(−e^(−(a+1)tx) +e^(−atx) ))/x)dx ∫_0 ^(+∞) ((e^(−atx) −e^(−(a+1)tx) )/x)dx=ln(((a+1)/a)) f′(t)=a(a+1)ln(((a+1)/a)) f(t)=a(a+1)ln(((a+1)/a))t+c f(0)=0⇒c=0 f(t)=a(a+1)ln(((1+a)/a))t ∫((1+ae^(−(a+1)x) −(a+1)e^(−ax) )/x^2 )dx=f(1) =a(a+1)ln(((1+a)/a))

$${f}\left({t}\right)=\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{1}+\mathrm{ae}^{−\left(\mathrm{a}+\mathrm{1}\right){t}\mathrm{x}} −\left(\mathrm{a}+\mathrm{1}\right)\mathrm{e}^{−\mathrm{a}{t}\mathrm{x}} }{\mathrm{x}^{\mathrm{2}} } \\ $$$${f}'\left({t}\right)=\int_{\mathrm{0}} ^{+\infty} \frac{{a}\left({a}+\mathrm{1}\right)\left(−{e}^{−\left({a}+\mathrm{1}\right){tx}} +{e}^{−{atx}} \right)}{{x}}{dx} \\ $$$$\int_{\mathrm{0}} ^{+\infty} \frac{{e}^{−{atx}} −{e}^{−\left({a}+\mathrm{1}\right){tx}} }{{x}}{dx}={ln}\left(\frac{{a}+\mathrm{1}}{{a}}\right) \\ $$$${f}'\left({t}\right)={a}\left({a}+\mathrm{1}\right){ln}\left(\frac{{a}+\mathrm{1}}{{a}}\right) \\ $$$${f}\left({t}\right)={a}\left({a}+\mathrm{1}\right){ln}\left(\frac{{a}+\mathrm{1}}{\mathrm{a}}\right)\mathrm{t}+\mathrm{c} \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{0}\Rightarrow{c}=\mathrm{0} \\ $$$${f}\left({t}\right)={a}\left({a}+\mathrm{1}\right){ln}\left(\frac{\mathrm{1}+{a}}{{a}}\right){t} \\ $$$$\int\frac{\mathrm{1}+{ae}^{−\left({a}+\mathrm{1}\right){x}} \:−\left({a}+\mathrm{1}\right){e}^{−{ax}} }{{x}^{\mathrm{2}} }{dx}={f}\left(\mathrm{1}\right) \\ $$$$={a}\left({a}+\mathrm{1}\right){ln}\left(\frac{\mathrm{1}+{a}}{{a}}\right) \\ $$$$ \\ $$

Commented by mind is power last updated on 02/Mar/20

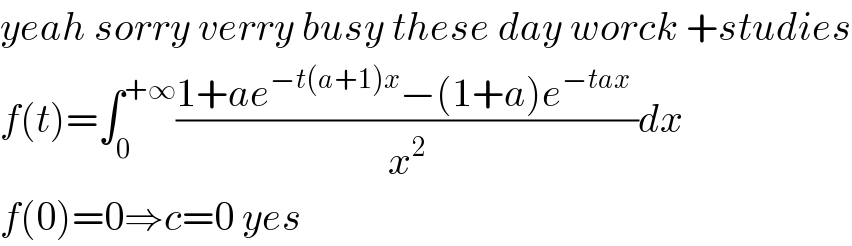
yeah sorry verry busy these day worck +studies f(t)=∫_0 ^(+∞) ((1+ae^(−t(a+1)x) −(1+a)e^(−tax) )/x^2 )dx f(0)=0⇒c=0 yes

$${yeah}\:{sorry}\:{verry}\:{busy}\:{these}\:{day}\:{worck}\:+{studies} \\ $$$${f}\left({t}\right)=\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{1}+{ae}^{−{t}\left({a}+\mathrm{1}\right){x}} −\left(\mathrm{1}+{a}\right){e}^{−{tax}} \:}{{x}^{\mathrm{2}} }{dx} \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{0}\Rightarrow{c}=\mathrm{0}\:{yes} \\ $$

Commented by M±th+et£s last updated on 02/Mar/20