Question Number 49953 by maxmathsup by imad last updated on 12/Dec/18
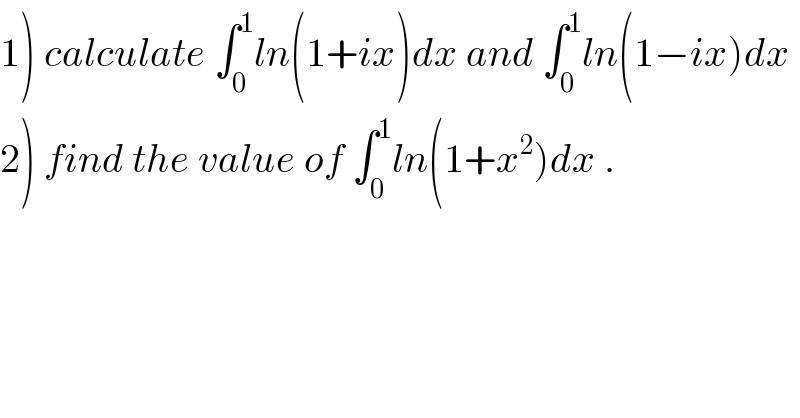
$$\left.\mathrm{1}\right)\:{calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{ix}\right){dx}\:{and}\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}−{ix}\right){dx} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){dx}\:. \\ $$
Commented by Abdo msup. last updated on 14/Dec/18
![1) we have 1+ix =(√(1+x^2 ))((1/( (√(1+x^2 )))) +i(x/( (√(1+x^2 ))))) =(√(1+x^2 ))e^(iarctan(x)) ⇒∫_0 ^1 ln(1+ix)dx =(1/2) ∫_0 ^1 ln(1+x^2 )dx +i ∫_0 ^1 arctanxdx but ∫_0 ^1 ln(1+x^2 )dx =_(by parts) [xln(1+x^2 )]_0 ^1 −∫_0 ^1 x ((2x)/(1+x^2 ))dx =ln(2) −2 ∫_0 ^1 ((1+x^2 −1)/(1+x^2 ))dx=ln(2)−2 +2 ∫_0 ^1 (dx/(1+x^2 )) =ln(2)−2 +2.(π/4) =ln(2)−2+(π/2) also by parts ∫_0 ^1 arctan(x)dx = [x arctanx]_0 ^1 −∫_0 ^1 (x/(1+x^2 ))dx =(π/4) −[(1/2)ln(1+x^2 )]_0 ^1 =(π/4) −(1/2)ln(2) ⇒ ∫_0 ^1 ln(1+ix)dx =((ln(2))/2) −1+(π/4) +i((π/4) −(1/2)ln(2))](https://www.tinkutara.com/question/Q50130.png)
$$\left.\mathrm{1}\right)\:{we}\:{have}\:\mathrm{1}+{ix}\:=\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:+{i}\frac{{x}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right)\:=\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }{e}^{{iarctan}\left({x}\right)} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{ix}\right){dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){dx}\:+{i}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{arctanxdx}\:{but} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){dx}\:=_{{by}\:{parts}} \:\:\left[{xln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:−\int_{\mathrm{0}} ^{\mathrm{1}} {x}\:\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$={ln}\left(\mathrm{2}\right)\:−\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}+{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}={ln}\left(\mathrm{2}\right)−\mathrm{2}\:+\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$={ln}\left(\mathrm{2}\right)−\mathrm{2}\:+\mathrm{2}.\frac{\pi}{\mathrm{4}}\:={ln}\left(\mathrm{2}\right)−\mathrm{2}+\frac{\pi}{\mathrm{2}}\:\:{also}\:{by}\:{parts} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{arctan}\left({x}\right){dx}\:=\:\left[{x}\:{arctanx}\right]_{\mathrm{0}} ^{\mathrm{1}} \:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$=\frac{\pi}{\mathrm{4}}\:−\left[\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\frac{\pi}{\mathrm{4}}\:−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{2}\right)\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{ln}\left(\mathrm{1}+{ix}\right){dx}\:=\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}}\:−\mathrm{1}+\frac{\pi}{\mathrm{4}}\:+{i}\left(\frac{\pi}{\mathrm{4}}\:−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{2}\right)\right) \\ $$
Commented by Abdo msup. last updated on 14/Dec/18
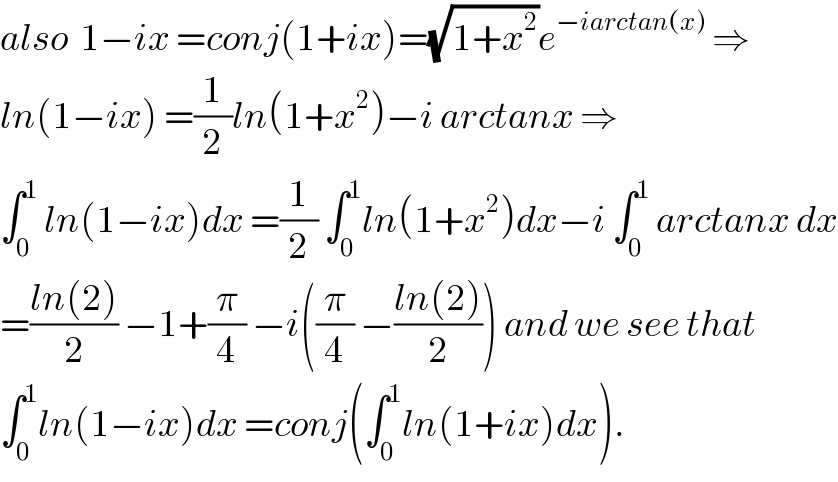
$${also}\:\:\mathrm{1}−{ix}\:={conj}\left(\mathrm{1}+{ix}\right)=\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }{e}^{−{iarctan}\left({x}\right)} \:\Rightarrow \\ $$$${ln}\left(\mathrm{1}−{ix}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)−{i}\:{arctanx}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{ln}\left(\mathrm{1}−{ix}\right){dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){dx}−{i}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{arctanx}\:{dx} \\ $$$$=\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}}\:−\mathrm{1}+\frac{\pi}{\mathrm{4}}\:−{i}\left(\frac{\pi}{\mathrm{4}}\:−\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}}\right)\:{and}\:{we}\:{see}\:{that} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}−{ix}\right){dx}\:={conj}\left(\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{ix}\right){dx}\right). \\ $$
Commented by Abdo msup. last updated on 14/Dec/18
![2) by parts ∫_0 ^1 ln(1+x^2 )dx =[xln(1+x^2 )]_0 ^1 −∫_0 ^1 x ((2x)/(1+x^2 ))dx =ln(2)−2 ∫_0 ^1 ((1+x^2 −1)/(1+x^2 ))dx =ln(2)−2 +2 ∫_0 ^1 (dx/(1+x^2 )) =ln(2)−2 +2.(π/4) =ln(2)−2 +(π/2) complex method ∫_0 ^1 ln(1+x^2 )dx =∫_0 ^1 ln(1+ix)(1−ix))dx =∫_0 ^1 ln(1+ix)dx +∫_0 ^1 ln(1−ix)dx =((ln(2))/2) −1 +(π/4) +((ln(2))/2) −1+(π/4) =ln(2)−2 +(π/2) .](https://www.tinkutara.com/question/Q50133.png)
$$\left.\mathrm{2}\right)\:{by}\:{parts}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){dx}\:=\left[{xln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:−\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}\:\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$={ln}\left(\mathrm{2}\right)−\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{1}+{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:={ln}\left(\mathrm{2}\right)−\mathrm{2}\:+\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$={ln}\left(\mathrm{2}\right)−\mathrm{2}\:+\mathrm{2}.\frac{\pi}{\mathrm{4}}\:={ln}\left(\mathrm{2}\right)−\mathrm{2}\:+\frac{\pi}{\mathrm{2}} \\ $$$${complex}\:{method} \\ $$$$\left.\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{ix}\right)\left(\mathrm{1}−{ix}\right)\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{ix}\right){dx}\:+\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}−{ix}\right){dx} \\ $$$$=\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}}\:−\mathrm{1}\:+\frac{\pi}{\mathrm{4}}\:+\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}}\:−\mathrm{1}+\frac{\pi}{\mathrm{4}}\:={ln}\left(\mathrm{2}\right)−\mathrm{2}\:+\frac{\pi}{\mathrm{2}}\:. \\ $$
