Question Number 96834 by mathmax by abdo last updated on 05/Jun/20
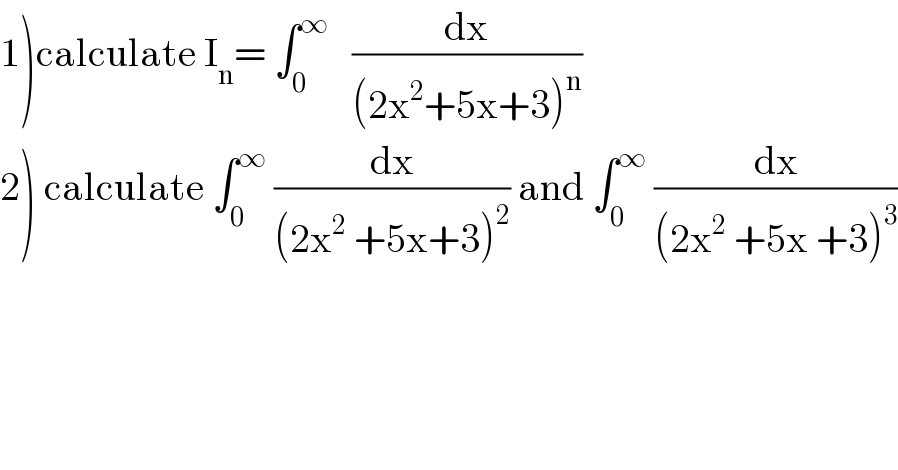
$$\left.\mathrm{1}\right)\mathrm{calculate}\:\mathrm{I}_{\mathrm{n}} =\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{dx}}{\left(\mathrm{2x}^{\mathrm{2}} +\mathrm{5x}+\mathrm{3}\right)^{\mathrm{n}} } \\ $$$$\left.\mathrm{2}\right)\:\mathrm{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{2x}^{\mathrm{2}} \:+\mathrm{5x}+\mathrm{3}\right)^{\mathrm{2}} }\:\mathrm{and}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{2x}^{\mathrm{2}} \:+\mathrm{5x}\:+\mathrm{3}\right)^{\mathrm{3}} } \\ $$
Commented by mathmax by abdo last updated on 05/Jun/20

$$\mathrm{n}\:\mathrm{integr}\:\mathrm{natural} \\ $$
Answered by abdomathmax last updated on 05/Jun/20
![1) 2x^2 +5x+3 =0 →Δ =25−4.2.3 =1 ⇒ x_1 =((−5+1)/4) =−1 and x_2 =((−5−1)/4) =−(3/2) ⇒ 2x^2 +5x +3 =2(x+1)(x+(3/2)) =(x+1)(2x+3) ⇒ I_n =∫_0 ^∞ (dx/((x+1)^n (2x+3)^n )) =∫_0 ^∞ (dx/((((x+1)/(2x+3)))^n (2x+3)^(2n) )) changement ((x+1)/(2x+3)) =t give x+1 =2tx +3t ⇒ (1−2t)x =3t−1 ⇒x =((3t−1)/(1−2t)) ⇒ (dx/dt) = ((3(1−2t)−(3t−1)(−2))/((2t−1)^2 )) =((3−6t+6t−2)/((2t−1)^2 )) =(1/((2t−1)^2 )) also 2x+3 =((6t−2)/(1−2t)) +3 =((6t−2+3−6t)/(1−2t)) =(1/((1−2t))) ⇒ I_n =∫_(1/3) ^(1/2) (dt/((2t−1)^2 t^n ((1/(2t−1)))^(2n) )) =∫_(1/3) ^(1/2) (((2t−1)^(2n−2) )/t^n ) dt =∫_(1/3) ^(1/2) ((Σ_(k=0) ^(2n−2) C_(2n−2) ^k (2t)^k (−1)^(2n−2−k) )/t^n ) dt =Σ_(k=0) ^(2n−2) C_(2n−2) ^k 2^k (−1)^k ∫_(1/3) ^(1/2) t^(k−n) dt =Σ_(k=0 and k≠n−1) ^(2n−2) C_(2n−2) ^k (−2)^k [(1/(k−n+1))t^(k−n+1) ]_(1/3) ^(1/2) + C_(2n−2) ^(n−1) (−2)^(n−1) [ln∣t∣]_(1/3) ^(1/2) I_n =Σ_(k=0 and k≠n−1) ^(2n−2) ((C_(2n−2) ^k (−2)^k )/(k−n+1)){ (1/2^(k−n+1) )−(1/3^(k−n+1) )} +(−2)^(n−1) C_(2n−2) ^(n−1) {ln(3)−ln(2)}](https://www.tinkutara.com/question/Q96973.png)
$$\left.\mathrm{1}\right)\:\mathrm{2x}^{\mathrm{2}} \:+\mathrm{5x}+\mathrm{3}\:=\mathrm{0}\:\rightarrow\Delta\:=\mathrm{25}−\mathrm{4}.\mathrm{2}.\mathrm{3}\:=\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{x}_{\mathrm{1}} =\frac{−\mathrm{5}+\mathrm{1}}{\mathrm{4}}\:=−\mathrm{1}\:\mathrm{and}\:\mathrm{x}_{\mathrm{2}} =\frac{−\mathrm{5}−\mathrm{1}}{\mathrm{4}}\:=−\frac{\mathrm{3}}{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{2x}^{\mathrm{2}} \:+\mathrm{5x}\:+\mathrm{3}\:=\mathrm{2}\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}+\frac{\mathrm{3}}{\mathrm{2}}\right)\:=\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{2x}+\mathrm{3}\right)\:\Rightarrow \\ $$$$\mathrm{I}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dx}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{n}} \left(\mathrm{2x}+\mathrm{3}\right)^{\mathrm{n}} }\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dx}}{\left(\frac{\mathrm{x}+\mathrm{1}}{\mathrm{2x}+\mathrm{3}}\right)^{\mathrm{n}} \left(\mathrm{2x}+\mathrm{3}\right)^{\mathrm{2n}} } \\ $$$$\mathrm{changement}\:\frac{\mathrm{x}+\mathrm{1}}{\mathrm{2x}+\mathrm{3}}\:=\mathrm{t}\:\mathrm{give}\:\mathrm{x}+\mathrm{1}\:=\mathrm{2tx}\:+\mathrm{3t}\:\Rightarrow \\ $$$$\left(\mathrm{1}−\mathrm{2t}\right)\mathrm{x}\:=\mathrm{3t}−\mathrm{1}\:\Rightarrow\mathrm{x}\:=\frac{\mathrm{3t}−\mathrm{1}}{\mathrm{1}−\mathrm{2t}}\:\Rightarrow \\ $$$$\frac{\mathrm{dx}}{\mathrm{dt}}\:=\:\frac{\mathrm{3}\left(\mathrm{1}−\mathrm{2t}\right)−\left(\mathrm{3t}−\mathrm{1}\right)\left(−\mathrm{2}\right)}{\left(\mathrm{2t}−\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\mathrm{3}−\mathrm{6t}+\mathrm{6t}−\mathrm{2}}{\left(\mathrm{2t}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{2t}−\mathrm{1}\right)^{\mathrm{2}} }\:\mathrm{also}\:\mathrm{2x}+\mathrm{3}\:=\frac{\mathrm{6t}−\mathrm{2}}{\mathrm{1}−\mathrm{2t}}\:+\mathrm{3} \\ $$$$=\frac{\mathrm{6t}−\mathrm{2}+\mathrm{3}−\mathrm{6t}}{\mathrm{1}−\mathrm{2t}}\:=\frac{\mathrm{1}}{\left(\mathrm{1}−\mathrm{2t}\right)}\:\Rightarrow \\ $$$$\mathrm{I}_{\mathrm{n}} =\int_{\frac{\mathrm{1}}{\mathrm{3}}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\:\:\frac{\mathrm{dt}}{\left(\mathrm{2t}−\mathrm{1}\right)^{\mathrm{2}} \mathrm{t}^{\mathrm{n}} \left(\frac{\mathrm{1}}{\mathrm{2t}−\mathrm{1}}\right)^{\mathrm{2n}} } \\ $$$$=\int_{\frac{\mathrm{1}}{\mathrm{3}}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\:\:\frac{\left(\mathrm{2t}−\mathrm{1}\right)^{\mathrm{2n}−\mathrm{2}} }{\mathrm{t}^{\mathrm{n}} }\:\mathrm{dt} \\ $$$$=\int_{\frac{\mathrm{1}}{\mathrm{3}}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\:\frac{\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}−\mathrm{2}} \:\mathrm{C}_{\mathrm{2n}−\mathrm{2}} ^{\mathrm{k}} \:\left(\mathrm{2t}\right)^{\mathrm{k}} \left(−\mathrm{1}\right)^{\mathrm{2n}−\mathrm{2}−\mathrm{k}} }{\mathrm{t}^{\mathrm{n}} }\:\mathrm{dt} \\ $$$$=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}−\mathrm{2}} \:\mathrm{C}_{\mathrm{2n}−\mathrm{2}} ^{\mathrm{k}} \:\mathrm{2}^{\mathrm{k}} \left(−\mathrm{1}\right)^{\mathrm{k}} \:\:\int_{\frac{\mathrm{1}}{\mathrm{3}}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\mathrm{t}^{\mathrm{k}−\mathrm{n}} \:\mathrm{dt} \\ $$$$=\sum_{\mathrm{k}=\mathrm{0}\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{k}}\neq\mathrm{n}−\mathrm{1}} ^{\mathrm{2n}−\mathrm{2}} \:\mathrm{C}_{\mathrm{2n}−\mathrm{2}} ^{\mathrm{k}} \:\left(−\mathrm{2}\right)^{\boldsymbol{\mathrm{k}}} \:\left[\frac{\mathrm{1}}{\boldsymbol{\mathrm{k}}−\boldsymbol{\mathrm{n}}+\mathrm{1}}\boldsymbol{\mathrm{t}}^{\boldsymbol{\mathrm{k}}−\boldsymbol{\mathrm{n}}+\mathrm{1}} \right]_{\frac{\mathrm{1}}{\mathrm{3}}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$+\:\mathrm{C}_{\mathrm{2n}−\mathrm{2}} ^{\mathrm{n}−\mathrm{1}} \:\left(−\mathrm{2}\right)^{\mathrm{n}−\mathrm{1}} \left[\mathrm{ln}\mid\mathrm{t}\mid\right]_{\frac{\mathrm{1}}{\mathrm{3}}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\mathrm{I}_{\mathrm{n}} =\sum_{\mathrm{k}=\mathrm{0}\:\mathrm{and}\:\mathrm{k}\neq\mathrm{n}−\mathrm{1}} ^{\mathrm{2n}−\mathrm{2}} \:\frac{\mathrm{C}_{\mathrm{2n}−\mathrm{2}} ^{\mathrm{k}} \:\left(−\mathrm{2}\right)^{\boldsymbol{\mathrm{k}}} }{\boldsymbol{\mathrm{k}}−\boldsymbol{\mathrm{n}}+\mathrm{1}}\left\{\:\frac{\mathrm{1}}{\mathrm{2}^{\boldsymbol{\mathrm{k}}−\boldsymbol{\mathrm{n}}+\mathrm{1}} }−\frac{\mathrm{1}}{\mathrm{3}^{\boldsymbol{\mathrm{k}}−\boldsymbol{\mathrm{n}}+\mathrm{1}} }\right\} \\ $$$$+\left(−\mathrm{2}\right)^{\boldsymbol{\mathrm{n}}−\mathrm{1}} \:\boldsymbol{\mathrm{C}}_{\mathrm{2n}−\mathrm{2}} ^{\mathrm{n}−\mathrm{1}} \:\left\{\mathrm{ln}\left(\mathrm{3}\right)−\mathrm{ln}\left(\mathrm{2}\right)\right\} \\ $$
Commented by abdomathmax last updated on 05/Jun/20

$$\left.\mathrm{2}\right)\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dx}}{\left(\mathrm{2x}^{\mathrm{2}} \:+\mathrm{5x}+\mathrm{3}\right)^{\mathrm{2}} }\:=\mathrm{I}_{\mathrm{2}} \left(\mathrm{n}=\mathrm{2}\right) \\ $$$$=\sum_{\mathrm{k}=\mathrm{0}\:\mathrm{and}\:\mathrm{k}\neq\mathrm{1}} ^{\mathrm{2}} \:\:\frac{\mathrm{C}_{\mathrm{2}} ^{\mathrm{k}} \left(−\mathrm{2}\right)^{\mathrm{k}} }{\mathrm{k}−\mathrm{1}}\left\{\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{k}−\mathrm{1}} }−\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{k}−\mathrm{1}} }\right\} \\ $$$$−\mathrm{2}\:\mathrm{C}_{\mathrm{2}} ^{\mathrm{1}} \mathrm{ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$$$=−\left\{\:\mathrm{2}−\mathrm{3}\right\}\:+\frac{\mathrm{4}}{\mathrm{1}}\left\{\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}\right\}−\mathrm{4ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{5}}{\mathrm{3}}−\mathrm{4ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$
Commented by abdomathmax last updated on 05/Jun/20

$$\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{\mathrm{dx}}{\left(\mathrm{2x}^{\mathrm{2}} \:+\mathrm{5x}\:+\mathrm{3}\right)^{\mathrm{3}} }\:=\mathrm{I}_{\mathrm{3}} \\ $$$$=\sum_{\mathrm{k}=\mathrm{0}\:\mathrm{and}\:\mathrm{k}\neq\mathrm{2}} ^{\mathrm{4}} \:\:\frac{\mathrm{C}_{\mathrm{4}} ^{\mathrm{k}} \:\left(−\mathrm{2}\right)^{\mathrm{k}} }{\mathrm{k}−\mathrm{2}}\left\{\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{k}−\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{k}−\mathrm{2}} }\right\} \\ $$$$+\mathrm{4}\:\mathrm{C}_{\mathrm{4}} ^{\mathrm{2}} \:\mathrm{ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\left\{\mathrm{4}−\mathrm{9}\right\}\:+\frac{\left(−\mathrm{2}\right)\mathrm{C}_{\mathrm{4}} ^{\mathrm{1}} }{−\mathrm{1}}\left\{\mathrm{2}−\mathrm{3}\right\} \\ $$$$−\frac{\mathrm{8C}_{\mathrm{4}} ^{\mathrm{3}} }{\mathrm{1}}\left\{\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}\right\}\:+\frac{\mathrm{16}\:\mathrm{C}_{\mathrm{4}} ^{\mathrm{4}} }{\mathrm{2}}\left\{\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{9}}\right\}+\mathrm{4C}_{\mathrm{4}} ^{\mathrm{2}} \mathrm{ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$$$=… \\ $$
Answered by Sourav mridha last updated on 05/Jun/20
![1)I_n =∫_0 ^∞ (dx/((2x^2 +5x+3)^n )) =(1/2^n )∫_0 ^∞ (dx/((x+(3/2))^n .(x+1)^n )) now let [x+(3/2)]=k(x+1) after some manipulation you get this nice result... =2^(n−1) ∫_1 ^(3/2) (([k−1]^(2(n−1)) )/k^n )dk now I_2 =2∫_1 ^(3/2) (((k−1)^2 )/k^2 )dk=[(5/3)−4ln(3/2)] and I_3 =2^2 ∫_1 ^(3/2) (((k−1)^4 )/k^3 )dk =4∫_1 ^(3/2) ((Σ_(r=0) ^4 C_r ^4 k^((4−r)) (−1)^r )/k^3 )dk =−((525)/(54))+24ln(3/2) ★very lengthy so I avoid the total calculation.](https://www.tinkutara.com/question/Q96975.png)
$$\left.\mathrm{1}\right)\boldsymbol{{I}}_{\boldsymbol{{n}}} =\int_{\mathrm{0}} ^{\infty} \frac{\boldsymbol{{dx}}}{\left(\mathrm{2}\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{5}\boldsymbol{{x}}+\mathrm{3}\right)^{\boldsymbol{{n}}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}^{\boldsymbol{{n}}} }\int_{\mathrm{0}} ^{\infty} \frac{\boldsymbol{{dx}}}{\left(\boldsymbol{{x}}+\frac{\mathrm{3}}{\mathrm{2}}\right)^{\boldsymbol{{n}}} .\left(\boldsymbol{{x}}+\mathrm{1}\right)^{\boldsymbol{{n}}} } \\ $$$$\boldsymbol{{now}}\:\boldsymbol{{let}}\:\left[\boldsymbol{{x}}+\frac{\mathrm{3}}{\mathrm{2}}\right]=\boldsymbol{{k}}\left(\boldsymbol{{x}}+\mathrm{1}\right) \\ $$$$\boldsymbol{{after}}\:\boldsymbol{{some}}\:\boldsymbol{{manipulation}}\:\boldsymbol{{you}}\:\boldsymbol{{get}} \\ $$$$\boldsymbol{{this}}\:\boldsymbol{{nice}}\:\boldsymbol{{result}}… \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{2}^{\boldsymbol{{n}}−\mathrm{1}} \int_{\mathrm{1}} ^{\frac{\mathrm{3}}{\mathrm{2}}} \frac{\left[\boldsymbol{{k}}−\mathrm{1}\right]^{\mathrm{2}\left(\boldsymbol{{n}}−\mathrm{1}\right)} }{\boldsymbol{{k}}^{\boldsymbol{{n}}} }\boldsymbol{{dk}} \\ $$$$\boldsymbol{{now}}\:\boldsymbol{{I}}_{\mathrm{2}} =\mathrm{2}\int_{\mathrm{1}} ^{\frac{\mathrm{3}}{\mathrm{2}}} \frac{\left(\boldsymbol{{k}}−\mathrm{1}\right)^{\mathrm{2}} }{\boldsymbol{{k}}^{\mathrm{2}} }\boldsymbol{{dk}}=\left[\frac{\mathrm{5}}{\mathrm{3}}−\mathrm{4}\boldsymbol{{ln}}\frac{\mathrm{3}}{\mathrm{2}}\right] \\ $$$$\boldsymbol{{and}}\:\boldsymbol{{I}}_{\mathrm{3}} =\mathrm{2}^{\mathrm{2}} \int_{\mathrm{1}} ^{\frac{\mathrm{3}}{\mathrm{2}}} \frac{\left(\boldsymbol{{k}}−\mathrm{1}\right)^{\mathrm{4}} }{\boldsymbol{{k}}^{\mathrm{3}} }\boldsymbol{{dk}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{4}\int_{\mathrm{1}} ^{\frac{\mathrm{3}}{\mathrm{2}}} \frac{\underset{\boldsymbol{{r}}=\mathrm{0}} {\overset{\mathrm{4}} {\sum}}\overset{\mathrm{4}} {\boldsymbol{{C}}}_{\boldsymbol{\mathrm{r}}} \boldsymbol{\mathrm{k}}^{\left(\mathrm{4}−\boldsymbol{\mathrm{r}}\right)} \left(−\mathrm{1}\right)^{\boldsymbol{\mathrm{r}}} }{\boldsymbol{\mathrm{k}}^{\mathrm{3}} }\boldsymbol{\mathrm{dk}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=−\frac{\mathrm{525}}{\mathrm{54}}+\mathrm{24}\boldsymbol{{ln}}\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\bigstar\boldsymbol{{very}}\:\boldsymbol{{lengthy}}\:\boldsymbol{{so}}\:\boldsymbol{{I}}\:\boldsymbol{{avoid}}\:\boldsymbol{{the}} \\ $$$$\boldsymbol{{total}}\:\boldsymbol{{calculation}}. \\ $$$$ \\ $$
